设A是n阶方阵，若存在n维非零向量x，使得：
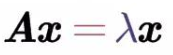
那么就称λ是A的特征值，x为A属于λ的特征向量，一个矩阵的一组特征向量是一组正交向量。
特征值分解是将一个矩阵分解成下面的形式：
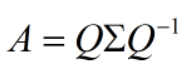
其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角阵，每一个对角线上的元素就是一个特征值。
首先要明确的是一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。比如说下面这个矩阵：
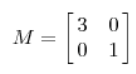
这个矩阵对应的线性变换为：
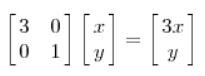
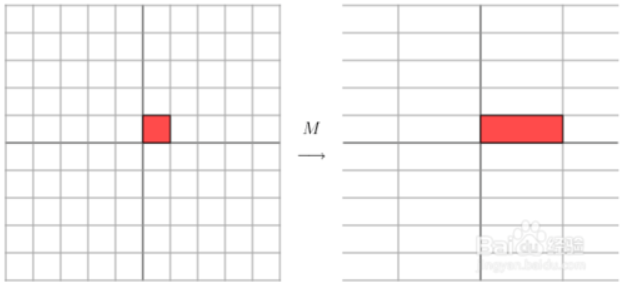
由于上面这个矩阵式对称的，所以变换是一个对x，y轴的方向一个拉伸变换（每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，是拉长，当值<1时时缩短），当矩阵不是对称的时候，假如说矩阵是下面的样子：
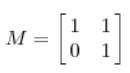
那么变换是：
其实就是在平面上对一个轴进行拉伸变换，蓝色的箭头是最主要的一个方向（变化的方向可能不止一个），如果想要描述好一个变换，那就描述这个主要的变化方向就好了。
特征值分解的式子里分解得到的对角阵，里面的特征值是从大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）。
当矩阵式高维时候，这个矩阵就是高维空间下的一个线性变换，这个变换同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变换方向。我们利用这N个变换方向，就可以近似这个矩阵变换。也就是说的：提取这个矩阵的最主要的特征。
总结：特征值分解可以得到特征值与特征向量，特征值表示这个特征有多重要，而特征向量表示这个特征向量是什么，可以将每个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多事情。特征值分解有很多的局限性，变换的矩阵必须是方阵。