
这篇文章的目的是介绍关于利用自动编码器实现图像降噪的内容。
在神经网络世界中,对图像数据进行建模需要特殊的方法。其中最著名的是卷积神经网络(CNN或ConvNet)或称为卷积自编码器。并非所有的读者都了解图像数据,那么我先简要介绍图像数据(如果你对这方面已经很清楚了,可以跳过)。然后,我会介绍标准神经网络。这个标准神经网络用于图像数据,比较简单。这解释了处理图像数据时为什么首选的是卷积自编码器。最重要的是,我将演示卷积自编码器如何减少图像噪声。这篇文章将用上Keras模块和MNIST数据。Keras用Python编写,并且能够在TensorFlow上运行,是高级的神经网络API。
了解图像数据
如图(A)所示,图像由“像素”组成。在黑白图像中,每个像素由0到255之间的数字表示。如今大多数图像使用24位彩色或更高的颜色。一幅RGB彩色图像表示一个像素的颜色由红色、绿色和蓝色组成,这三种颜色各自的像素值从0到255。RGB色彩生成器(如下所示)表明,RGB色彩系统利用红绿蓝,组合成各种颜色。因此,一个像素由含三个值的RGB(102、255、102)构成,其色号为#66ff66。

宽800像素,高600像素的图像具有800 x 600 = 480,000像素,即0.48兆像素(“兆像素”等于100万像素)。分辨率为1024×768的图像是一个由1,024列和768行构成的网格,共有1,024×768 = 0.78兆像素。
MNIST
MNIST数据库是一个大型的手写数字数据库,通常用于训练各种图像处理系统。Keras的训练数据集具备60,000条记录,而测试数据集则包含了10,000条记录。每条记录共有28 x 28个像素。
from keras.layers import Input, Dense
from keras.models import Model
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
它们看起来怎么样?我们用绘图库及其图像功能imshow()展示前十条记录。
import matplotlib.pyplot as plt
n = 10 # 显示的记录数
plt.figure(figsize=(20, 4))
for i in range(n):
# 显示原始图片
ax = plt.subplot(2, n, i 1)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

图像数据的堆叠,用于训练
如果要让神经网络框架适用于模型训练,我们可以在一列中堆叠所有28 x 28 = 784个值。第一条记录的堆叠列如下所示(使用x_train[1].reshape(1,784)):

然后,我们可以使用标准的神经网络训练模型,如图(B)所示。数值为784的每个值都是输入层中的一个节点。且慢!堆叠数据会丢失很多信息吗?答案是肯定的。图像中的空间关系被忽略了。这使得大量的信息丢失。那么,我们接着看卷积自编码器如何保留空间信息。

为什么图像数据首选卷积自编码器?
可以看到,数据切片和数据堆叠会导致信息大量丢失。卷积自编码器放弃堆叠数据,使图像数据输入时保持其空间信息不变,并在卷积层中以温和的方式提取信息。图(D)演示了将平面2D图像先提取到一个厚的正方体(Conv1),再提取到一个长方体(Conv2)和另一个长度更长的长方体(Conv3)。此过程旨在保留数据中的空间关系。这是自动编码器的编码过程。中间部分是一个完全连接的自动编码器,其隐藏层仅由10个神经元组成。然后就是解码过程。三个立方体将会展平,最后变成2D平面图像。图(D)的编码器和解码器是对称的。实际上,编码器和解码器不要求对称。

卷积自编码器如何工作?
上面的数据析取似乎很神奇。数据析取究竟是如何进行的?这包括以下三层:卷积层,线性整流层和池化层。
1. 卷积层
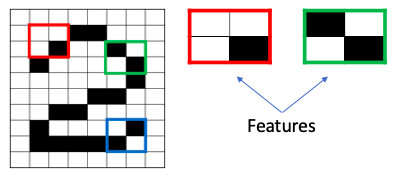
卷积步骤会生成很多小块,称为特征图或特征,如图(E)的绿色、红色或深蓝色的正方形。这些正方形保留了输入图像中像素之间的关系。如图(F)所示,每个特征扫描原始图像。这一产生分值的过程称为卷积。
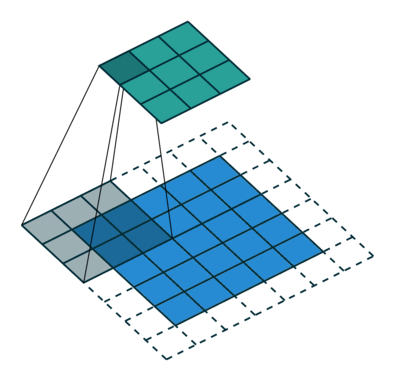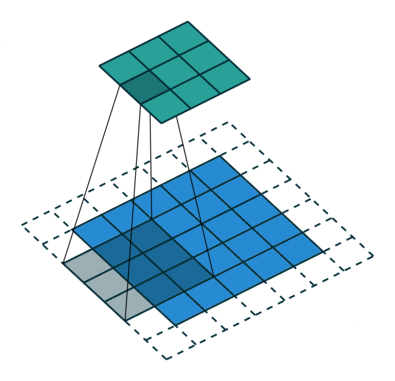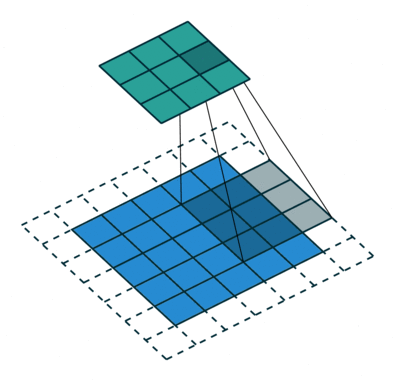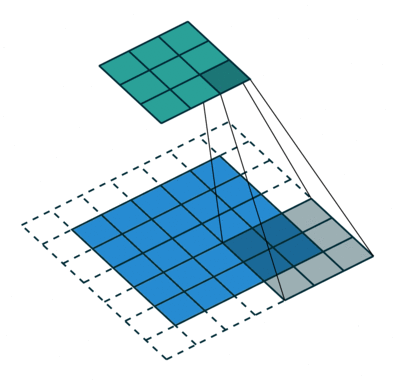
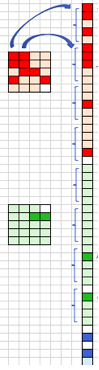
扫描完原始图像后,每个特征都会生成高分值和低分值的滤波图像,如图(G)所示。如果匹配完美,那块正方形的得分就高。如果匹配度低或不匹配,则得分低或为零。例如,原始图像有四个区域与红色方块完全匹配,那么这四个区域的得分都很高。

过滤器越多,模型可以提取的特征就越多。但是,特征越多,训练时间也就越长。因此,最好还是选择最少的过滤器提取特征。
1.1填充
特征如何确定匹配项?一种超参数是填充,有两种选择:(i)用零填充原始图像以符合该特征,或(ii)删除原始图像中不符的部分并保留有效部分。
1.2步长
卷积层的另一个参数:步长。步长是输入矩阵上移动的像素个数。当步长为1时,过滤器一次移动1个像素。在Keras代码中,我们将其视为超参数。
2.线性整流步骤
线性整流单位(ReLU)的步骤与典型的神经网络相同。它将所有的负值校正为零,确保数学运算正确。
3.最大池化层
池化会缩小图像尺寸。在图(H)中,一个2 x 2的窗口(称为池的大小)扫描每个滤波图像,并将该2 x 2窗口的最大值划分给新图像中大小为1 x 1的正方形。如图(H)所示,第一个2 x 2窗口的最大值分数高(用红色表示),因此高分划分给1 x 1正方形。

除了采用最大值之外,其他不常用的池化方法还包括“平均池化”(取平均值)或“总和池化”(总和)。
池化后,会生成新的更小的滤波图像。现在我们拆分这个滤波图像,然后堆叠为一列,如图(J)所示。
Keras模型
以上三层是卷积神经网络的构建块。Keras具有以下两个功能:
• Conv2D(filters, kernel_size, activation = ‘reLu’, strides=1):核尺寸(kernel_size)是2D卷积窗口的高度和宽度。图(E)使用的是2×2正方形,所以例子中核尺寸将为(2,2)。步长是输入矩阵上移动的像素个数。我们一次将滤镜移动了1个像素,所以步长为1。
• MaxPooling2D(pool_size=(2,2)):在图(H)中,我们使用2×2窗口作为池的大小。因此,我们将在以下代码中使用(2,2)。
你可以在卷积自编码器中构建许多卷积层。在图(E)中,在编码部分有三层,分别标记为Conv1,Conv2和Conv3。因此,我们要进行相应的构建。
• 下面的代码input_img = Input(shape=(28,28,1)表明输入的2D图像为28 x 28。
• 然后,它构建了Conv1,Conv2和Conv3。
• 请注意,Conv1在Conv2内部,而Conv2在Conv3内部。
• 要是过滤器无法适应输入图像,填充将指定下一步该做什么。padding='valid’表示过滤器不符合,图像的一部分将被丢弃;padding='same’用零填充图片以适应图片。
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
# 编码过程
input_img = Input(shape=(28, 28, 1))
############
# 编码 #
############
# Conv1 #
x = Conv2D(filters = 16, kernel_size = (3, 3), activation='relu', padding='same')(input_img)
x = MaxPooling2D(pool_size = (2, 2), padding='same')(x)
# Conv2 #
x = Conv2D(filters = 8, kernel_size = (3, 3), activation='relu', padding='same')(x)
x = MaxPooling2D(pool_size = (2, 2), padding='same')(x)
# Conv 3 #
x = Conv2D(filters = 8, (3, 3), activation='relu', padding='same')(x)
encoded = MaxPooling2D(pool_size = (2, 2), padding='same')(x)
# 注意:
# padding 是一个超参数,值'valid' or 'same'.
# "valid" 意味不需要填充
# "same" 填充输入,使输出具有与原始输入相同的长度。
然后,解码过程继续。因此,下面解码部分已全部完成编码和解码过程。
############
# 解码 #
############
# DeConv1
x = Conv2D(8, (3, 3), activation='relu', padding='same')(encoded)
x = UpSampling2D((2, 2))(x)
# DeConv2
x = Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = UpSampling2D((2, 2))(x)
# Deconv3
x = Conv2D(16, (3, 3), activation='relu')(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
该Keras API需要模型和优化方法的声明:
•• Model (inputs= input_img,outputs= decoded):在解码给定输入数据input_img的情况下,模型包括计算输出所需的所有层。compile(optimizer=‘adadelta’,loss=‘binary_crossentropy’):优化程序会像渐变梯度一样执行优化操作。最常见的是随机梯度下降(SGD),自适应梯度(Adagrad)和Adadelta(Adadelta是Adagrad的扩展)。有关详细信息,请参见Keras优化器文档。损失函数可以查找Keras损失文档。
# 声明模型
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy')
下面,我使用x_train作为输入和输出来训练模型。batch_size是样本量和epochs是迭代的次数。我指定shuffle=True打乱训练数据。
# 训练模型
autoencoder.fit(x_train, x_train,
epochs=100,
batch_size=128,
shuffle=True,
validation_data=(x_test, x_test)
)
我们可以打印出前十张原始图像和相同十张图像的预测。
decoded_imgs = autoencoder.predict(x_test)
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# 显示原始图像
ax = plt.subplot(2, n, i 1)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# 显示重构后的图像
ax = plt.subplot(2, n, i 1 n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

如何构建图像降噪卷积自编码器?
图像降噪的想法是训练一个模型,输入噪声数据,并输出它们各自清晰的数据。这是与上述模型的唯一区别。首先让我们向数据添加噪音。
noise_factor = 0.4
x_train_noisy = x_train noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape)
x_test_noisy = x_test noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
前十张噪声图像如下所示:
n = 10
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i 1)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

然后,我们训练模型时将输入噪声数据,输出干净的数据。
autoencoder.fit(x_train_noisy, x_train,
epochs=100,
batch_size=128,
shuffle=True,
validation_data=(x_test_noisy, x_test)
)
最后,我们打印出前十个噪点图像以及相应的降噪图像。
decoded_imgs = autoencoder.predict(x_test)
n = 10
plt.figure(figsize=(20, 4))
for i in range(n):
# 显示原始图像
ax = plt.subplot(2, n, i 1)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# 显示重构后的图像
ax = plt.subplot(2, n, i 1 n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

是否可以使用任何经过训练的CNN代码吗?
可以的。如果你有兴趣学习代码,Keras提供了几个经过预训练的CNN,包括Xception,VGG16,VGG19,ResNet50,InceptionV3,InceptionResNetV2,MobileNet,DenseNet,NASNet和MobileNetV2。值得一提的是,你可以出于研究目的付钱或下载此大型图像数据库ImageNet。
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/
欢迎关注PyTorch官方中文教程站:
http://pytorch.panchuang.net/
OpenCV中文官方文档:
http://woshicver.com/