- 简述
- 介绍
- 概述
- 总结
一.简述
本次翻译一篇Liu Wei的一篇论文,之前介绍谱聚类的时候大家都知道,用谱聚类对样本进行分割,大概的流程就是先将原始数据通过不同的规则构建出相似度矩阵,然后再用相似度矩阵表示拉普拉斯矩阵,再对拉普拉斯矩阵进行特征分解,取前k个最小的特征值对应的特征向量,这几个特征向量组成的矩阵每行表示样本,进行聚类。但是在大数据下,传统的方法构建的相似度矩阵,需要每个样本都与别的样本之间计算相似度,那这样构建高纬度的相似度矩阵会很耗时间。传统的构建相似度矩阵都是样本与样本之间计算得到的,本篇论文中Liu就提出了全新的基于样本与m个初始聚类中心的关系构建样本与m个聚类中心的相似度矩阵Z后,再构建样本与样本间的相似度矩阵W。
二.介绍
随着互联网的快速发展,现在我们能收集大量的无类标数据,比如图像,声音,接着对对高维度半监督学习的需求就上升了。不幸的是,大多数的半监督学习方法对高维度下的数据具有很差的适应性。比如,经典的TSVM在面对以指数增长的数据大小时,是具有很高的计算量的挑战的。在大量的TSVM不同版本中,CCCP-TSVM具有最低的复杂度,但是也至少需要O(n^2)的复杂度,所以也很难处理高维数据。
基于图构建的半监督学习(Graph-based SSL)近来得到大家的注意,因为它很容易实施并且得到封闭解的方法。然而自从n*n的图拉普拉斯矩阵的逆矩阵需要后,Graph-based SSL经常会有立方的时间复杂度O(n^3)。因此,阻碍了对真实生活中大量无类标问题的广泛应用。为了调和立方的时间复杂度,近来的学习是寻找降低对拉普拉斯矩阵操作的计算量。Delalleu在2005年提出了一个无参归纳的方法,该方法能让类标预测建立在样本的子集上,接着缩短了子集样本上的拉普拉斯矩阵跟剩余样本德联系。很明显,这样的缩短方法忽略了输入数据的主要部分的拓扑结构,由此,丢失了大量数据信息。Zhu&Lafferty在2005年对原生数据构建了一个生成混合模型,提出了harmonic mixtures来测量类标预测的方法,但是这个没有解释怎样构建一个像提出的harmonic mixtures一样的高维稀疏矩阵。
在这片paper中,我们提出了一个高维图构建方法来高效的利用所有样本点。这个方法是简单且可可升级的,享有线性空间复杂性,时间复杂度与数据尺寸相关。
三.概述
我们从两方面尝试解决与半监督学习相关的可扩展问题:基于中心点的类标预测(anchor-based label prediction),邻接矩阵即样本与样本间的相似度矩阵的设计(adjacency matrix design)。
3.1Anchor-Based Label Prediction
我们关键的观察点是来自全尺寸下样本预测模型的基于图的半监督学习计算的密集型。自从在高维度下应用的无类标样本的数量变得巨大了以后,学习一个全尺寸下的预测模型是很低效率的。假设一个类标预测函数f : R^d → R,定义在输入样本上X={X1,X2,…,Xn}。我们假设前l个样本是有类标的,其余的样本是无类标的。为了在高维数据下适用,Delalleu在2005年构建了一个预测函数,该函数是在其中一部分anchors下的样本类标的加权平均值。如果能够推出类标与小得多的anchors子集的联系,其他无类标的样本就能很容易从简单的线性组合中获得类标。
这个想法是用了一个子集,这其中每个Uk充当了一个anchor中心点,(这些点就是初始化的anchors聚类中心点),现在对于每个xi的预测函数f(xi),我们替换成m个uk点放入预测函数求和。
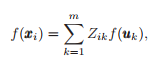
这里Z_ik是样本适应权重(代表Xi样本与Uk的关联强度),这样的类标预测高效的进行无参的回归。让我们定义两个向量
![]()
重新写公式一:
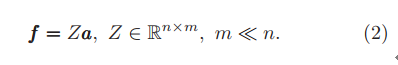
这个公式提供了一个可扩展半监督学习的主要处理方法,因为它减少了无类标的解空间,从很大的f(n*1)到小的多的a(m*1)。这种高效的类标预测模型确实缓和了最初全尺寸模型的计算负担。
重要的是,我们使用Kmeans聚类中心代替随机取某些样本来表示这些anchor点{Uk}。因为使用kmeans聚类中心会有一个更好的充分覆盖,得到的聚类中心会更加均匀。
3.2邻接矩阵的设计
假设存在由n个数据点构建一个无向图G(V,E,W),V是图的节点,代表n个数据点,Vi代表Xi,E(V*V的维度)是边的集合,代表邻接矩阵的中的点,W是一个加权的邻接矩阵,该W测量边的长度。显然,图中的边连接是很重要的,一个广泛使用的连接策略是基于KNN原则构建图,当Xi是Xj最近的几个相邻点或者反之亦然时,KNN图会创造一条边来表示他两之间的联系。基于KNN原则构建图的时间复杂度为O(kn^2),所以传统的基于KNN原则构建的图在大尺度数据下是不可行的。即使我们或许能构造一个近似KNN原则构建的图来节省点时间,在涉及到操作高维图时,大矩阵的求逆或者大尺寸的线性求解仍然是一个大的障碍。
3.3设计原则
现在我们研究了一些指定高维度问题下设计Z和W的一些原则。
原则1
![]()
邻近的数据应该拥有相似的类标,相隔很远的数据应该类标很不相同。这使得我们也对Zik同样施加了影响,当Uk离Xi很远时,Zik=0.最终我们会得到一个稀疏非负的矩阵Z(n*m维度)
原则2
我们需要W>=0,非负的邻接矩阵能充分让得到的拉普拉斯矩阵L=D-W正定,该理论已经由Chuang在1997年证明了。这个非负的性质对确保得到很多基于图的半监督学习得到全局最优解很重要。
原则3
我们更想要一个稀疏矩阵W,因为稀疏矩阵能在不相似的点之间有更少的无用连接,这样的稀疏矩阵W会倾向于有更高的质量。Zhu在2008年已经指出稠密矩阵相比于稀疏矩阵会表现的更差。
直观的,我们会用一个非负的稀疏矩阵Z去设计非负稀疏矩阵W。实际上,在下一部分,我们会共同设计Z和W,产生一个经验上稀疏的高维度图。相反地,最近Zhang在2009年提出的Prototype Vector Machine (PVM),分开设计Z和W,产生了不适当的密集型图,除此之外,当使用Nystrom方法时,PVM未能保证图相邻矩阵的非负性。因此,PVM不能保证图拉普拉斯的时间消耗是收敛的。因此,我们直接设计W,确保它非负和稀疏的特性。
四.总结
本篇论文先翻译到这里,在这里我们发现了,在处理高维度数据时,传统的方法都因为很高的时间复杂度,而难以驾驭得了高维度数据处理问题。大家都在找原来样本与样本之间的相似矩阵W的近似表达。近期人们提出了样本与初始聚类的关系构建了相似度矩阵Z,想通过Z构建邻接矩阵也就是相似度矩阵W,这样的话,本来求W(n*n)的问题就会被转换成Z(n*m)的问题,m<<n,这就为我们在处理高维度数据上带来了可能。下次会着重讲解如何构建Z和W。