|
具体代码可以在我码云里获得:https://gitee.com/wu_ji666/mpi_Eratosthenes.git 一.步骤及操作: 1.1, VS2017上MPI的安装和配置: 1.1.1安装: a.mpi官方下载地址:http://www.mpich.org/downloads/,下载后按照安装指导操作即可 1.1.2配置: 配置具体步骤(每次新建mpi工程时都要重新对工程进行配置): 右击项目-->>属性,进行配置: 右上角-->>配置管理器-->>活动解决方案平台,选择:x86(我是64位系统,如果是32位,选择x64); VC++目录-->>包含目录,添加:“D:Program Files (x86)Microsoft SDKsMPIInclude;” VC++目录-->>库目录,添加:“D:Program Files (x86)Microsoft SDKsMPILibx64;” C/C++ -->> 预处理器-->>预处理器定义,添加:“MPICH_SKIP_MPICXX;” C/C++ -->> 代码生成 -->> 运行库,选择:多线程调试(/MTd); 链接器 -->> 输入 -->> 附加依赖项,添加:“msmpi.lib;” 1.1.3调试: 1 #include<stdio.h> 2 3 #include<mpi.h> 4 5 int main(int argc, char *argv[]) { 6 7 int myid, numprocs; 8 9 MPI_Init(&argc,&argv); 10 11 MPI_Comm_rank(MPI_COMM_WORLD, &myid); 12 13 MPI_Comm_size(MPI_COMM_WORLD, &numprocs); 14 15 16 17 printf("%d Hello world from process %d ",numprocs, myid); 18 19 20 21 MPI_Finalize(); 22 23 return 0; 24 25 } 对这段代码编译并生成exe,用命令行执行mpiexec得到: 图1.1.1 表明成功!
1.2, 埃拉托斯特尼筛法基准代码调试: 1.2.1. 关键代码 就是基准代码,做了一些修改: a.加入#include <stdlib.h> b.int改为long long int c.加入结果写入文件模块(其他优化代码里一直沿用): 1 void write_txtfile(double k, int num_pro, long long int num) 2 3 { 4 5 FILE * pFile = fopen("E:/VS_pro/文件名", "a+"); 6 7 8 9 if (NULL == pFile) 10 11 { 12 13 printf("error"); 14 15 return; 16 17 } 18 19 fprintf(pFile, "Thread num:%d,Arrange:%lld, Time:%10.6f ", num_pro, num, k); 20 21 fclose(pFile); 22 23 return; 24 25 } 1.3. 埃拉托斯特尼筛法去偶数优化: 1.3.1. 思想和方法: 利用“大于2的质数都是奇数”这一知识,首先去掉所有偶数,偶数必然不是素数,这样相当于所需要筛选的数减少了一半,存储和计算性能都得到提高。 1.3.2. 关键代码
int N = (n - 1) / 2;//just half of all low_value = (id * (N / p) + MIN(id, N % p)) * 2 + 3; //irst ele. in this pross. high_value = ((id + 1) * (N / p) + MIN(id + 1, N % p)) * 2 + 1;//last ele... size = (high_value - low_value) / 2 + 1; //the size in this pross... …… // marked all for (int i = 0; i < size; i++) marked[i] = 0; if (!id) index = 0; prime = 3; do { if (prime * prime > low_value) { first = (prime * prime - low_value) / 2; } else { if (!(low_value % prime)) first = 0; //kicked out the even else if (low_value % prime % 2 == 0) first = prime - ((low_value % prime) / 2); else first = (prime - (low_value % prime)) / 2; } …… if (!id) { while (marked[++index]); prime = index * 2 + 3; // start of 3 } 事实上,去偶数重要的是索引的确定! 1.4. 埃拉托斯特尼筛法消除广播: 1.4.1 思想和方法 基准代码是通过进程0广播下一个筛选倍数的素数。进程之间需要通过MPI_Bcast函数进行通信。通信就一定会有开销,因此我们让每个进程都各自找出它们的前sqrt(n)个数中的素数,在通过这些素数筛选剩下的素数,这样一来进程之间就不需要每个循环广播素数了,性能得到提高。 1.4.2关键代码 1 /* 2 3 广播优化 4 5 */ 6 7 //先找前sqrt(n)内的素数,再通过这些素数筛选后续素数 8 9 int sqrt_N = (((int)sqrt((double)n)) - 1) / 2; 10 11 12 13 low_NewArray_value = MIN(0, sqrt_N % p) * 2 + 3; //first ele. in this pross.(in NewArray) 14 15 high_NewArray_value = ((sqrt_N / p) + MIN(1, sqrt_N % p)) * 2 + 1;//last ele...(in NewArray) 16 17 18 19 // Bail out if all the primes used for sieving are not all held by process 0 20 21 proc0_size = (sqrt_N - 1) / p; 22 23 24 25 if ((2 + proc0_size) < (int)sqrt((double)sqrt_N)) { 26 27 if (!id) printf("Too many processes "); 28 29 MPI_Finalize(); 30 31 exit(1); 32 33 } 34 35 36 37 NewMarked = (char *)malloc(sqrt_N); 38 39 if (NewMarked == NULL) { 40 41 printf("Cannot allocate enough memory "); 42 43 MPI_Finalize(); 44 45 exit(1); 46 47 } 48 49 50 51 //all ele. in NewArray was be marked 52 53 for (int i = 0; i < sqrt_N; i++) 54 55 NewMarked[i] = 0; 56 57 58 59 index = 0; 60 61 62 63 prime = 3; 64 65 do { 66 67 first = (prime * prime - low_NewArray_value) / 2; 68 69 70 71 // 该素数的倍数排除 72 73 for (int i = first; i < sqrt_N; i += prime) { 74 75 NewMarked[i] = 1; 76 77 } 78 79 80 81 while (NewMarked[++index]); 82 83 prime = index * 2 + 3; 84 85 86 87 } while (prime * prime <= sqrt_N); 88 89
1.5. 埃拉托斯特尼筛法cache优化: 1.5.1. 思想和方法: (0)Cache配置如图: 图1.5.1 (1)已知Cache是以CacheLine大小为单位交换数据的,考虑到CacheLine共用时的伪共享问题,首先进行Cacheline对齐,使每一个线程需要的数据在不同的Cacheline。我的电脑Cache配置已知CacheLine大小为64B,那么我们设置新的数据结构来完成数据Cacheline对齐:;并计算每个处理器占有的Cacheline数; (2)考虑到Cache整体与内存的交换行为,我们进行分块。已知三级缓存为6M(之所以用三级缓存是为了避免L2L1级缓存太小导致Cache命中率过低,反而降低优化性能)。在已知每个处理器占有的CacheLine数基础上,把这些CacheLIne集中成块。 列如:每个处理器可以获得的Cache大小为:Cache大小/核心数 占有CacheLIne数为:每个处理器可以获得的Cache大小/数据结构占有空间大小 1.5.2. 关键代码 代码注释详细,思路可见一斑。 1 int Cache_linenum_pro = CACHE_SIZE / (CACHELINE_SIZE*p);//每个进程占有的cacheline 2 3 int CacheBlock_size = Cache_linenum_pro * 8;//每个进程获得的用于存取long long的块大小 4 5 int Block_N = CacheBlock_size - 1; 6 7 int line_need = size / CacheBlock_size;//每个进程一共需要多少块 8 9 int line_rest = size % CacheBlock_size;//多出来的cacheline 10 11 int time_UseCache = 0; 12 13 14 15 16 17 // allocate this process 's share of the array 18 19 marked = (char *)malloc(CacheBlock_size); 20 21 if (marked == NULL) { 22 23 printf("Cannot allocate enough memory "); 24 25 MPI_Finalize(); 26 27 exit(1); 28 29 } 30 31 32 33 //就是块内去除偶数的判定过程 34 35 count = 0; 36 37 38 39 while (time_UseCache <= line_need) { 40 41 42 43 //cache更新; 44 45 Block_pos_last.value = (time_UseCache + 1) * Block_N + MIN(time_UseCache + 1, line_rest) - 1 + (id * (N / p) + MIN(id, N % p)); 46 47 Block_pos_first.value = time_UseCache * Block_N + MIN(time_UseCache, line_rest) + (id * (N / p) + MIN(id, N % p)); 48 49 Block_low_value.value = Block_pos_first.value * 2 + 3; 50 51 if (time_UseCache == line_need) { 52 53 Block_high_value.value = high_value; 54 55 Block_pos_last.value = (id + 1) * (N / p) + MIN(id + 1, N % p) - 1; 56 57 CacheBlock_size = ((Block_high_value.value - Block_low_value.value) >> 1) + 1; 58 59 } 60 61 else { 62 63 Block_high_value.value = (Block_pos_last.value + 1) * 2 + 1; 64 65 } 66 67 68 69 70 71 index = 0; 72 73 prime.value = 3; 74 75 count_cacheBlock = 0; 76 77 78 79 for (int i = 0; i < CacheBlock_size; i++) marked[i] = 0; 80 81 82 83 // 块内素数 84 85 do { 86 87 if (prime.value * prime.value > Block_low_value.value) { 88 89 first.value = (prime.value * prime.value - Block_low_value.value) >> 1; 90 91 } 92 93 else { 94 95 if (!(Block_low_value.value % prime.value)) first.value = 0; 96 97 else if (Block_low_value.value % prime.value % 2 == 0) first.value = prime.value - ((Block_low_value.value % prime.value) >> 1); 98 99 else first.value = (prime.value - (Block_low_value.value % prime.value)) >> 1; 100 101 } 102 103 for (int i = first.value; i < CacheBlock_size; i += prime.value) { 104 105 marked[i] = 1; 106 107 } 108 109 while (NewMarked[++index]); 110 111 112 113 114 115 prime.value = index * 2 + 3; 116 117 } while (prime.value * prime.value <= Block_high_value.value); 118 119 120 121 122 123 // 块内计数 124 125 for (int i = 0; i < CacheBlock_size; i++) { 126 127 if (marked[i] == 0) { 128 129 count_cacheBlock++; 130 131 } 132 133 } 134 135 136 137 //all blockes togather 138 139 count += count_cacheBlock; 140 141 // 处理下一个块 142 143 time_UseCache++; 144 145 } 146 147 |
|
二、实验数据及结果分析: 2.1 实验结果 2.1.1.正确性展示(部分): a.1e8:共5761455个素数; 1e8结果 b, 1e9:共50847534个素数;
1e9结果 c, 1e10:共105097565个素数。
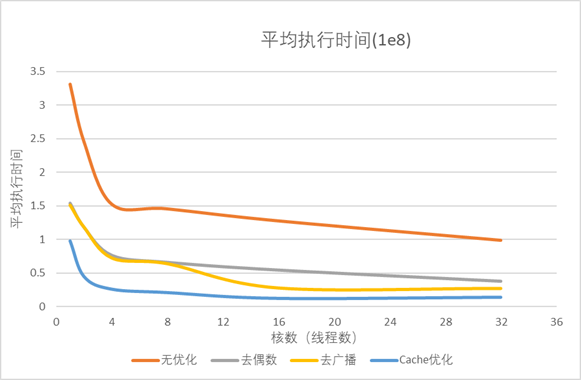
1e10结果 2.1.2.结果评价: a.1e8 执行时间:
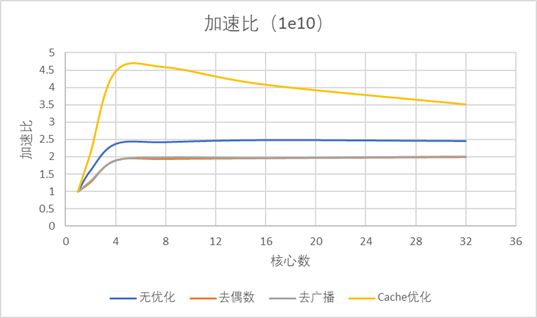
图2.1.1 图2.1.1中可以看到在1-16个核心数范围内,所有程序的执行时间都下降明显,当核心数超过16后,执行时间逐渐平缓。 加速比图: 图2.1.2 图2.1.2(加速比图中)易于发现,去偶数与原基准程序成线性,而去广播和Cache优化则在核心数16左右达到做大,之后趋于平缓。 并行效率图:
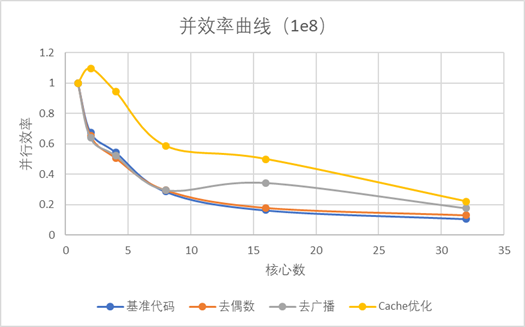
图2.1.3 图中显示了所有加速程序并行效率都随着核心数增加而下降;并且去偶数优化和基准程序基本一致,Cache优化并行效率同等核心数处于最高,去广播优化前期与基准程序一致,随着核心数增大,其并行效率明显高于基准程序。 纵比加速图: 同核心数下各优化方式相对于基准代码的加速效果:
图2.1.4 可以看出去偶数相较于基准程序加速比接近2倍,去广播可接近4倍,Cache优化效果最好,在核心数16时达到最大加速倍数为10-11倍;其中去偶数优化优化效果可以看做常数2,去广播和Cache优化则成峰分布,在16核心数左右达到最大。
b. 在此将数据扩大到1e10: 执行时间:
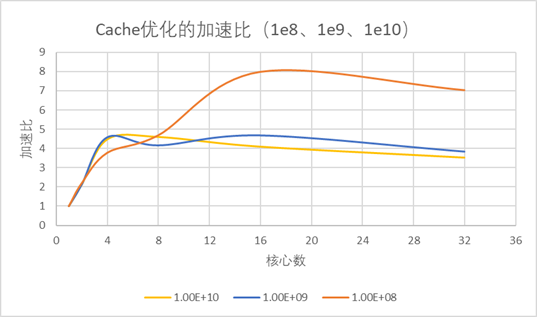
图2.1.5、 结果特征与1e8时一致。 加速比图: 图2.1.6 有趣的是,在1e8时加速比最大出现在16核心数,在1e10则为8;同时线性的特征消失(无论是基准程序还是去偶数)。 阿姆达尔效应验证: 图2.1.7 这个就更有趣了,按照阿姆达尔效应,随着问题规模增加,同一并行算法的加速比应该上升,然而结果是1e8的加速比遥遥领先,而1e9和1e10则比较接近。 2.1.3. 结果分析: (1).去偶数优化其实只是数量上线性的减少了问题规模(接近一半),通信和广播模式没有改变,所有优化效果是线性,接近2倍,并行效率也相似; (2).核心数少时广播代价并不大,随着核心数增加广播代价增大,所以在核心数很大时去广播优化就明显优于去偶数。 (3).显然存在计算代价、通信代价(或者广播代价、计算代价、通信代价),而通信(通信和广播)会随着核心数增加增大,所以Cache优化和去广播优化在加速计算时,如果通信代价过大,计算加速带来的收益就下降,加速比曲线存在峰;而通信代价与直接计算代价的相对比例在不同问题规模不同,使不同问题规模下最大加速比对应核心数不同; (4).通信代价存在,导致并行效率随核心数增大而下降; (5).问题规模溢出本人计算机性能,出现大规模加速比下降,反阿姆达尔效应。 |