北京航空航天大学2019年OO课程第一次总结
这是我大学近三年以来第一次正式地使用java编写程序,作为一名计算机专业的学生这似乎有点难以启齿。不过既然如此,更应当认真总结思考,有所收获和进步。俗话说的好,学习一门语言最好的时间就是十年前和现在(雾)。
一、第一、二次作业回顾
前两次作业要求实现一个简单函数的求导器。不难想象主控函数的功能就是负责读入、分析字符串并输出要求的运算结果。由于第一次作业是第二次作业的子集,接下来主要以第二次作业为例讨论。
问题可以分为3个部分:输入字符串的识别和处理、函数的程序表示与基本操作、函数的字符串表达。这三个问题也是三次作业的核心问题,理清问题层次对程序设计至关重要。接下来就对三个层次逐步分析,如何针对这些问题设计类与方法。
1.1 输入字符串处理
输入字符串可以分为普通表示和省略表示两种情况。利用编译原理的知识,我们可以将输入抽象为语言,该语言的文法如下(为了表示方便没有使用扩展BNF表示法):
<expr> => ([+-]?<term>)([+-]<term>)*
<term> => <factor>('*'<factor>)*
<factor> => <sinFactor>|<cosFactor>|<constant>|<powerFactor>
对于各个因子的具体表示比较简单,故略。那么,为什么要对输入字符串进行语法分析?我认为,这是将复杂问题简单化,明确思考对象和问题对象的重要方法。通过写出文法,现在可以很容易的将问题拆分为几个层次:将表达式拆分为项的集合;将项拆分为因子的集合;识别因子的种类并分析。同时,省略表示的问题也可以分层次解决——识别表达式层省略的首项符号和因子层省略的常数因子。
接下来的问题就很简单了,写出不同成分的正则表达式,利用正则表达式提取字符串后,再调用相应的分析函数,就可以为输入构造一个表达式对象。不同的函数只需考虑本层的问题,例如表达式层只需提取出项,同时识别省略格式,而无需关心项具体是怎样分析构造的。
1.2 函数的程序表示和操作
程序该怎样表示一个函数?一个函数应当具备哪些结构和功能?怎样设计函数类才能使得函数能很好的实现数学计算中的主要功能?这些都是设计函数类的重要问题。第二次作业中,对函数的要求只有求导。不难看出函数可以表示为形如下式的项的集合:
从数学的角度讲,作业范围中的函数全体构成了定义在上述集合下的阿贝尔群,该群包括可交换的加法运算和封闭的一元求导运算。求导运算是封闭的,因为:
更严谨的形式证明限于篇幅不在此赘述。总之,上述思考启发我们,一个项可以由唯一的四元组((a,b,c,d))表示,一个表达式可以由若干个项构成,这样就知道了类的设计。
对于表达式类,成员变量主要为项的数组(Array List),主要操作为求导——其本质上就是按照公式创建新的项并加入到新的表达式中。对于项类,成员属性即四个大数,分别对应决定参数。如果考虑优化,表达式类还应包含化简自己的方法。
1.3 表达式输出
输出思路较为简单,逐一输出项的各个成分即可,同时要注意判断能省略的情况。应当指出,打印字符串的语句(System.out.print)不应在输出方法中,更合适的做法是重载Object类的toString()方法,这样可以和编译器的Debug工具耦合起来,方便直接在不同环境下直接查看编译器自动显示的字符串。
二、第三次作业回顾
第三次作业和第一次类似,也从三个角度入手:
2.1 输入字符串处理
类似,第三次作业的语言的文法如下:
<expr> => ([+-]?<term>)([+-]<term>)*
<term> => <factor>((*)<factor>)*
<factor> => <sinFactor>|<cosFactor>|<constant>|<powerFactor>|<exprFactor>
<exprFactor> => '('<expr>')'
<sinFactor> => sin'('<factor>')'^<constant>
<cosFactor> => cos'('<factor>')'^<constant>
常数和指数因子的具体表示比较简单,故略。应当注意到,本次文法出现了递归的情况,包括表达式因子和三角函数因子。这使得无法使用一个普遍的正则表达式表示各个语法成分。因此,对于字符串的处理会变得更加复杂。这里我采用括号匹配的方式按层次分析语法成分,每次递归分析的都是最外层括号内的内容。例如sin(cos(x))这样的式子,我会屏蔽掉cos(x),只关心sin(...)这样的外部形式,对于里面的内容,就按照文法交给因子的处理程序,表达式因子也类似。
2.2 函数的程序表示和操作
由于没有了统一的表示形式,每个类的设计都变得更加抽象化。但是我们仍可以从文法入手去构造,对于常数和指数因子,其成员属性都是一个大数。除此之外,其他类的成员都是递归形式定义的。例如,表达式因子类包含一个表达式对象(表达式类和表达式因子类是不同的类),三角函数类包含一个因子对象和一个大数。同时,为了方便管理,可以将各个因子类全部继承于统一的父类Factor,他们用不同的方法重写父类的求导方法。
如果所有的类都提供求导的方法,那么求导的过程自然而然也可以递归进行。
现在,可以总结各个类的方法和属性了(子类只说明独有的部分):
| 表达式类 | 项类 | 因子类 | 三角函数因子类 | 表达式因子类 | 指数因子类 | |
|---|---|---|---|---|---|---|
| 主要成员 | 项对象数组 | 因子对象数组 | 因子类型,指数 | (三角内)因子对象 | 表达式对象 | - |
| 求导结果 | 表达式对象 | 项对象数组 | 因子对象数组 | - | - | - |
项的求导结果是若干个项,例如((f(x)*g(x))'=f'(x)g(x)+g'(x)f(x))。因子的求导结果是若干个因子,例如(sin(f(x))'=cos(f(x))*f'(x)),((f(x))'=(f(x)'))。构造一个语法对象,既可以通过参数构造,也可以通过字符串构造。
2.3 表达式输出
如果为每个类编写toString(),则任意语法成分均可以以递归的形式转化为字符串,这时,不同层次的语法对象需要关注的省略情况不同。项对象需要考虑常数的不同情况,表达式对象需要考虑符号的省略等等。更进一步的结构优化见后文。
三、基于度量的程序结构分析
使用IDEA的UML插件和代码分析工具DesigniteJava分析第三次作业,得到如下结果:
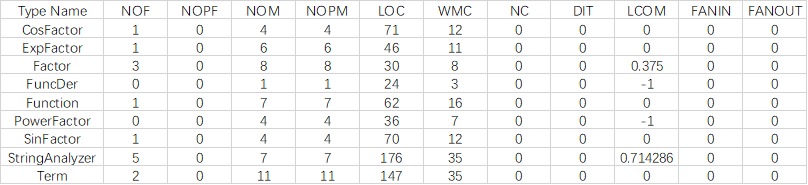
代码长度最长的是StringAnalyzer和Term,因为前者要为所有其他类提供字符串分析服务,包括括号匹配等,后者要实现较为复杂的优化。总的来说各个类方法数量和规模控制的还算合理。
对于类内聚合度评价指标LCOM,大部分值都很合理,StringAnalyzer类的值异常的高,说明该类不够满足内聚性,这是因为作为工具类大部分函数都是为其调用者提供的,内部并无逻辑关联。现在仔细思考,应当把其中方法全部设为静态类,并把代码都封装在同一个包里。另外,我的扇入扇出值均为0,这应该是程序的BUG,导致我很难分析耦合情况。不过从后文的类图可以看到,耦合度还是不错的,有几个模块被大量调用,而大部分模块都很少多次调用其他模块。

对于方法来说,53个方法只有一个圈复杂度超过了10,这是因为我的一个优化方法集成了太多不同类型的优化,应当分为不同的子方法,再使用父方法统一管理。除此之外大部分方法的性能都是令人满意的。
第三次作业的类图如下:
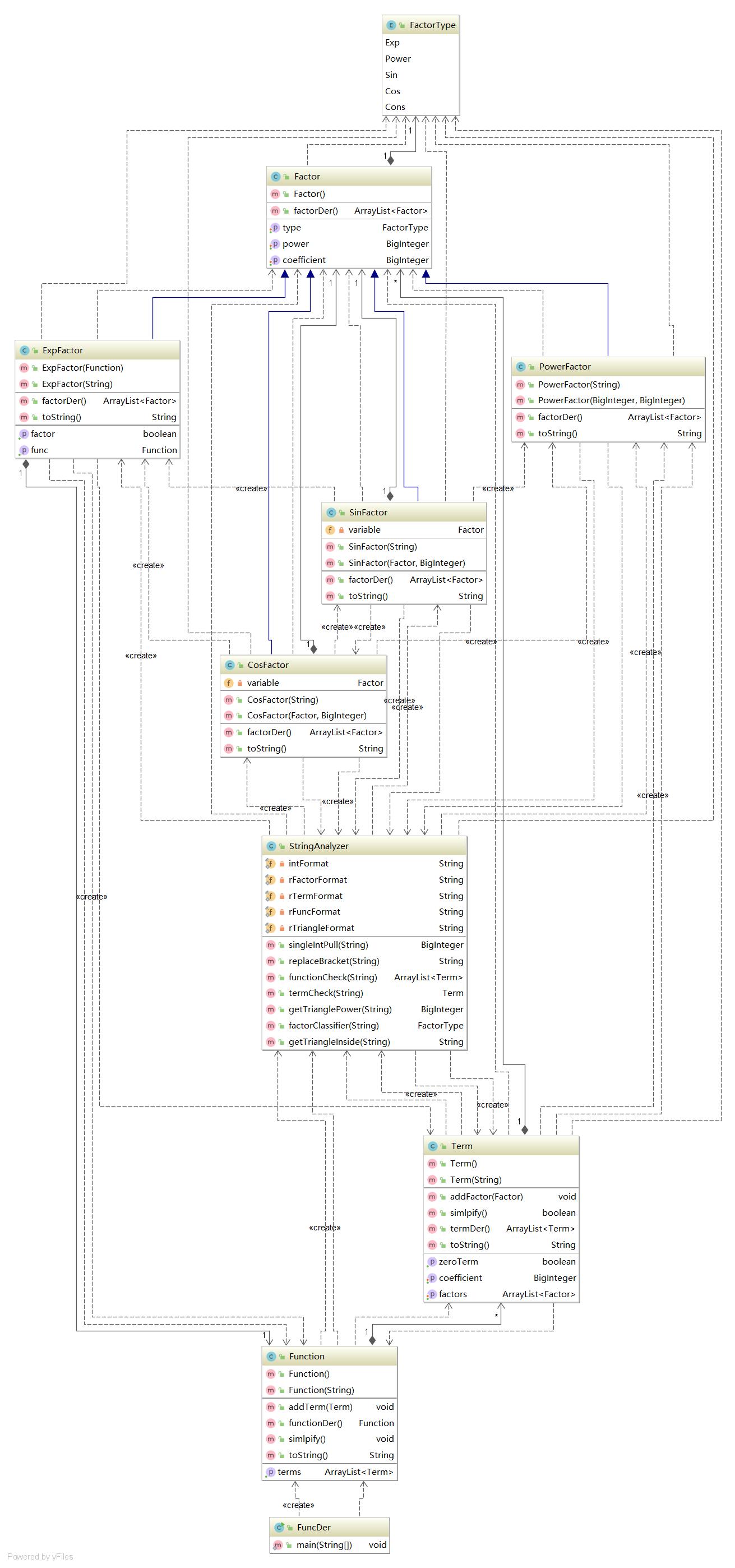
四、BUG的分析与改进
为了减少BUG、提高正确性,我从手动和自动两个角度进行调试。手动部分主要针对简单的分类和边界测试。分类测试中需要设计输入分类树,树的分叉点包括各个项的有无、省略形式输入等等。边界测试主要为难以想到的情况和极端情况,例如空输入、v符号、0次项等等。
自动测试主要使用python的自动化正则表达式生成器、subprocess指令和科学函数计算包,这样可以自动进行强度测试,测试点的深度和长度都可以自定义。虽然随机生成测试点质量可能不高,但是数量足够多时也可以提高 程序的可靠性。
由于我们没有互测,虽然从头到尾都没有发现结构性BUG(笔误等等不包含),本轮作业确实很难放心地说毫无BUG、或者基本没有BUG。然而,我们大家线下也有积极讨论、共享测试等等,这对于程序的精进起到了很大帮助。
五、使用对象创建模式
创建型模式是三大设计模式(创建型模式、结构型模式、工厂型模式)之一,另外两种为结构型模式与行为型模式。创建型模式一共分为五种模式:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。
工厂模式应该是适合本次作业的一种模式。若要使用工厂模式,则代码结构需要重构。对于Factor,可以按照如下思路重构:
抽象产品类Factor:
public interface Factor{
void factorDer();
}
定义实际产品类:
public class PowerFactor implements Factor{
...
@Override
public class PowerFactor(){
...
}
...
}
public class SinFactor implements Factor{
...
@Override
public class SinFactor(){
...
}
...
}
...
抽象的工厂接口:
public interface FactorFactory{
Factor getFactor();
}
具体工厂子类:
public class PowerFactorFactory implements FactorFactory{
@Override
public Factor getFactor(){
return new PowerFactor();
}
}
public class SinFactorFactory implements FactorFactory{
@Override
public Factor getFactor(){
return new SinFactor();
}
}
...
更多
关于优化思路,主要包括同类项合并和去除多余括号。对于去括号,主要思路在于展开表达式因子,如果表达式因子中的表达式只有一项,则表达式因子可以拆开合并入该因子所在的项中。另外,对于三角函数中的表达式因子,如果表达式因子本身就是一个因子,则输出时可以不加括号。