关于图表的理解

箱形图 

优点:  不受异常值的影响, 可以以一种相对稳定的方式描述数据的离散分布情况

用于反映一组或多组连续型定量数据分布的中心位置和散布范围。

1. 中位数 
   • 　二分之一分位数
   • n为奇数 (n+1) /2  , 如果n为偶数，n/2  (n/2)-1  这两个位置的数求平均值。
2. 上四分位数Q1
   •  该样本中所有数值由小到大排列后第25%的数字。
3. 下四分位数Q3
   • 　　该样本中所有数值由小到大排列后第75%的数字。
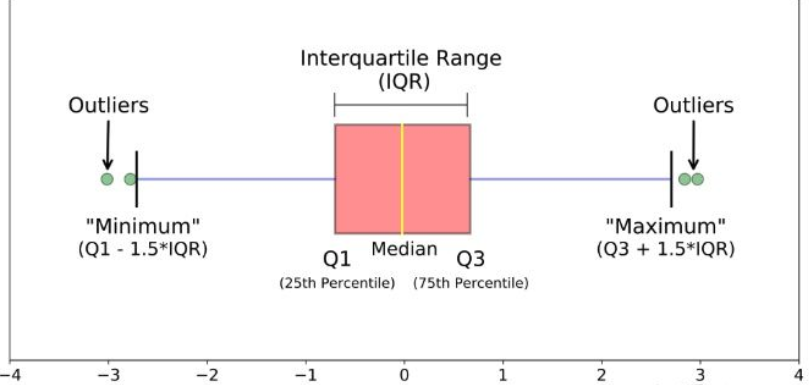
   • Q3-Q1的差距又称四分位距（InterQuartile Range）简称IQR
4. 上限
   • 　　非异常范围内的最大值。
   •  最大值区间Q3+1.5IQR  ,   最小值区间Q1-1.5IQR 
5. 下限 
   • 　　非异常范围内的最小值。
   •     Q1-1.5IQR

 上限与下限的距离， 称为 内限。

 还有一个外限，它的 最大值区间Q3+3IQR ， 最小值区间Q1-3IQR 。

　　　　内线之外，外限之内，属于中度异常。

　　　　外限之外，属极度异常。

 

---

连续型数据：在一定区间内可以任意取值的变量叫连续变量，其数值是连续不断的。例如，生产零件的规格尺寸，人体测量的身高、体重等，其数值只能用测量或计量的方法取得。可视化这类数据的图表主要有箱形图和直方图。

离散型数据：数值只能用自然数或整数单位计算的则为离散变量。例如，企业个数，职工人数，设备台数等，只能按计量单位数计数，数值一般用计数方法取得。大多数图表可视化的都是这类数据，比如柱状图、折线图等。

偏态

与正态分布相对，指的是非对称分布的偏斜状态。在统计学上，众数和平均数之差可作为分配偏态的指标之一：如平均数大于众数，称为正偏态（或右偏态）；相反，则称为负偏态（或左偏态）。