二叉树
树的定义
树是一种数据结构,它是由 n(n>=1)个有限节点组成的一个具有层次关系的集合。

树的特点:
- 每个节点有零个或多个字节点。
- 没有父节点的节点称为根节点。
- 每一个非根节点有且只有一个父节点。
- 除了根节点外,每个子节点可以分为多个不相交的子树。
节点的度:拥有子树的树目。
叶子节点:度为零的节点(没有子树)。
分支节点: 树中节点最大的度。
层次:树中节点的最大的度。
树的高度:树中节点的最大层次。
二叉树
二叉树是每个节点最多有两个子树的树结构。

-
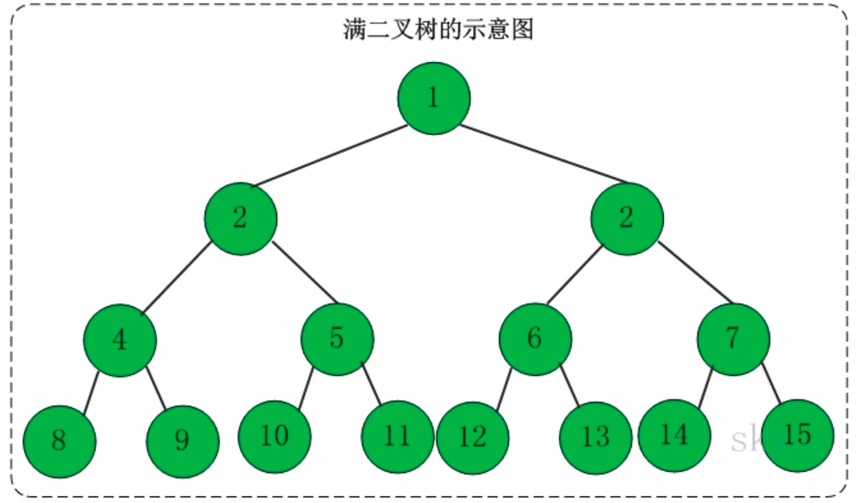
满二叉树
直观的说,除了叶子节点之外,所有的节点都有两个子节点。
-
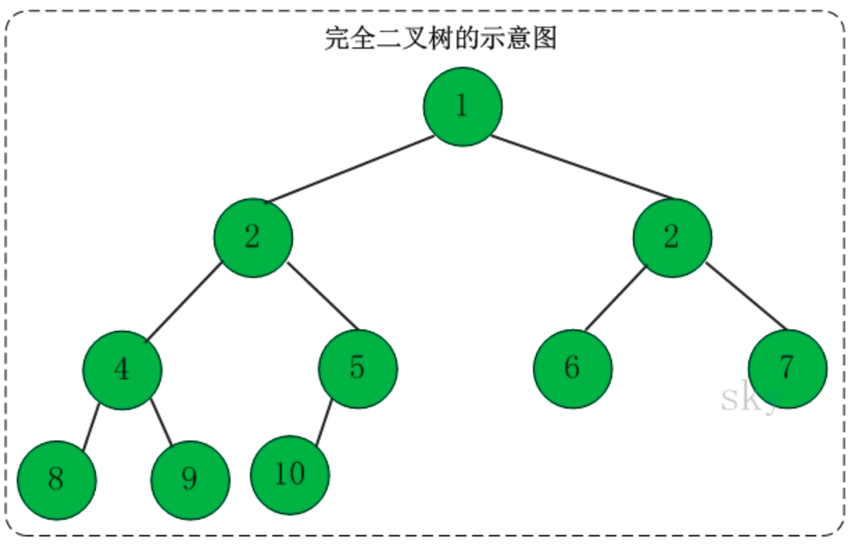
完全二叉树
一颗二叉树中,只有最下面两层节点的度可以小于2,并且最下层的叶子节点几种在靠左的位置上,这样的二叉树称为完全二叉树。
-
平衡二叉树
平衡二叉树要求它的左右子树的高度不超过 1, 并且左右子树都是一颗平衡二叉树。
如何判断一颗二叉树是不是平衡二叉树?
- 可以使用前序遍历的思想。先求出左右子树的高度,判断它们的高度差是否超过了 1。
- 递归判断左子树。
- 递归判断右子树。
-
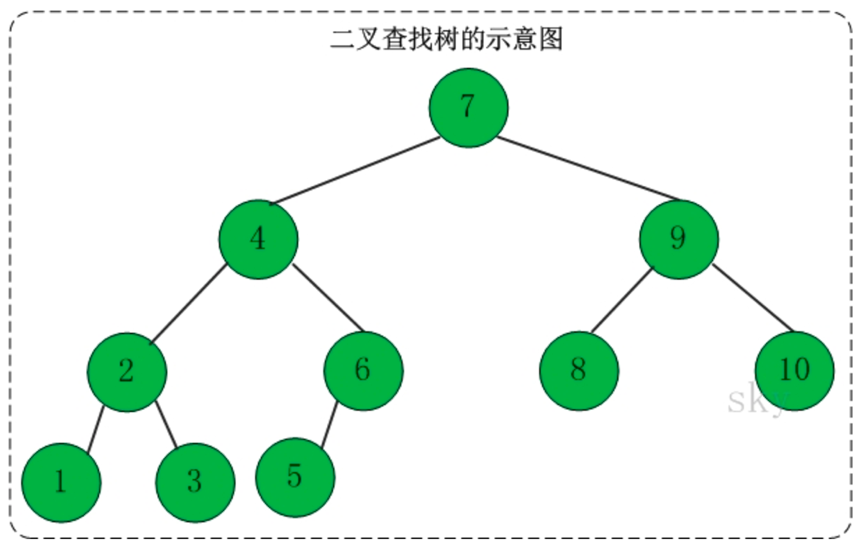
二叉查找树
二叉查找树又被称为二叉搜索树。设 x 为二叉查找树的一个节点,x 节点包含关键字 key,x 的左子树的 key 值都比 x 小,x 的右子树的 key 值都比 x 大。
-
红黑树
红黑树(Red-Black Tree,简称 RB-Tree)是一种平衡的二叉查找树,用途广泛。比如:
TreeMap,TreeSet,HashMap 在 JDK 1.8 后也使用了红黑树。
红黑树的实现比较复杂,但它的操作有着良好的最坏运行时间,并且在实践中是高效的,它可以在 O(logn)时间内做查找,插入和删除操作。
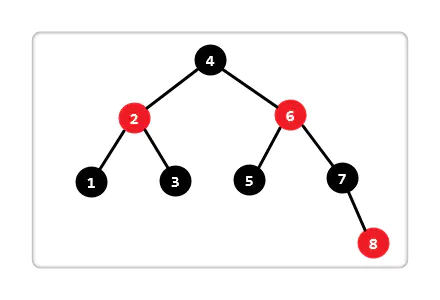
红黑树可以总结为四个性质:
- 每个节点要么是红色的,要么黑色的。
- 根节点是黑色的。
- 如果一个节点是红色的,那么它的两个孩子都是黑色的。
- 对于任意一个节点,其到叶子节点的每条路径上都包含相同数目的黑色节点。
与 AVL(平衡二叉查找树)通过约束左右子树高度不同,红黑树是通过它的四条性质来实现“平衡状态”。在插入节点或者删除节点时,可能会造成某个节点违反了上述某条性质,那么红黑树会通过重新着色和旋转两种方式使之重新复合性质。