类型:给出一些形如$a-b<=k$的不等式(或$a-b>=k$或$a-b<k$或$a-b>k$等),问是否有解或求差的极值。
例子:$b-a<=k1$,$c-b<=k2$,$c-a<=k3$。将$a$,$b$,$c$转换为节点;$k1$,$k2$,$k3$转换为边权;减数指向被减数,形成一个有向图:
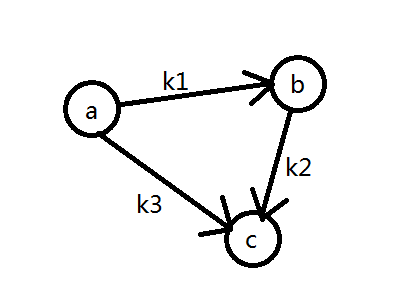
由题可得$(b-a) + (c-b) <= k1+k2$,$c-a<=k1+k2$。比较$k1+k2$与$k3$,其中较小者就是$c-a$的最大值。
由此我们可以得知求差的最大值,即上限被约束,此时我们拿最小的限制,也就是跑最短路;反之,求差的最小值,下限被约束,我们跑最长路。
跑最短路时:$d[v]<=d[u]+w$
跑最长路时:$d[v]>=d[u]+w$
路径中可能会存在负边,我们用SPFA跑。
例题1:UESTC 1961
题解:设sum[x]为前x个咕咕中至少需要赶走的咕咕数,则$sum[b]-sum[a-1]>=c$表示$[a,b]$区间至少赶走c只。题目中选择的是最少,我们需要跑最长路,因存在负边,所以以SPFA进行操作。$d[v]>=d[u]+w$,前面我们可以推出第一个式子$sum[b]>=sum[a-1]+c$,但是如果只连这些边,整张图连通不起来。我们发现$i$和$i+1$存在关系$0<=sum[i+1]-sum[i]<=1$,这个其实就是表示$i+1$那个位置赶与不赶。推出第二个和第三个式子:$sum[i]>=sum[i+1]-1,sum[i+1]>=sum[i]+0$。
由以上式子得到边:$a-1点 b点 距离c$
$i+1点 i点 距离-1$
$i点 i+1点 距离0$

1 #include <queue> 2 #include <cstdio> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 8 const int INF=0x3f3f3f3f; 9 const int N=2e5+10; 10 int k,n,cnt; 11 int st=INF,en=-INF; 12 bool vis[N]; 13 int head[2*N],d[N]; 14 15 struct Edge{ 16 int to,next,w; 17 }edge[N]; 18 19 void add(int u,int v,int w){ 20 edge[cnt].w=w;edge[cnt].to=v;edge[cnt].next=head[u];head[u]=cnt++; 21 } 22 23 void init(){ 24 cnt=0; 25 memset(head,-1,sizeof(head)); 26 } 27 28 void SPFA(){ 29 for(int i=st;i<=en;i++) d[i]=-INF; 30 memset(vis,false,sizeof(vis)); 31 d[st]=0; 32 queue <int> Q; 33 Q.push(st); 34 vis[st]=true; 35 while(!Q.empty()){ 36 int u=Q.front(); 37 Q.pop(); 38 vis[u]=false; 39 for(int i=head[u];~i;i=edge[i].next){ 40 int v=edge[i].to; 41 if(d[v]<d[u]+edge[i].w){ 42 d[v]=d[u]+edge[i].w; 43 if(!vis[v]){ 44 Q.push(v); 45 vis[v]=true; 46 } 47 } 48 } 49 } 50 } 51 52 int main(){ 53 init(); 54 scanf("%d%d",&k,&n); 55 for(int i=1;i<=n;i++){ 56 int a,b,c; 57 scanf("%d%d%d",&a,&b,&c); 58 add(a-1,b,c); 59 st=min(st,a-1); 60 en=max(en,b); 61 } 62 for(int i=st;i<en;i++){ 63 add(i,i+1,0); 64 add(i+1,i,-1); 65 } 66 SPFA(); 67 printf("%d ",d[en]); 68 return 0; 69 }
例题2:POJ 1364
题解:最短路式子:$d[v]<=d[u]+w$
式子1:$sum[a+b+1]-sum[a]>c$ —> $sum[a]<=sum[a+b+1]-c-1$ —> $a+b+1quad aquad -c-1$
式子2:$sum[a+b+1]-sum[a]<c$ —> $sum[a+b+1]<=sum[a]+c-1$ —> $aquad a+b+1quad c-1$
注意:先移项,移项完后再处理没有等于的情况。

1 #include <queue> 2 #include <cstdio> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 8 const int N=1234; 9 const int INF=0x3f3f3f3f; 10 int n,m,cnt; 11 int head[2*N],d[N],Time[N]; 12 bool vis[N]; 13 14 struct Edge{ 15 int to,next,w; 16 }edge[N]; 17 18 void add(int u,int v,int w){ 19 edge[cnt].w=w;edge[cnt].to=v;edge[cnt].next=head[u];head[u]=cnt++; 20 } 21 22 void init(){ 23 cnt=0; 24 memset(Time,0,sizeof(Time)); 25 memset(head,-1,sizeof(head)); 26 } 27 28 bool SPFA(int st){ 29 for(int i=0;i<N;i++) d[i]=INF; 30 memset(vis,false,sizeof(vis)); 31 queue <int> Q; 32 Q.push(st); 33 d[st]=0; 34 vis[st]=true; 35 Time[st]=1; 36 while(!Q.empty()){ 37 int u=Q.front(); 38 Q.pop(); 39 vis[u]=false; 40 for(int i=head[u];~i;i=edge[i].next){ 41 int v=edge[i].to; 42 if(d[v]>d[u]+edge[i].w){ 43 d[v]=d[u]+edge[i].w; 44 if(!vis[v]){ 45 Q.push(v); 46 vis[v]=true; 47 Time[v]++; 48 if(Time[v]>n) return false; 49 } 50 } 51 } 52 } 53 return true; 54 } 55 56 int main(){ 57 while(scanf("%d",&n)!=EOF&&n){ 58 init(); 59 scanf("%d",&m); 60 char op[10]; 61 for(int i=1;i<=n;i++) add(0,i,0); 62 for(int i=1;i<=m;i++){ 63 int a,b,c; 64 scanf("%d%d%s%d",&a,&b,&op,&c); 65 if(op[0]=='g') add(a+b+1,a,-c-1); 66 else add(a,a+b+1,c-1); 67 } 68 if(SPFA(0)) printf("lamentable kingdom "); 69 else printf("successful conspiracy "); 70 } 71 return 0; 72 }
例题3:HDU 3666
题解:由题意得:$L<=c[i][j]*a[i]/b[j]<=U$ 两边除以$c[i][j]$ —> $L/c[i][j] <= a[i]/b[j] <= U/c[i][j]$,先两边取对数,得到$log(L/c[i][j])quad <=quad log(a[i])-log(b[j])quad <=quad log(U/c[i][j])$,推导出两个式子:
式子1:$log(a[i])<=log(U/c[i][j])+log(b[j])$
式子2:$log(b[j])<=log(a[i])-log(L/c[i][j])$
注意:log取double型,$n$个$a$和$m$个$b$连接,保证了图的连通性,不需要新建边。数据范围注意,有$n*m$个点和$2*n*m$条边。还有注意剪枝。

1 #include <queue> 2 #include <cstdio> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 8 const int M=1e6+10; 9 const int N=400+10; 10 const double INF=1e12; 11 int n,m,cnt,head[M]; 12 double l,r,c[N][N],d[N]; 13 bool vis[N]; 14 15 struct Edge{ 16 int to,next; 17 double w; 18 }edge[M]; 19 20 void add(int u,int v,double w){ 21 edge[cnt].w=w;edge[cnt].to=v;edge[cnt].next=head[u];head[u]=cnt++; 22 } 23 24 void init(){ 25 cnt=0; 26 memset(head,-1,sizeof(head)); 27 } 28 29 bool SPFA(int st){ 30 int CNT=0; 31 for(int i=0;i<N;i++) d[i]=INF; 32 memset(vis,false,sizeof(vis)); 33 queue <int> Q; 34 Q.push(st); 35 d[st]=0; 36 vis[st]=true; 37 while(!Q.empty()){ 38 CNT++; 39 if(CNT>2*(n+m)) return false; 40 int u=Q.front(); 41 Q.pop(); 42 vis[u]=false; 43 for(int i=head[u];~i;i=edge[i].next){ 44 int v=edge[i].to; 45 if(d[v]>d[u]+edge[i].w){ 46 d[v]=d[u]+edge[i].w; 47 if(!vis[v]){ 48 Q.push(v); 49 vis[v]=true; 50 } 51 } 52 } 53 } 54 return true; 55 } 56 57 int main(){ 58 59 while(scanf("%d%d%lf%lf",&n,&m,&l,&r)!=EOF){ 60 init(); 61 l=log(l);r=log(r); 62 for(int i=1;i<=n;i++){ 63 for(int j=1;j<=m;j++){ 64 scanf("%lf",&c[i][j]); 65 add(i,j+n,log(1.0*c[i][j])-l); 66 add(j+n,i,r-log(1.0*c[i][j])); 67 } 68 } 69 if(SPFA(1)) printf("YES "); 70 else printf("NO "); 71 } 72 73 return 0; 74 }
例题4:HDU 1384
与第一题相同

1 #include <queue> 2 #include <cstdio> 3 #include <cstring> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 8 const int INF=0x3f3f3f3f; 9 const int N=2e5+10; 10 int k,n,cnt; 11 int st=INF,en=-INF; 12 bool vis[N]; 13 int head[2*N],d[N]; 14 15 struct Edge{ 16 int to,next,w; 17 }edge[N]; 18 19 void add(int u,int v,int w){ 20 edge[cnt].w=w;edge[cnt].to=v;edge[cnt].next=head[u];head[u]=cnt++; 21 } 22 23 void init(){ 24 cnt=0; 25 memset(head,-1,sizeof(head)); 26 } 27 28 void SPFA(){ 29 for(int i=st;i<=en;i++) d[i]=-INF; 30 memset(vis,false,sizeof(vis)); 31 d[st]=0; 32 queue <int> Q; 33 Q.push(st); 34 vis[st]=true; 35 while(!Q.empty()){ 36 int u=Q.front(); 37 Q.pop(); 38 vis[u]=false; 39 for(int i=head[u];~i;i=edge[i].next){ 40 int v=edge[i].to; 41 if(d[v]<d[u]+edge[i].w){ 42 d[v]=d[u]+edge[i].w; 43 if(!vis[v]){ 44 Q.push(v); 45 vis[v]=true; 46 } 47 } 48 } 49 } 50 } 51 52 int main(){ 53 while(scanf("%d",&n)!=EOF){ 54 init(); 55 for(int i=1;i<=n;i++){ 56 int a,b,c; 57 scanf("%d%d%d",&a,&b,&c); 58 add(a-1,b,c); 59 st=min(st,a-1); 60 en=max(en,b); 61 } 62 for(int i=st;i<en;i++){ 63 add(i,i+1,0); 64 add(i+1,i,-1); 65 } 66 SPFA(); 67 printf("%d ",d[en]); 68 } 69 return 0; 70 }
