PCB 板边倒圆角的实现方法（基本算法一）

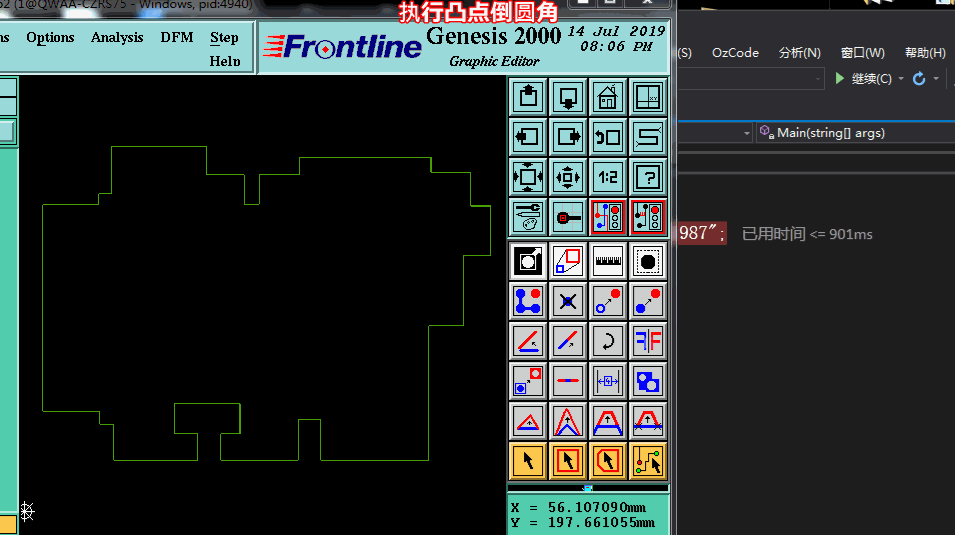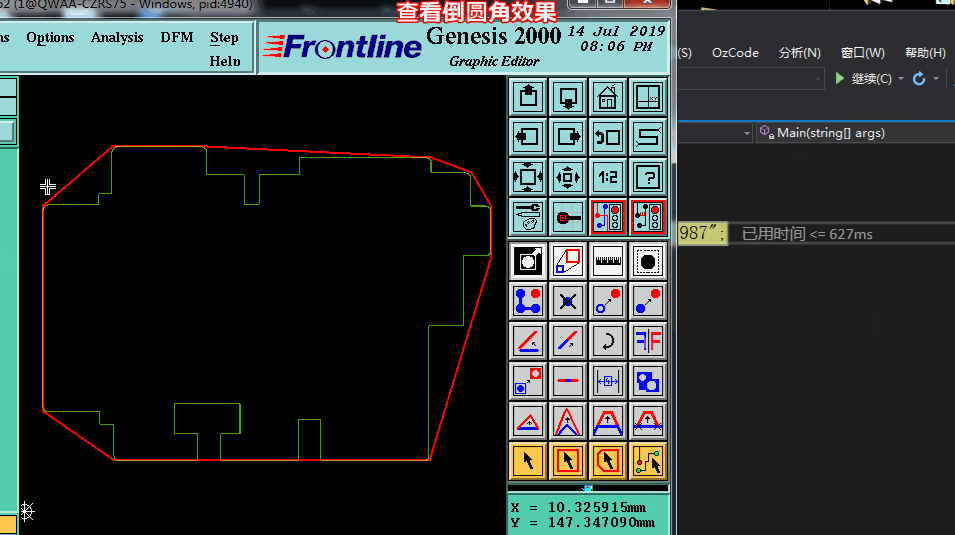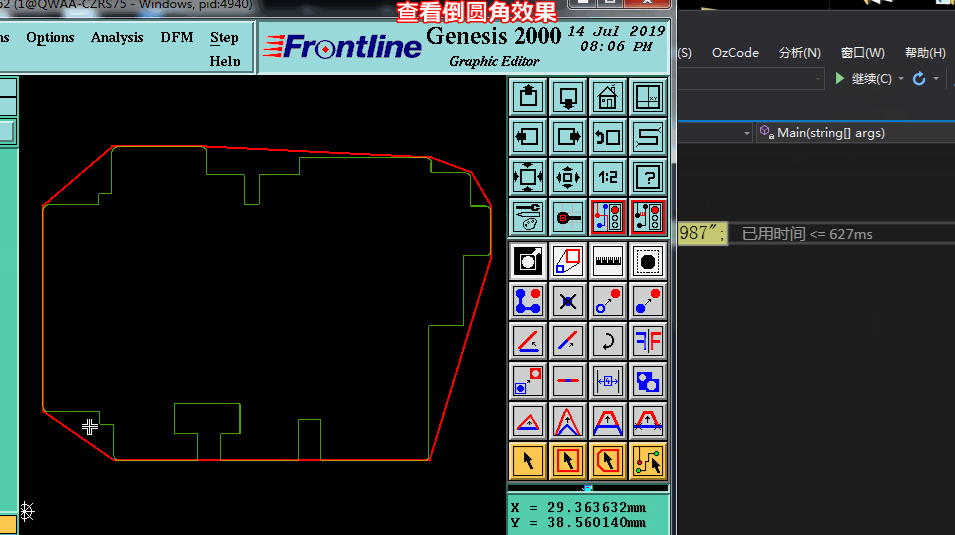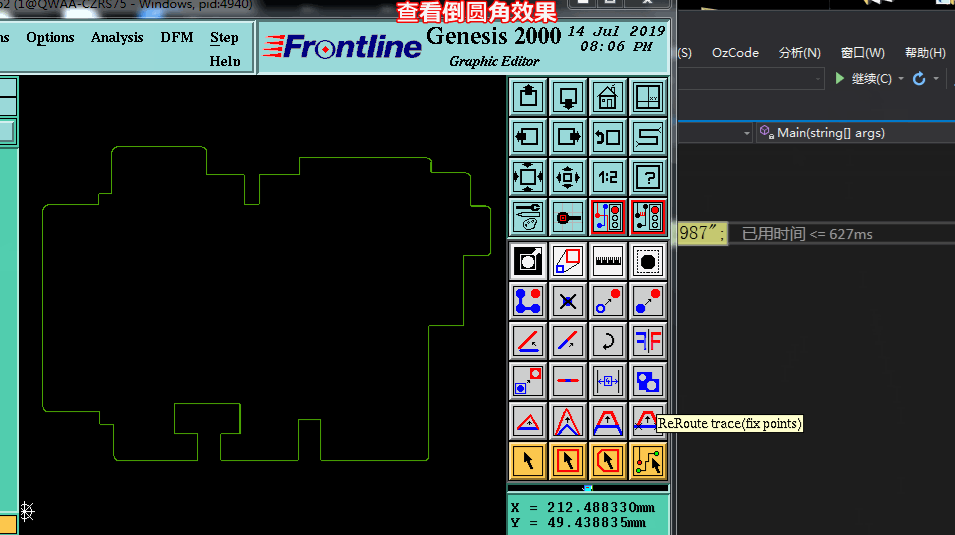
当PCB外形是直角时,通常工程制作外形(锣带）时,会将直角或尖角的地方倒成圆角，主要是为了防止PCB容易划伤板他扎伤人

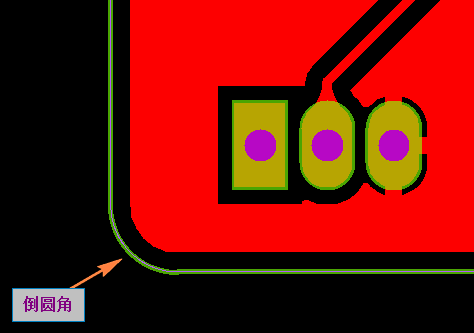
所以当客户没有特殊要求时,PCB外形是直角一般会默认倒角0.5mm圆角(如下图所示)

 一.PCB板边倒圆角点分析

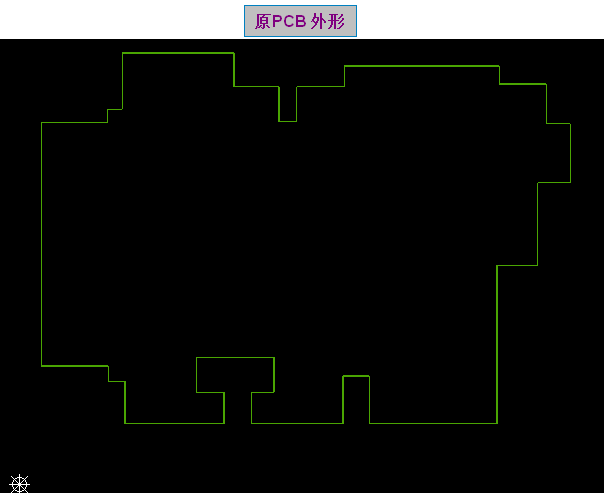
   原PCB外形  如下图图示:看了这个PCB外形,产生有2个问题点.

    1.外形中哪些点需倒圆角?

    2.如何怎么倒圆角?

 

 1.外形中哪些点需倒圆角?

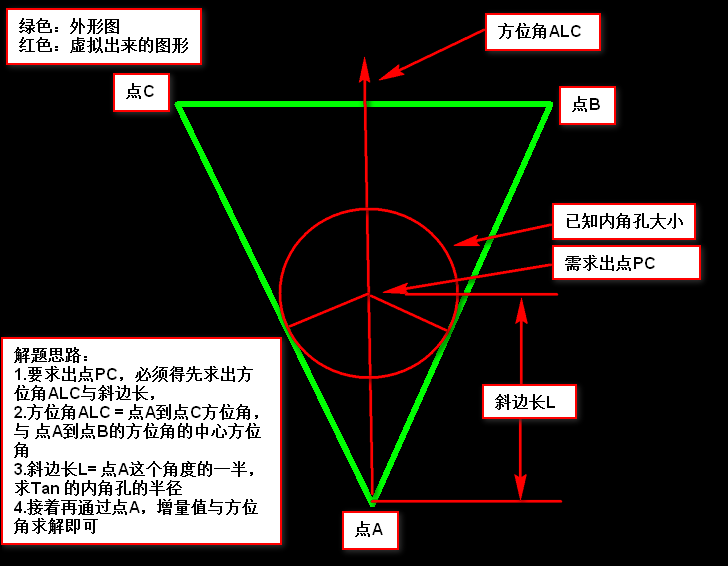
看下图: PCB外形倒圆角的点,刚好就是我们凸包需求出的点,接下来我们将玩转凸包了,只要求出凸包，那么就可以实现PCB板边倒圆角啦。

 

   求凸包的算法：我们可以借鉴算法导论中的查找凸包的算法（加以改进得到新的求凸包方法，详见【方法一】与【方法二】）

 

 2.如何怎么倒圆角?

  在下面有说明倒角方法.

 二. 求凸点

    方法一求凸点:【采用多轮遍历,一遍一遍将凹点踢除，剩于的即是凸点】

 

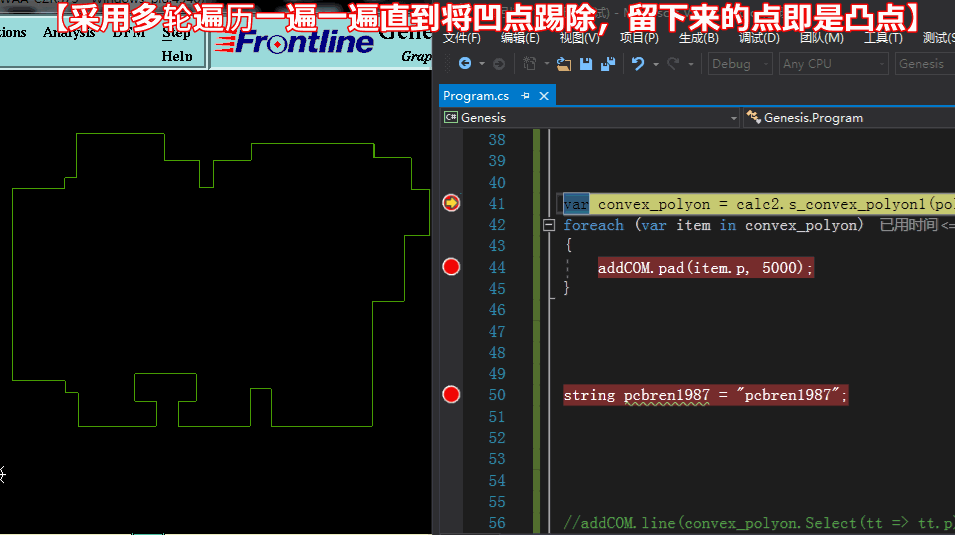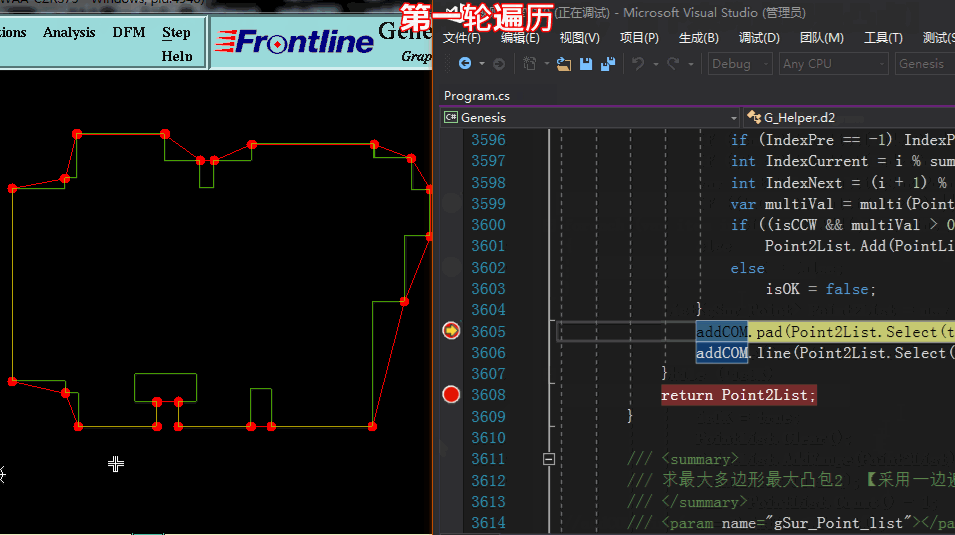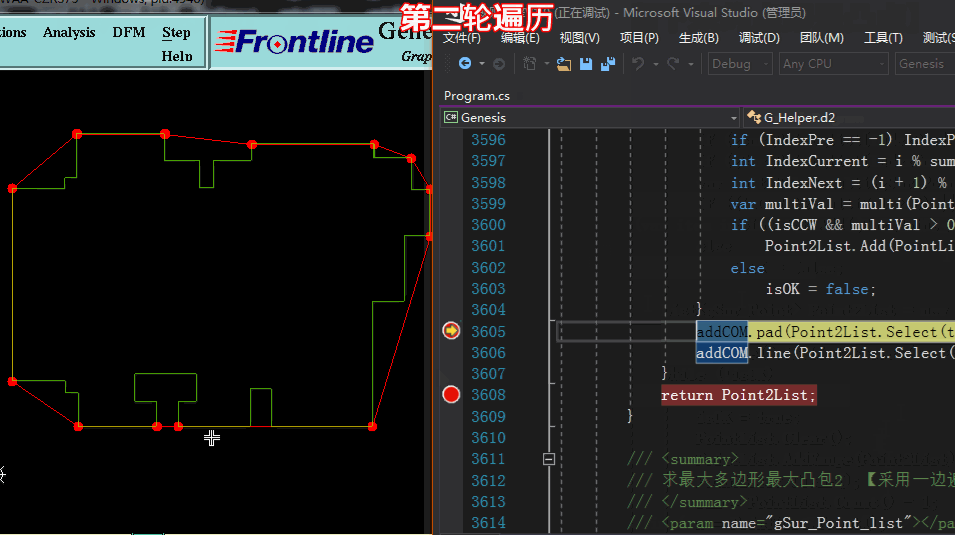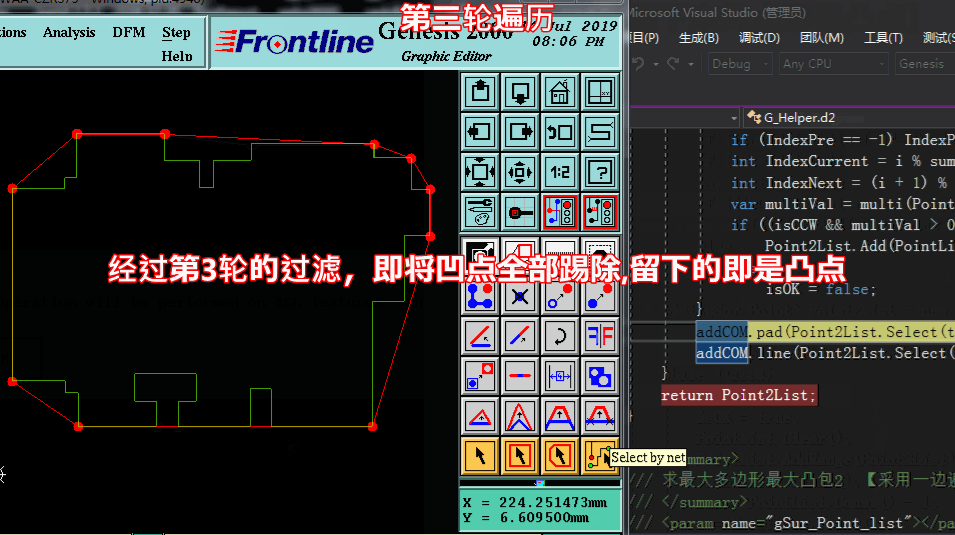
    方法一求凸点:  代码

        /// <summary>
        /// 求最大多边形最大凸包1  【采用多轮遍历将凹点踢除，剩于的即是凸点】
        /// </summary>
        /// <param name="gSur_Point_list"></param>
        /// <returns></returns>
        public List<gSur_Point> s_convex_polyon1(List<gSur_Point> gSur_Point_list)
        {
            add addCOM = new add();
            bool isOK = true;
            List<gSur_Point> PointList = new List<gSur_Point>();
            var isCCW = s_isCCW(gSur_Point_list);
            int sum = gSur_Point_list.Count() - 1;
            int n = gSur_Point_list.Count();
            for (int i = 0; i < n; i++)
            {
                int IndexPre = (i - 1) % sum;
                if (IndexPre == -1) IndexPre = sum - 1;
                int IndexCurrent = i % sum;
                int IndexNext = (i + 1) % sum;
                if (gSur_Point_list[IndexPre].type_point > 0) continue;
                if (gSur_Point_list[IndexCurrent].type_point > 0) continue;
                var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
                if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                    PointList.Add(gSur_Point_list[IndexCurrent]);
                else
                    isOK = false;
            }
            List<gSur_Point> Point2List = new List<gSur_Point>(PointList);
            while (!isOK)
            {
                isOK = true;
                PointList.Clear();
                PointList.AddRange(Point2List);
                Point2List.Clear();
                sum = PointList.Count() - 1;
                n = PointList.Count();
                for (int i = 0; i < n; i++)
                {
                    int IndexPre = (i - 1) % sum;
                    if (IndexPre == -1) IndexPre = sum - 1;
                    int IndexCurrent = i % sum;
                    int IndexNext = (i + 1) % sum;
                    var multiVal = multi(PointList[IndexPre].p, PointList[IndexCurrent].p, PointList[IndexNext].p);
                    if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                        Point2List.Add(PointList[IndexCurrent]);
                    else
                        isOK = false;
                }
            }
            return Point2List;
        }

方法二求凸包：【采用一边遍历找出凸点并加入队列，并同时将队列中的凸点队列中找出凹点踢除】

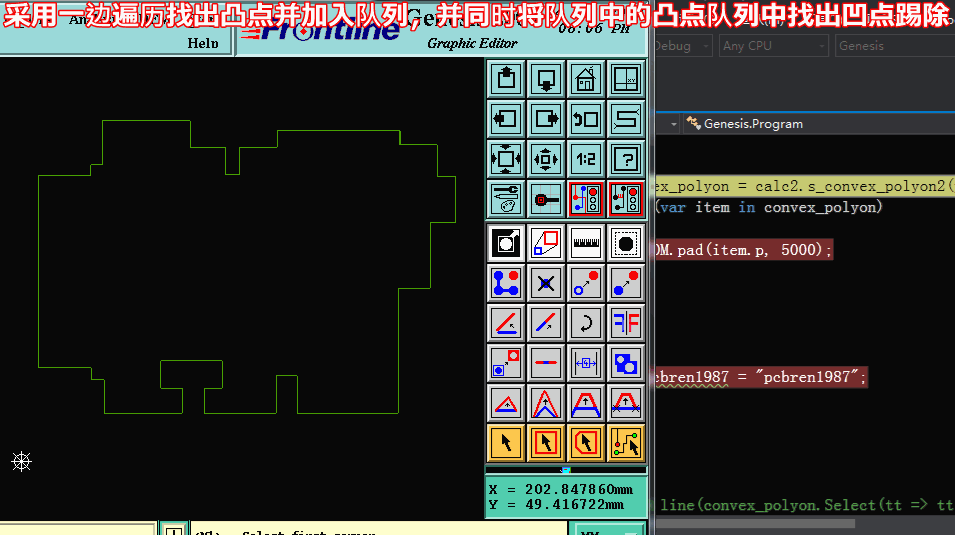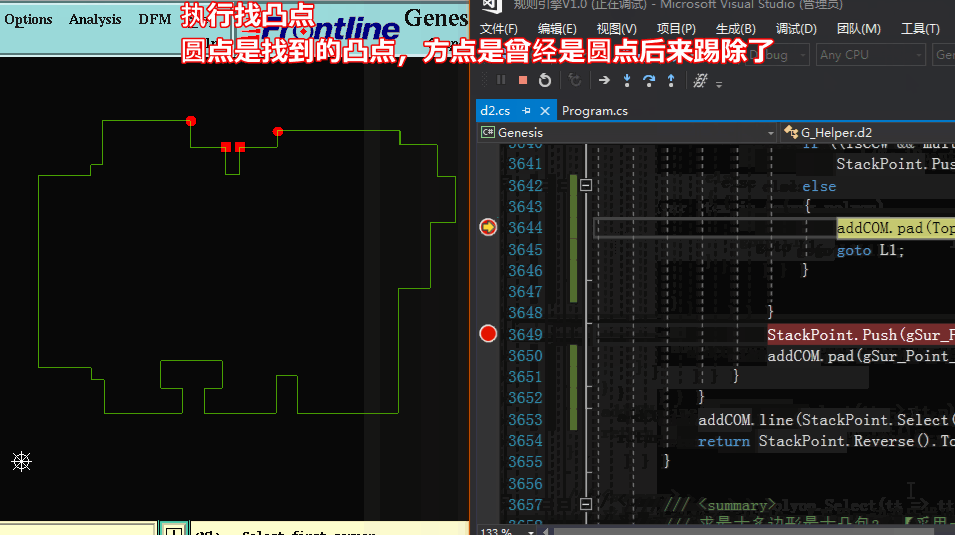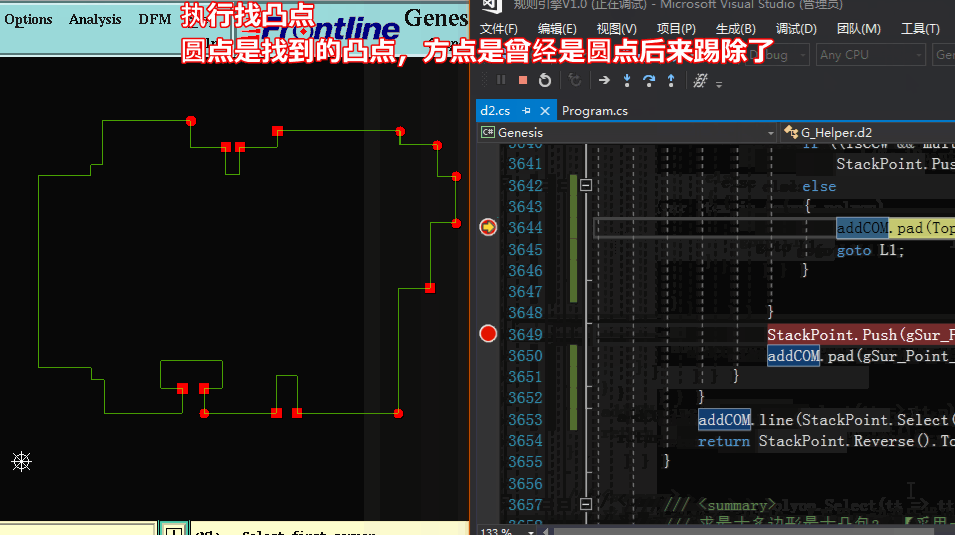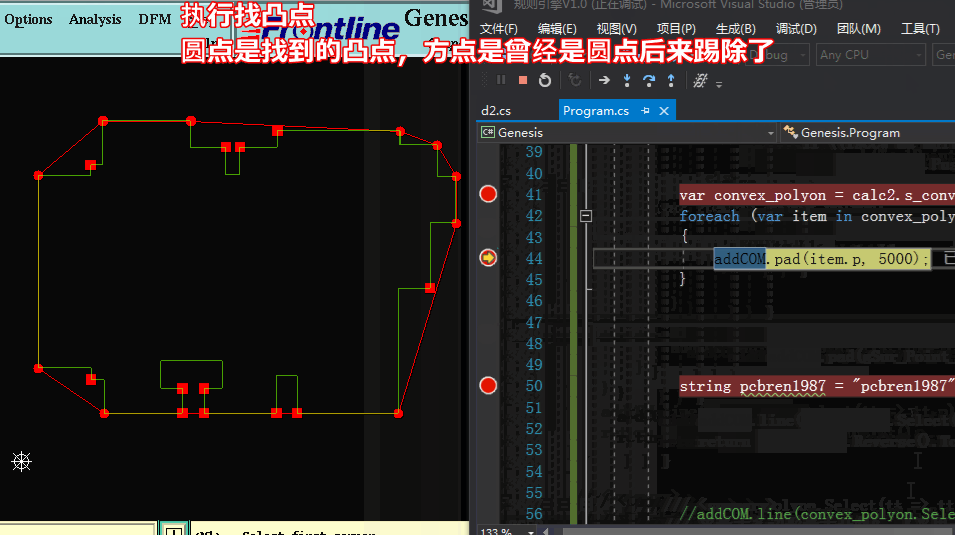
 方法二求凸包代码:

        /// <summary>
        /// 求最大多边形最大凸包2  【采用一边遍历找出凸点并加入队列，并同时将队列中的凸点队列中找出凹点踢除】
        /// </summary>
        /// <param name="gSur_Point_list"></param>
        /// <returns></returns>
        public List<gSur_Point> s_convex_polyon2(List<gSur_Point> gSur_Point_list)
        {
            Stack<gSur_Point> StackPoint = new Stack<gSur_Point>();
            var isCCW = s_isCCW(gSur_Point_list);
            int sum = gSur_Point_list.Count() - 1;
            int n = gSur_Point_list.Count();
            for (int i = 0; i < n; i++)
            {
                int IndexPre = (i - 1) % sum;
                if (IndexPre == -1) IndexPre = sum - 1;
                int IndexCurrent = i % sum;
                int IndexNext = (i + 1) % sum;
                if (gSur_Point_list[IndexPre].type_point > 0) continue;
                if (gSur_Point_list[IndexCurrent].type_point > 0) continue;
                var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
                if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                {
                    L1:
                    if (StackPoint.Count > 1)
                    {
                        var Top1Point = StackPoint.Pop();
                        var Top2Point = StackPoint.Peek();
                        multiVal = multi(Top2Point.p, Top1Point.p, gSur_Point_list[IndexCurrent].p);
                        if ((isCCW && multiVal > 0) || (!isCCW && multiVal < 0))
                            StackPoint.Push(Top1Point);
                        else
                            goto L1;   
                    }
                    StackPoint.Push(gSur_Point_list[IndexCurrent]);
                }
            }
            return StackPoint.Reverse().ToList();
        }

方法三求凸包:【按算法导论Graham扫描法 各节点按方位角+距离 逆时针排序  依次检查,当不属凸点于则弹出】

 

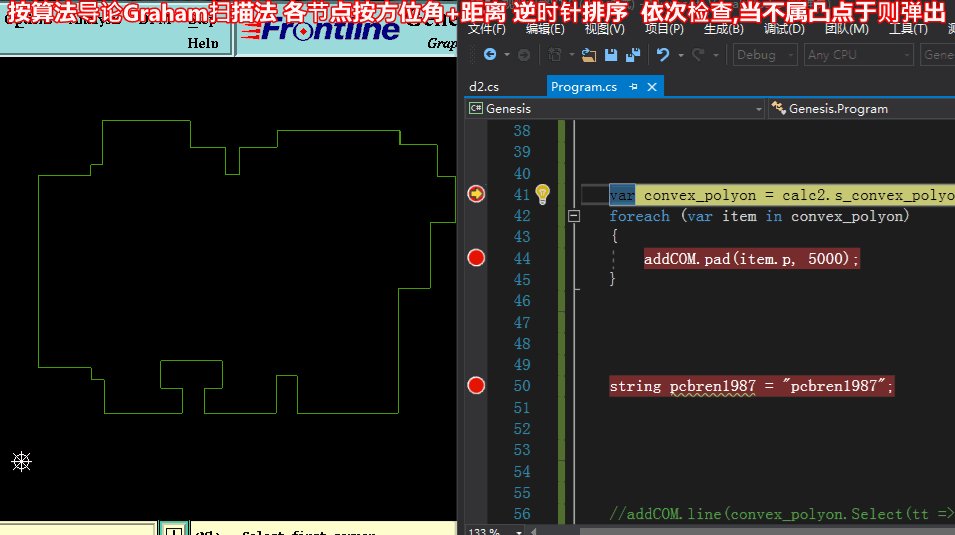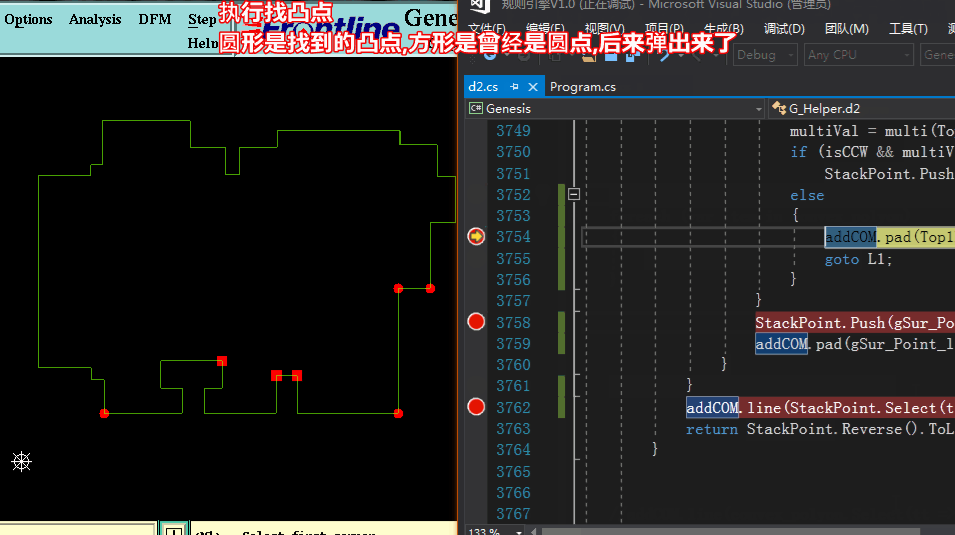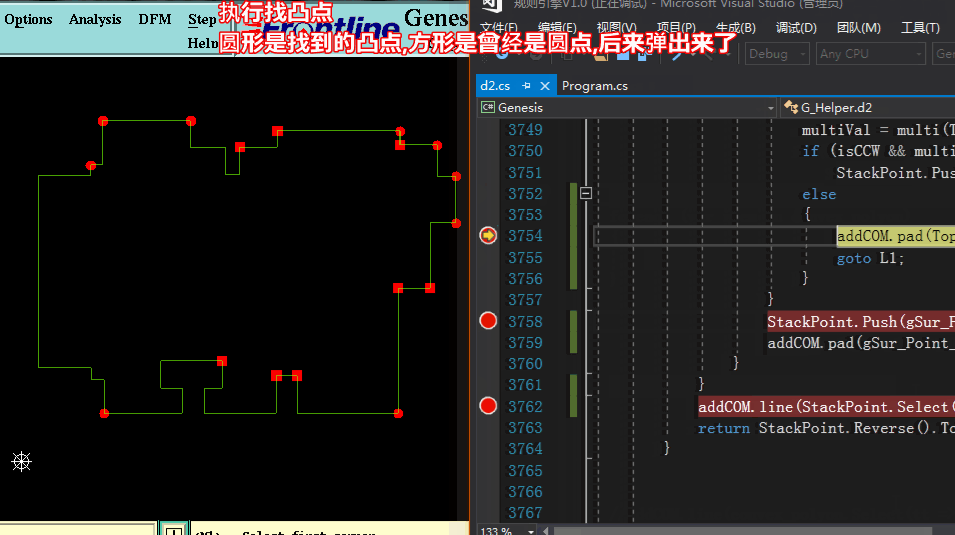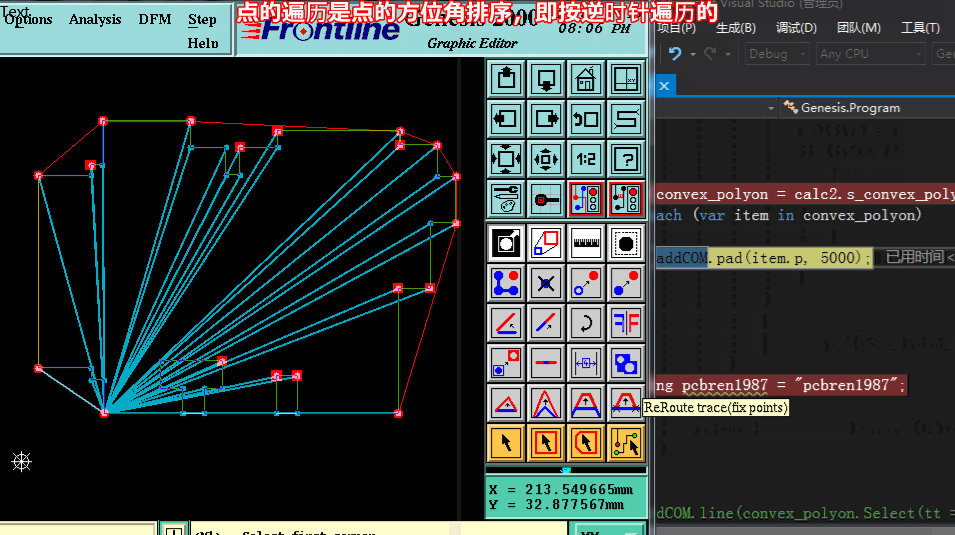
 方法三求凸包代码

        /// <summary>
        /// 求最大多边形最大凸包5  【按算法导论Graham扫描法 各节点按方位角+距离 逆时针排序  依次检查,当不属凸点于则弹出】
        /// 由于把各点的排列顺序重新排序了，只支持折线节点(当存在弧节点时会出异常 ！！！)
        /// </summary>
        /// <param name="gSur_Point_list"></param>
        /// <returns></returns>
        public List<gSur_Point> s_convex_polyon3(List<gSur_Point> gSur_Point_list)
        {
            var LeftBottomPoint = gSur_Point_list.OrderBy(tt => tt.p.y).ThenBy(tt => tt.p.x).FirstOrDefault();
            gSur_Point_list.RemoveAt(gSur_Point_list.Count - 1);
            gSur_Point_list.ForEach(tt =>
                                        {
                                            tt.Value = p2p_di(LeftBottomPoint.p, tt.p);
                                            tt.Angle = p_ang(LeftBottomPoint.p, tt.p);
                                        }
                );
            gSur_Point_list = gSur_Point_list.OrderBy(tt => tt.Angle).ThenBy(tt => tt.Value).ToList();
            gSur_Point_list.Add(gSur_Point_list[0]);
            Stack<gSur_Point> StackPoint = new Stack<gSur_Point>();
            var isCCW = true;
            int sum = gSur_Point_list.Count() - 1;
            int n = gSur_Point_list.Count();
            for (int i = 0; i < n; i++)
            {
                int IndexPre = (i - 1) % sum;
                if (IndexPre == -1) IndexPre = sum - 1;
                int IndexCurrent = i % sum;
                int IndexNext = (i + 1) % sum;
                var multiVal = multi(gSur_Point_list[IndexPre].p, gSur_Point_list[IndexCurrent].p, gSur_Point_list[IndexNext].p);
                if (isCCW && multiVal > 0)
                {
                    L1:
                    if (StackPoint.Count > 1)
                    {
                        var Top1Point = StackPoint.Pop();
                        var Top2Point = StackPoint.Peek();
                        multiVal = multi(Top2Point.p, Top1Point.p, gSur_Point_list[IndexCurrent].p);
                        if (isCCW && multiVal > 0)
                            StackPoint.Push(Top1Point);
                        else
                            goto L1;
                    }
                    StackPoint.Push(gSur_Point_list[IndexCurrent]);
                }
            }
            return StackPoint.Reverse().ToList();
        }

             

公共方法与数据结构

    /// <summary>
    /// Surface 坐标泛型集类1
    /// </summary>
    public class gSur_Point
    {
        public gSur_Point()
        { }
        public gSur_Point(double x_val, double y_val, byte type_point_)
        {
            this.p.x = x_val;
            this.p.y = y_val;
            this.type_point = type_point_;
        }
        public gSur_Point(gPoint p, byte type_point_)
        {
            this.p = p;
            this.type_point = type_point_;
        }
        public gPoint p;
        /// <summary>
        /// 0为折点  1为顺时针 2为逆时针  
        /// </summary>
        public byte type_point { get; set; } = 0;
        /// <summary>
        /// 值
        /// </summary>
        public double Value { get; set; } = 0;
        /// <summary>
        /// 角度
        /// </summary>
        public double Angle { get; set; } = 0;
        /// <summary>
        /// 标记
        /// </summary>
        public bool isFalg { get; set; } 
    }
    /// <summary>
    /// 点  数据类型 (XY)
    /// </summary>
    public struct gPoint
    {
        public gPoint(gPoint p_)
        {
            this.x = p_.x;
            this.y = p_.y;
        }
        public gPoint(double x_val, double y_val)
        {
            this.x = x_val;
            this.y = y_val;
        }
        public double x;
        public double y;
        public static gPoint operator +(gPoint p1, gPoint p2)
        {
            p1.x += p2.x;
            p1.y += p2.y;
            return p1;
        }
        public static gPoint operator -(gPoint p1, gPoint p2)
        {
            p1.x -= p2.x;
            p1.y -= p2.y;
            return p1;
        }
        public static gPoint operator +(gPoint p1, double val)
        {
            p1.x += val;
            p1.y += val;
            return p1;
        }
        public static bool operator ==(gPoint p1, gPoint p2)
        {
            return (p1.x == p2.x && p1.y == p2.y);
        }
        public static bool operator !=(gPoint p1, gPoint p2)
        {
            return !(p1.x == p2.x && p1.y == p2.y);
        }
    }
        /// <summary>
        /// 求叉积   判断【点P与线L】位置关系【小于0】在右边   【大于0】在左边   【等于0】共线
        /// </summary>
        /// <param name="ps"></param>
        /// <param name="pe"></param>
        /// <param name="p"></param>
        /// <returns>【小于0】在右边   【大于0】在左边   【等于0】共线</returns>
        public double multi(gPoint ps, gPoint pe, gPoint p)
        {
            return ((ps.x - p.x) * (pe.y - p.y) - (pe.x - p.x) * (ps.y - p.y));
        }
        /// <summary>
        /// 检测 Surface是否逆时针   
        /// </summary>
        /// <param name="gSur_Point_list"></param>
        /// <returns></returns>
        public bool s_isCCW(List<gSur_Point> gSur_Point_list)
        {
            double d = 0;
            int n = gSur_Point_list.Count() - 1;
            for (int i = 0; i < n; i++)
            {
                if (gSur_Point_list[i].type_point > 0) continue;
                int NextI = i + 1 + (gSur_Point_list[i + 1].type_point > 0 ? 1 : 0);
                d += -0.5 * (gSur_Point_list[NextI].p.y + gSur_Point_list[i].p.y) * (gSur_Point_list[NextI].p.x - gSur_Point_list[i].p.x);
            }
            return d > 0;
        }
        /// <summary>
        /// 返回两点之间欧氏距离
        /// </summary>
        /// <param name="p1"></param>
        /// <param name="p2"></param>
        /// <returns></returns>
        public double p2p_di(gPoint p1, gPoint p2)
        {
            return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
        }
        /// <summary>
        /// 求方位角
        /// </summary>
        /// <param name="ps"></param>
        /// <param name="pe"></param>
        /// <returns></returns>
        public double p_ang(gPoint ps, gPoint pe)
        {
            double a_ang = Math.Atan((pe.y - ps.y) / (pe.x - ps.x)) / Math.PI * 180;
            //象限角  转方位角   计算所属象限   并求得方位角
            if (pe.x >= ps.x && pe.y >= ps.y)  //↗    第一象限
            {
                return a_ang;
            }
            else if (!(pe.x >= ps.x) && pe.y >= ps.y)  // ↖   第二象限
            {
                return a_ang + 180;
            }
            else if (!(pe.x >= ps.x) && !(pe.y >= ps.y))  //↙   第三象限
            {
                return a_ang + 180;
            }
            else if (pe.x >= ps.x && !(pe.y >= ps.y))  // ↘   第四象限
            {
                return a_ang + 360;
            }
            else
            {
                return a_ang;
            }
        }

 三.板边凸点倒圆角方法

     方法一.也最简单的倒角方法,我们将PCB板边凸点找出来后，可以直接借助genesis倒角功能就可以实现了

                   当然但偶尔会报错的, 且当N个小线段组成的尖角倒角会出错(要实现完美效果只有自己写倒角算法啦)             

             

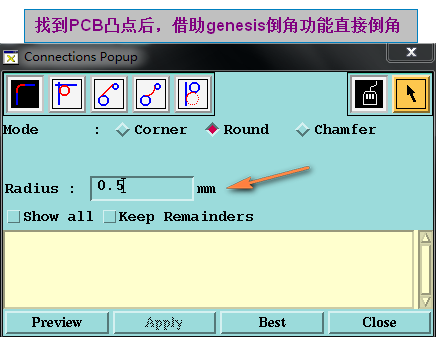
   方法二:自己写倒角算法，这个算法和加内角孔算法类似（这里只是介绍简单的倒角)考虑特殊的需要扩展

         可以参考这篇文章: https://www.cnblogs.com/pcbren/p/9665304.html

            

 四.凸点加倒圆角实现效果