有关直线对称的套路与一些题目

利用直线对称解决问题的最经典例子便是卡特兰数，这里不再多说。顺便安利一位大佬的博客：
https://www.cnblogs.com/LinZhengyu/p/13445696.html
https://www.cnblogs.com/LinZhengyu/p/13451462.html

[JLOI2015]骗我呢

简要题意

给定 (n,m)，求有多少个 (n imes m) 的矩阵，满足：
对于任意的 (i,j)，都满足矩阵中的第 (i) 行第 (j) 列的元素 (x_{i,j}) 有：

1. (x_{i,j}<x_{i,j+1}(j<m))；
2. (x_{i,j}<x_{i-1,j-1}(i,j>1))；
3. (0le x_{i,j}le m)。

结果对 (10^9+7) 取模，(1le n,mle 10^6)。

题解

第 (1) 条性质表示这个矩阵中每行都是单调递增的，而第 (3) 条性质则限制了每个只有 (m+1) 种取值。

我们发现，一行只有 (m) 个元素，而每个元素只可能有 (m+1) 中取值，且行内单调递增。于是这行有且只有一个在 ([0,m]) 中的元素没有被取到，而剩下的元素从小到大排序来填充这一行。

于是我们设计 DP 状态 (f_{i,j}) 表示进行到第 (i) 行，满足第 (i) 行缺少的元素时 (j) 的方案数。

考虑转移，发现如果 (k>j+1) 则对于 (f_{i,p}=j+1)，就会有 (f_{i,p}=j+1=f_{i-1,p+1})，不满足第 (2) 条性质。于是要有 (kle j+1)，所以有转移：(f_{i,j}=sum_{k=1}^{j+1}{f_{i-1,k}})。

再优化一下：(f_{i,j}=sum_{k=0}^{j+1}{f_{i-1,k}}=sum_{k=0}^{j}{f_{i-1,k}}+f_{i-1,j+1}=f_{i,j-1}+f_{i-1,j+1})。

答案就是 (f_{n+1,m})，这样子做是 (O(nm)) 的，要考虑优化。

---

我们考虑这个式子的组合意义，我们先将它映射到坐标轴上。下图中箭头表示转移，而答案就是从 ((1,1)) 走到 ((n,m)) 的路径数量。

这里面有些转移时“斜”的，这不太直观。我们将这个网格图变换一下，将第 (i) 行的点向右平移 (i-1) 格。同时将第 (1) 列之间的转移变成先往上再往右走。得到下图：

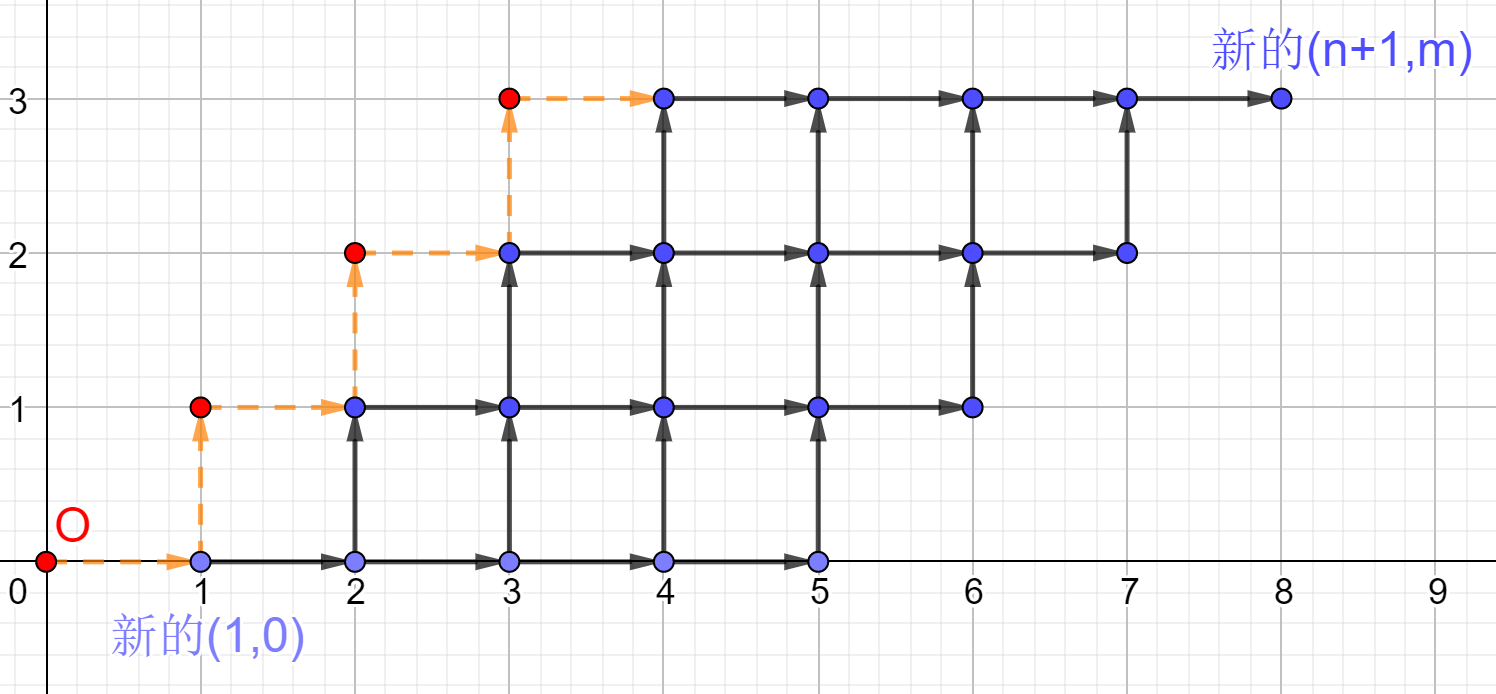
把起点弄到原点上，再画出两条直线：

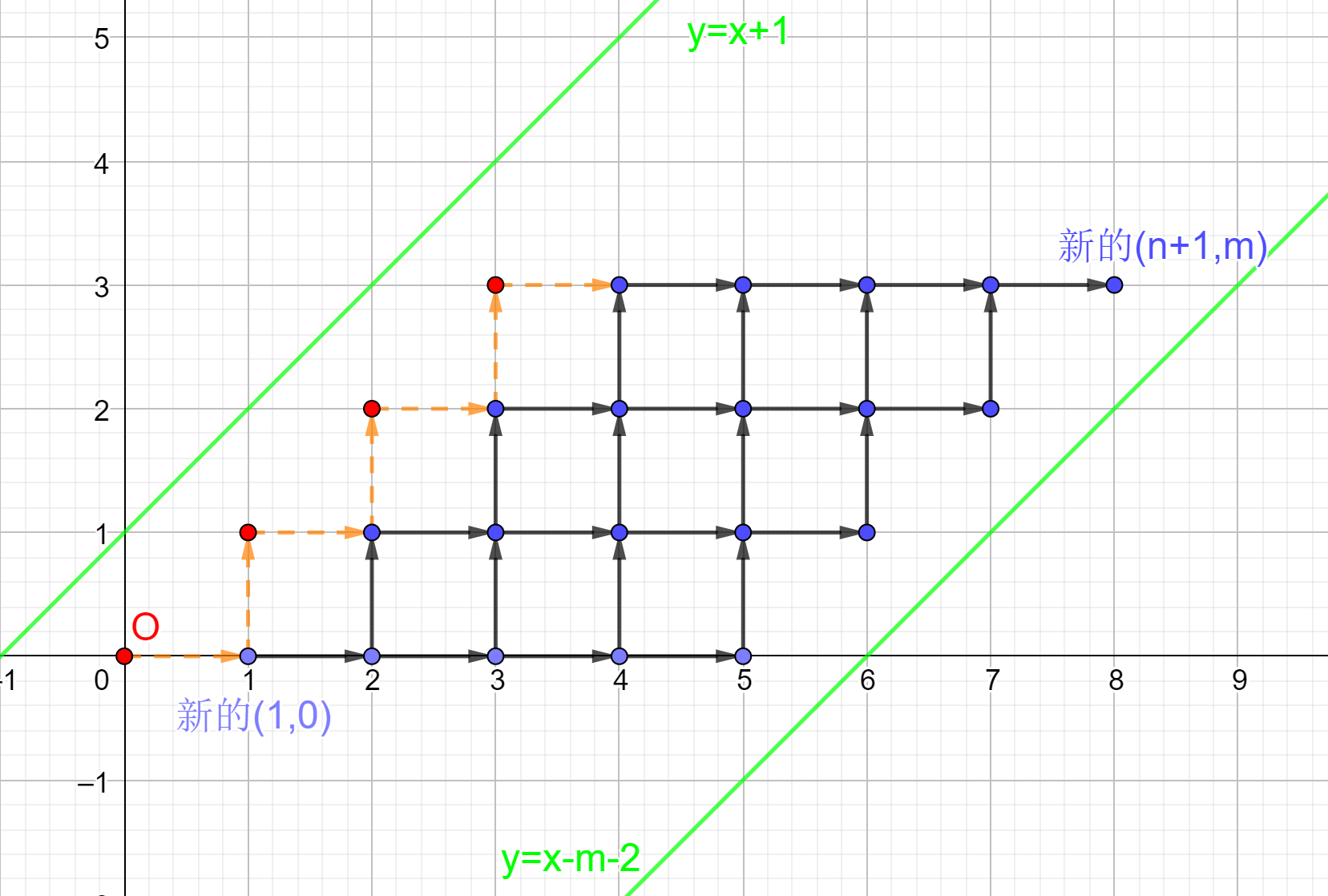
我们发现答案就是从 ((0,0)) 到 (T) 即坐标轴上的 ((n+m+1,n)) 的路径数量，即只能向右或者向上走，不能触碰到 (a:y=x+1) 与 (b:y=x-m-2) 两条直线的从 ((0,0)) 到 ((n+m+1,n)) 的路径数量。

---

如果没有两条直线的限制，那么答案显然就是 (dbinom {x_T+y_T}{x_T})。对于碰到了直线的，例如我们先后触碰到了 (aabbabb)，发现其实连续触碰到相同的直线之没有上面影响的，可以整个缩起来，于是上面的例子可以被缩为 (abab)。

我们回想一下初中奥数“将军饮马”问题，我们发现将 ((n+m+1,n)) 关于 (a) 对称，得到 (A')，则从 ((0,0)) 到 (A') 的每一条路径都和对应的先触碰到 (a) 再折回到 ((n+m+1,n)) 的路径都是一一对应的，数量自然而然也是相等的。这个方法是可以叠加的，例如我们先将 ((n+m+1,n)) 关于 (a) 对称，再关于 (b) 对称，则到对应点的路径数则是结尾为 (ba) 的路径数。可以见下图：

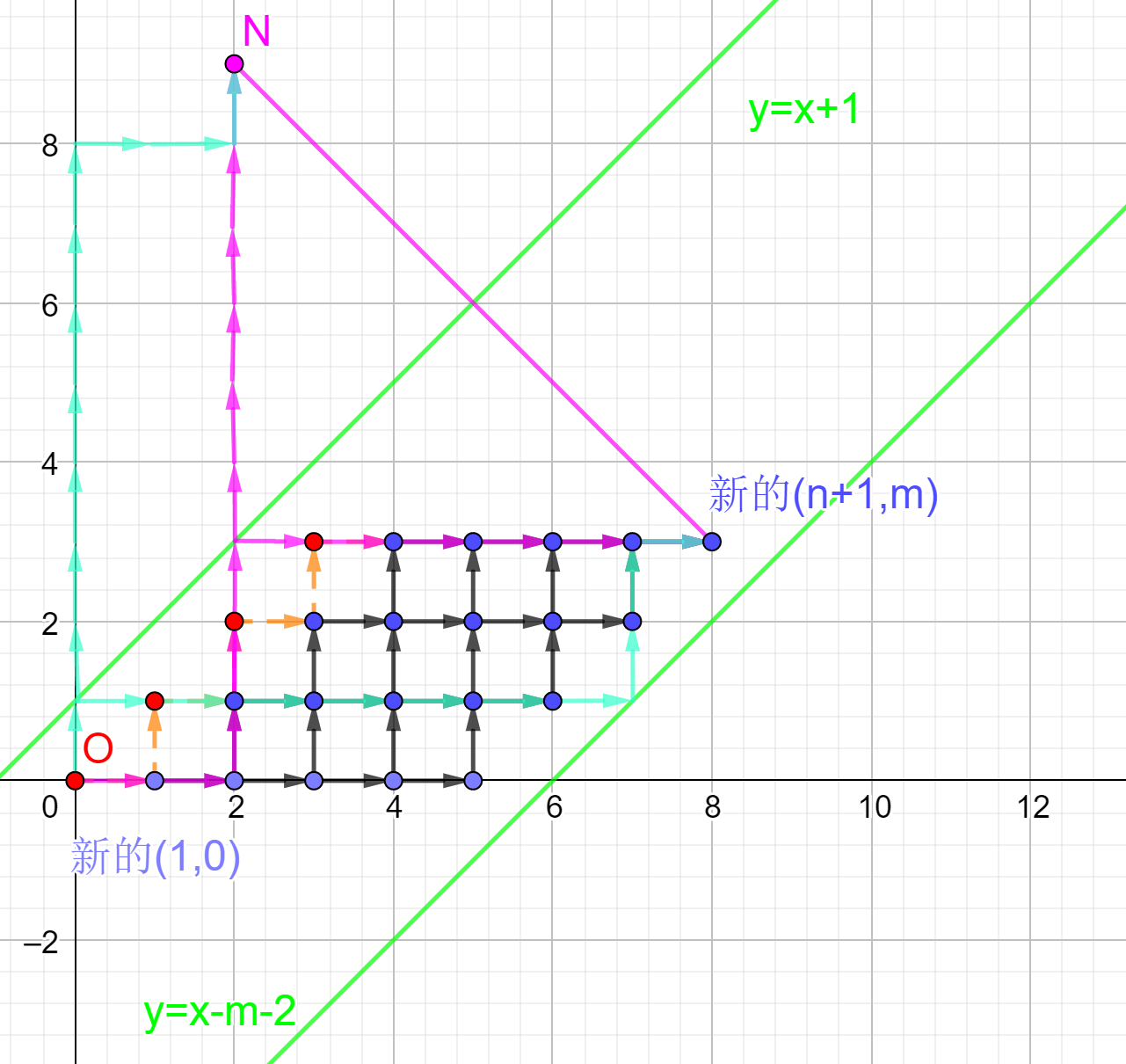
这样我们就可以计算了。容斥一下，答案就是 (dbinom {x_T+y_T}{x_T}- exttt{先到a的路径数}- exttt{先到b的路径数})。减去先到 (a) 的路径数，我们只需要减去以 (a,ab) 结尾的方案，加上以 (ba,bab) 结尾的方案，减去(ldots)

预处理阶乘的复杂度是线性的；而对称过程，每次的对称距至少增加 (1)，所以复杂度也是不超过线性的。所以总时间复杂度是线性的，空间复杂度也是线性的。

Code

#include <bits/stdc++.h>

#define il inline
#define ll long long
const int N=3e6+5,P=1e9+7;

int n,m,fac[N],ans;

il int ksm(int a,int b){int res=1; for ( ; b; b>>=1,a=(ll)a*a%P) if (b&1) res=(ll)res*a%P; return res;}

il int C(int x,int y){return x<0||y<0?0:(ll)fac[x+y]*ksm(fac[x],P-2)%P*ksm(fac[y],P-2)%P;}

il void trans(int &x,int &y,int a){std::swap(x,y),x-=a,y+=a;}

int main()
{
    scanf("%d%d",&n,&m); int i,x,y;
    for (i=fac[0]=1; i<N; i++) fac[i]=(ll)fac[i-1]*i%P;

    for (x=n+m+1,y=n,ans=C(x,y); x>=0&&y>=0;) trans(x,y,1),ans=(ans-C(x,y)+P)%P,trans(x,y,-m-2),ans=(ans+C(x,y))%P;
    for (x=n+m+1,y=n; x>=0&&y>=0; ) trans(x,y,-m-2),ans=(ans-C(x,y)+P)%P,trans(x,y,1),ans=(ans+C(x,y))%P; printf("%d
",ans);

    return 0;
}

类似题目

简要题意

给定 (N,m)，对于每个 (n=1sim N)，求有多少个长度为 (2n) 的环，满足：

1. 环中的每个元素都是 (1sim m) 的整数；
2. 环上任意相邻的两个数之差的绝对值都是 (1)。

结果对 (998244353) 取模，(1le n,mle 10^5)。

题解

有一个显然的 (O(Nm^2)) 的 DP 做法，我们枚举起点 ((0,x))，则终点必是 ((2n,x))，做一遍 (O(Nm)) 的 DP 即可。

我们考虑同上一题一样的，把这些转移放到坐标轴上看，可以发现答案就是从 ((0,x)) 为起点，只能向右上或者右下走，并且不能碰到直线 (a:y=0) 与 (b:y=m+1)，到 ((2n,x)) 的路径个数。

同之前一样，做对称变化，得到如下过程：
不翻折的，从 ((0,i)) 到 ((2n,i))，贡献是 (dbinom {2n}ncdot m)；
以 (a) 或 (b) 为中心翻折的，从 ((0,i)) 到 ((2n,-i))，贡献是 (-sum_{i=1}^m dbinom {2n}{n+i}) 的；
以 (ab) 或 (ba) 为中心翻折的，从 ((0,i)) 到 ((2n,2m+i+2))，贡献是 (dbinom {2n}{n+m+1}cdot m) 的。
(ldots)

---

你发现，对于 (dbinom {2n}i)，只有满足 (iequiv npmod{m+1}) 时它的系数是 (m)，而其他位置的系数都是 (-1)。又因为 (sum_{i=0}^{2n} dbinom {2n}i=2^{2n})，所以答案就是：

[left(sumlimits_{iequiv npmod{m+1}}{dbinom {2n}i} ight)cdot m-left(sumlimits_{i otequiv npmod{m+1}}{dbinom {2n}i} ight)=left(sumlimits_{iequiv npmod{m+1}}{dbinom {2n}i} ight)cdot (m+1)-sumlimits_{i=0}^{2n}{dbinom {2n}i}=left(sumlimits_{iequiv npmod{m+1}}{dbinom {2n}i} ight)cdot (m+1)-2^{2n} ]

这样就可以单次 (Oleft(dfrac nm ight)) 计算了。

接下来考虑对 (m) 根号分类，对于 (m>sqrt{N}) 的，可以直接用上面的算法做；而对于 (mle sqrt{N}) 的，我们做一个 DP，维护 (g_i=sumlimits_{jequiv ipmod{m+1}} dbinom{n}j)，单次转移时 (O(m)) 的，用滚动数组优化空间。

这样子时间复杂度就是 (Oleft(Nsqrt{N} ight)) 的，空间复杂度是 (O(N)) 的。

Code

#include <bits/stdc++.h>
#define il inline
#define ll long long
const int N=2e5+5,P=998244353;

int n,m,o,f[2][N],fac[N],iac[N],mi[N],ans[N];

il int ksm(int a,int b){int res=1; for ( ; b; b>>=1,a=(ll)a*a%P) if (b&1) res=(ll)res*a%P; return res;}

il int C(int x,int y){return x<y||y<0?0:(ll)fac[x]*iac[y]%P*iac[x-y]%P;}

int main()
{
    scanf("%d%d%d",&n,&m,&o); int i,j,k=0;
    for (i=fac[0]=mi[0]=1; i<N; i++) fac[i]=(ll)fac[i-1]*i%P,mi[i]=2ll*mi[i-1]%P;
    for (iac[i=N-1]=ksm(fac[N-1],P-2); i; i--) iac[i-1]=(ll)iac[i]*i%P;
	
    if (m*m<=n)
    {
        for (f[0][0]=i=1; i<=n+n; i++) for (k^=1,j=0; j<=m; j++)
        {
            f[k][(j+1)%(m+1)]=(f[!k][j]+f[!k][(j+1)%(m+1)])%P;
            if (i&1^1) ans[i>>1]=((ll)f[k][i/2%(m+1)]*(m+1)-mi[i]+P)%P;
        }
    }
    else
    {
        for (i=1; i<=n; i++)
        {
            for (j=i%(m+1); j<=i+i; j+=m+1) ans[i]=(ans[i]+C(i+i,j))%P;
            ans[i]=((ll)ans[i]*(m+1)-mi[i+i]+P)%P;
        }
    }
    for (i=1; i<=n; i++) if (i==n||o) printf("%d
",ans[i]);
    
    return 0;
}

另一道类似题目——【集训队作业2018】count

简要题意（照抄原题面）

如果一个序列满足序列长度为 (n)，序列中的每个数都是 (1) 到 (m) 内的整数，且所有 (1) 到 (m) 内的整数都在序列中出现过，则称这是一个挺好序列。

对于一个序列 (A)，记 (f_A(l,r)) 为 (A) 的第 (l) 个到第 (r) ​个数中最大值的下标（如果有多个最大值，取下标最小的）。

两个序列 (A) 和 (B) 同构，当且仅当 (A) 和 (B) 长度相等，且对于任意 (ile j)，均有 (f_A(i,j)=f_B(i,j))。

给出 (n,m)，求有多少种不同构的挺好序列。答案对 (998244353)​ 取模。

(1le n,mle 10^5)。

题解

考虑对原序列建出笛卡尔树（不知道笛卡尔树的可以去搜一下），则两个序列同构当且仅当他们的笛卡尔树同构。又由于有 (m) 的限制，这转化到树上就是每个叶子到根路径上作为左儿子的点要小于 (m)。因为笛卡尔树和序列是一一对应的，于是问题转化为了求有 (n) 个节点且最长左链不超过 (m) 的笛卡尔树数量。

这个就是经典结论：求有多少条从 ((0,0)) 出发到 ((2n,0)) 的路径，满足只能向右上或者右下走，并且不能触碰到 (y=-1) 与 (y=m+1)。这个直接用之前的方法做即可。

时空复杂度显然都是线性的。

Code

#include <bits/stdc++.h>
#define il inline
#define ll long long
const int N=2e5+5,P=998244353;

int n,m,ans,fac[N];

il int ksm(int a,int b){int res=1; for ( ; b; b>>=1,a=(ll)a*a%P) if (b&1) res=(ll)res*a%P; return res;}

il void flip(int &x,int &y){x=m-x,y=-y-2,std::swap(x,y);}

il int C(int x,int y){return y<0||x<y?0:(ll)fac[x]*ksm(fac[y],P-2)%P*ksm(fac[x-y],P-2)%P;}

int main()
{
    scanf("%d%d",&n,&m); if (n<m) return puts("0"),0; n+=n,m+=m+2; int i,x=-2,y=m;
    for (fac[0]=i=1; i<N; i++) fac[i]=(ll)fac[i-1]*i%P;
	
    for (i=P-1,ans=C(n,n/2); x>=-n||y<=n; i=P-i,flip(x,y))
	ans=(ans+(ll)i*C(n,x+n>>1)+(ll)i*C(n,y+n>>1))%P;
    printf("%d
",ans);
	
    return 0;
}