最近看了基于布尔网络的基因调控网络(GRN)的一些论文,来总结一下。这三篇论文比较散,不是该方向中的基石,作为了解一些基础布尔网络GRN及其应用即可。
1. An efficient approach towards the source-target control of Boolean networks[1]
借用这篇文章的一些内容,对布尔网络做一些基础介绍:

首先,布尔网络由布尔变量x(0/1的值,有时候会增加-1的值)和布尔方程f(元素之间与或非的关系)构成,可以等价为一个有向图,元素对应节点,方程分解为不同的边。
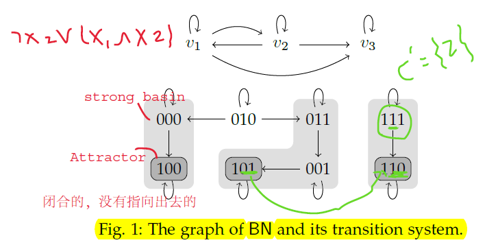
用上图来解释,v1 node对应的方程如左边红字所示,v1的布尔方程只有x1和x2两个变量组成。结合有向图,v1的输入来自v1和v2 nodes,表明v1只受v1和v2两个node调控。
这篇文章中,布尔网络的动态性指的是异步更新机制(还有其他更新方式),也就是每步只更新一个变量。布尔网络的动态性会生成状态转移图或叫转移系统(TS),如上图中的下半部分所示,整个系统只有三个变量,所以每个状态只有三个元素,根据更新情况绘制箭头指向。在状态转移图中介绍两个重要概念,吸引子(Attractor):如上图中深灰色的状态,是系统最后的稳态,没有指向其他状态的状态。强Basin(strong basin):浅灰色的区域,该区域中的节点只能唯一到达一个吸引子,如‘010’状态既可以到达‘100’又可以到达‘101’,其不属于强basin。
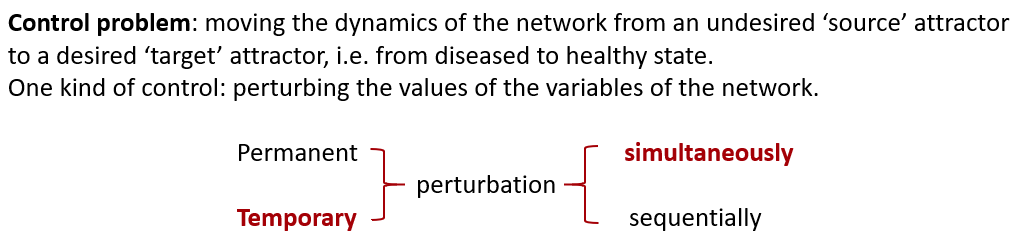
这篇文章主要属于控制问题,属于上面这个树状图方法的一个子集。这个问题是说如何将网络状态从一个不期望的‘source’ attractor(源稳态)引导到一个期望的‘target’ attractor(目的稳态),如将癌变的细胞改变为正常细胞。一种控制放式是通过增加扰动来实现,扰动网络中变量的值。作者将扰动方式分为上图中的四种,本文研究暂时性同时扰动。
This paper problem: The minimal simultaneous single-step source-target control problem for Boolean networks.
Goal: Given an asynchronous Boolean network, calculate the minimum number of nodes that driving the system from an initial state to a steady state in the perturbation. 这篇文章的主要目的是计算驱动系统从初态到末态最少需要扰动几个节点。如第一张图中的状态转移图所示,如果说将系统从状态‘101’改变到‘110’,明显需要扰动两个节点才可以(hamming距离是2),但实际上我们只需要扰动一个节点就够了,只扰动中间节点,我们得到状态‘111’,在强basin中,它最终一定会到稳态attractor‘110’中。这个在实际中的意义是扰动节点数越少意味着对生物体副作用越小,如服药进行扰动。
![]()
Key idea: decomposition-based method. (“divide and conquer” strategy)。这篇文章的方法主要是利用分治法对通用方法的改进,方法的输入输出如下:

如前面我们所分析所得,找strong basin是关键,这篇文章在global方法的基础上利用分治的思想,先找local的,最后再合并成为global的,并证明了其方法的正确性,也通过了案例研究验证。
Case study: Compare global method, decomposition-based method and corresponding optimized version on 6 real-life and 3 randomly generated Boolean networks. The results are identical and quite small(扰动节点个数)。
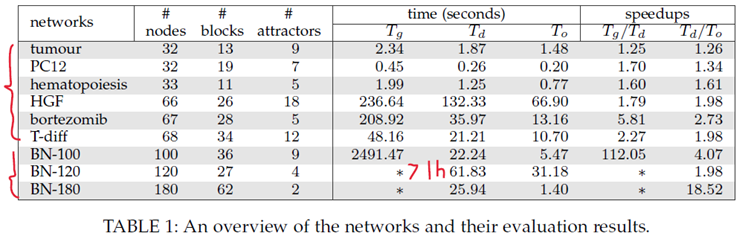
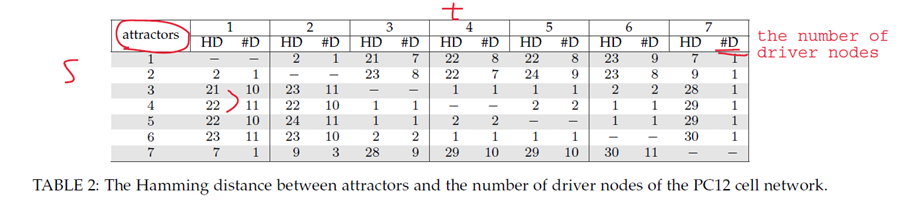
我们可以看到基于decomposition的方法减少了时间,且和global的方法结果一致,并且找到的驱动节点个数也是比较少的(上图中的#D)。
2. Modeling signaling‐dependent pluripotency with Boolean logic to predict cell fate transitions[2]
这篇文章主要是基于boolean network的建模文章。
Goal: Build a model to predict the GRN of PSCs responds to input signals.
Key idea: the model based on two strategies: R-ABS and SCCs.

Case: construct Mouse ESC-GRN, simulate the response of cells towards 5 combinations of signaling paths. mESC-GRN: 29 genes, 105 regulated relationships, 7 signal paths, 24 regulations of downstream.
Metrics: pluripotency, susceptibility, sustainability.
方法的输入输出如下:

3. ATLANTIS-Attractor landscape analysis toolbox for cell fate discovery and reprogramming[3]
这篇文章主要设计了一款基于matlab的带GUI的软件ATLANTIS来分析布尔网络的attractor landscape,并在4个已经发布的cases上做了验证。
主要的方法是将网络的动态性(节点状态转移机制)分为两种方法建模:deterministic model(closed,no external noise)和 probabilistic model(open,hosting external noise)
DA:
1. 第一种是基于权重的方法:
![]()
w是权重矩阵,b是basal expression value,f是符号函数(+1,0,-1)。
栗子:

权重就是GRN对应的有向图上的边权,+代表激活,-代表抑制。
DA过程的pipeline入下:

初始状态可以在状态空间中exhaustive采样,也可以随机采样或者用户自定义。
2. 第二种是基于规则的方法:
这里我理解就是类似bool方程这种对节点的规则,只不过这里用真值表存储。用真值表会更灵活一些。
栗子:
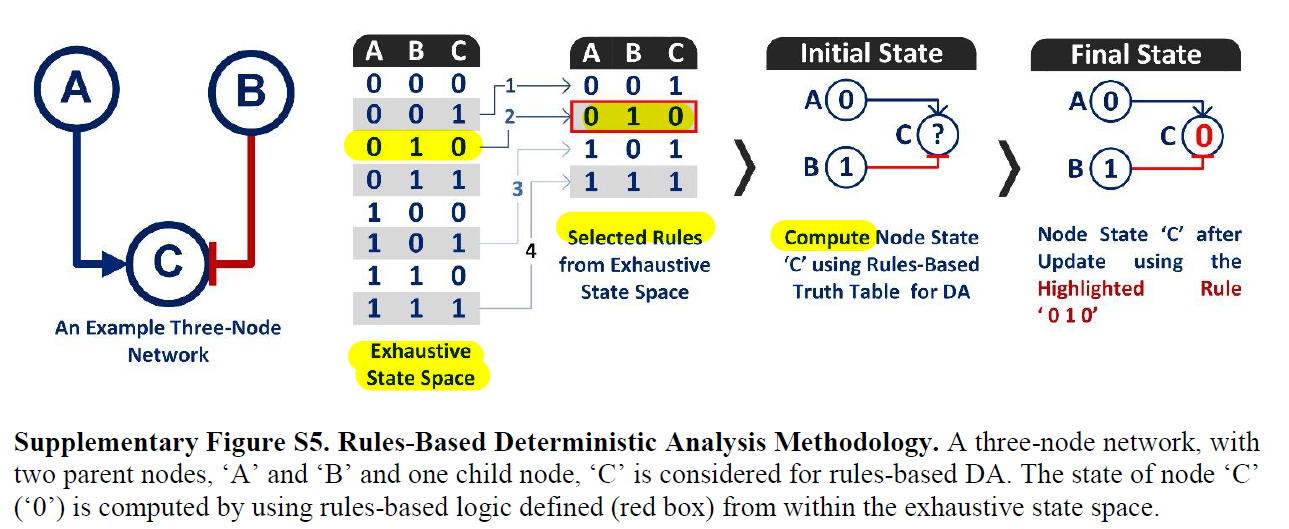
PA:
PA方法中网络状态转移是马尔可夫模型,下一步只与当前状态有关,不依赖于之前的状态,状态转移不是具体的值而是一定的概率,所以关键是如何表示状态转移概率。
然后通过一系列的建模得到了网络状态转移概率矩阵(具体参看原论文的supplement),最后用Pi(t+1)=Pi(t)近似已经达到稳态,最终画出的landscape是状态的landscape,来衡量状态的稳定性。
PA过程的pipeline入下:
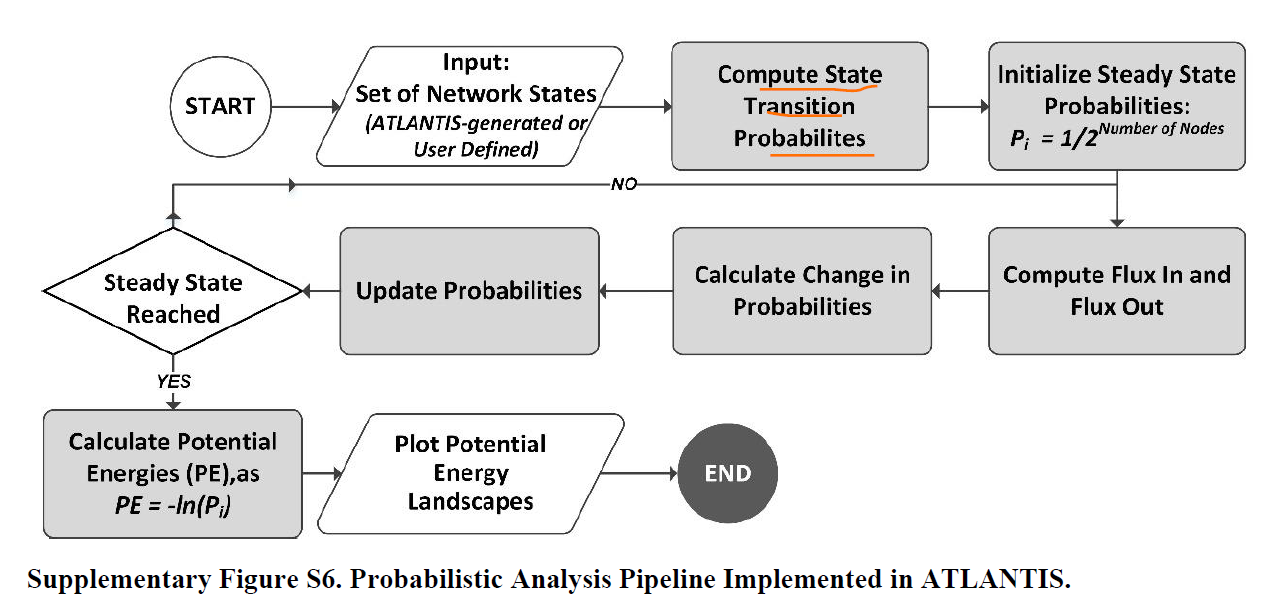
最后说一下attractor landscape的绘制,因为状态空间是高维的,如节点个数是n,就是n维,而landscape是3维的,所以需要降维,这里介绍了两种mapping的方法,Naive mapping和Sammon mapping。Naive mapping就是不考虑稳态之间的空间距离,将其映射到笛卡尔平面,Sammon mapping就是在投影之前将相关网络状态聚类到一起。
本文中提到的几种landscape:probability landscape;potential energy landscape(PE)(基于-lnP计算出的quasi-potential);cell fate landscape(CFL)(将attractor和对应细胞状态联系在一起,如phenotype)
Case 1: Decoding Yeast Cell Cycle Progression using Attractor Landscape Analysis
第一个case使用PA的方法可以得到酵母菌细胞周期发展的类型轨迹,中间阶段都代表不同的稳态(attractor)(由1个或多个网络状态组成)。
Case 2: Reprogramming P53-mediated Apoptosis in MCF-7 Breast Cancer Cell Lines
这里使用DA的方法进行癌症药物筛选,如在没有药物干预及不同药物及其组合干预后的情况。在没有药物干预时,只有一个attractor,basin大小为1,说明所有细胞都会处于这一状态,该状态对应细胞增殖。在用药后,预测细胞凋亡的情况。
Case 3: Investigating the Evolution of Cell Fate Landscape during Colorectal Tumorigenesis
该例使用DA的方法分析结直肠癌中一些突变因素影响。增加突变因素后,正常增殖的attractor的basin size开始逐渐减小,接着又分析了异常增殖的attractor,其size逐渐增大。
Case 4: Discovering Cell Fate Outcomes in HCT-116 Cells and their Reprogramming upon Inhibition of Various Nodes in its Network
该案例通过抑制药物靶点节点(node)观察细胞命运来得到癌症治疗药物的作用。(预测药物诱导细胞重编程)
Ref:
[1]. DOI 10.1109/TCBB.2019.2915081, IEEE/ACM Transactions on Computational Biology and Bioinformatics. ‘An efficient approach towards the source-target control of Boolean networks’, in press.
[2]. Yachie‐Kinoshita A, Onishi K, Ostblom J, et al. Modeling signaling‐dependent pluripotency with Boolean logic to predict cell fate transitions[J]. Molecular systems biology, 2018, 14(1): e7952.
[3]. Shah O S, Chaudhary M F A, Awan H A, et al. ATLANTIS-Attractor landscape analysis toolbox for cell fate discovery and reprogramming[J]. Scientific reports, 2018, 8(1): 1-11.