Ordered Fractions
顺序的分数
Consider the set of all reduced fractions between 0 and 1 inclusive with denominators less than or equal to N.
Here is the set when N = 5:
0/1 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1/1
Write a program that, given an integer N between 1 and 160 inclusive, prints the fractions in order of increasing magnitude.
输入一个自然数N
请写一个程序来增序输出分母小于等于N的既约真分数
PROGRAM NAME: frac1
INPUT FORMAT
One line with a single integer N.
SAMPLE INPUT (file frac1.in)
5
OUTPUT FORMAT
One fraction per line, sorted in order of magnitude.
SAMPLE OUTPUT (file frac1.out)
0/1 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1/1
最终 决定 以一道 刚做出来的 USACO 比较简单的题 开始 我的 第一篇随笔
希望 cnblogs 能陪伴我 走过 崎岖的 NOIP 之路
好了 言归正传：
这道题 好像与 法里数列 有关 可是 我越看 越迷茫的说
算了 先摘录下来吧：
/*【来自Wikipedia】
数列长度
n阶的法里数列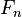
包含了较低阶的法里数列的全部项，特别是它包含
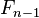的全部项，和与n互质的每个数的相应分数。所以
包含了
和分数1⁄6及5⁄6。对大于1的n，其法里数列的中间项必定是1⁄2。
从上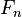，和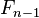的长度的关系，可以用欧拉函数
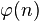描述：
。
从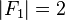
这项资料，可以推导出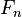的长度公式：
。
的渐近行为是：
。
数列邻项
法里数列的相邻分数项有下述性质：
若a⁄b和c⁄d是法里数列的邻项，而有a⁄b < c⁄d，则它们之差c⁄d − a⁄b是1⁄bd。由于
，
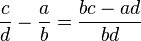上文就等于是说
- bc − ad = 1。
例如1⁄3和2⁄5在中是邻项，它们之差为1⁄15。
这结果的逆命题也成立。若
- bc − ad = 1，
其中a,b,c和d为正整数，及有a < b和c < d，则a⁄b和c⁄d在阶为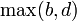
的法里数列中是邻项。
若p⁄q在某法里数列的邻项是a⁄b和c⁄d，及
- a⁄b < p⁄q < c⁄d，
则p⁄q是a⁄b和c⁄d的中间分数。换句话说，
。
又若a⁄b和c⁄d在某法里数列是邻项，则当法里数列的阶增加，它们间出现的第一项是
，
而这项第一次出现在b+d阶的法里数列中。
例如在1⁄3和2⁄5间出现的第一项是3⁄8，在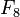
出现。
Stern-Brocot树是一个数据结构，显出如何从0 (= 0⁄1)和1 (= 1⁄1)开始，以取中间分数来构成法里数列。
法里数列中的邻项分数，它们的连分数表示形式也密切相关。每个分数都有两个连分数表示，一个的尾项为1，另一个则大于1。考虑p⁄q，它第一次于
出现。以连分数表示为
![[0;a_1, a_2, ..., a_{n-1}, a_n, 1]](http://upload.wikimedia.org/wikipedia/zh/math/e/4/e/e4e64237e042e293b2cbfc3efeca16fd.png)
，或![[0;a_1, a_2, ..., a_{n-1}, a_n + 1]](http://upload.wikimedia.org/wikipedia/zh/math/3/4/4/344a4b511ad603e39053ad9851520c8e.png)
，
则p⁄q在中最接近的邻项（这是两邻项中分母较大的）表示为连分数是
![[0;a_1, a_2, ..., a_n]](http://upload.wikimedia.org/wikipedia/zh/math/c/e/1/ce15da85862029f202c099b2064b1e33.png)
，
而另一邻项则会表示为
![[0;a_1, a_2, ..., a_{n-1}]](http://upload.wikimedia.org/wikipedia/zh/math/b/0/2/b023c018724d1c33107b64ed59ccb65d.png)
。
例如3⁄8有两个连分数表示：[0;2,1,1,1]和[0;2,1,2]，而它在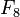中的邻项为2⁄5，可写成[0;2,1,1]；和1⁄3，可写成[0;2,1]。*/
中间貌似 提到了一个 Stern-Brocot树
所以 这个程序 好像就是 关于树型结构的
1 #include<stdio.h> 2 FILE*in,*out; 3 void pre(int x1,int x2,int y1,int y2,int n) 4 { 5 if(y1+y2>n)return ; 6 pre(x1,x1+x2,y1,y1+y2,n); 7 fprintf(out,"%d/%d\n",x1+x2,y1+y2); 8 pre(x1+x2,x2,y1+y2,y2,n); 9 } 10 int main() 11 { 12 int n; 13 in=fopen("frac1.in","r"); 14 out=fopen("frac1.out","w"); 15 fscanf(in,"%d",&n); 16 fprintf(out,"0/1\n"); 17 pre(0,1,1,1,n); 18 fprintf(out,"1/1\n"); 19 fclose(in); 20 fclose(out); 21 return 0; 22 }
说实话 我没看懂 然后 求人不如求己
1 #include <stdio.h> 2 #include <math.h> 3 struct{ 4 int fz; 5 int fm; 6 }a[161],temp; 7 void qsort(int low,int high) 8 { 9 if(low>=high)return; 10 int i=low,j=high; 11 temp=a[(low+high)/2]; 12 a[(low+high)/2]=a[low]; 13 while(i<j) 14 { 15 while(i<j&&a[j].fz*temp.fm>a[j].fm*temp.fz)j--; 16 if(i<j)a[i]=a[j]; 17 while(i<j&&a[i].fz*temp.fm<=a[i].fm*temp.fz)i++; 18 if(i<j)a[j]=a[i]; 19 } 20 a[i]=temp; 21 qsort(low,i-1); 22 qsort(i+1,high); 23 } 24 int main() 25 { 26 freopen("frac1.in","r",stdin); 27 freopen("frac1.out","w",stdout); 28 long n,i,j,t,k; 29 int sign=1; 30 scanf("%ld",&n); 31 printf("0/1\n"); 32 k=1; 33 for(i=2;i<=n;i++) 34 { 35 j=1; 36 while(j<i) 37 { 38 //x=(int)sqrt(i)+1; 39 sign=1; 40 for(t=2;t<=i;t++) 41 { 42 if(j%t==0&&i%t==0){ 43 sign=0; 44 break; 45 } 46 } 47 if(sign) 48 { 49 a[k].fz=j; 50 a[k].fm=i; 51 k++; 52 } 53 j++; 54 } 55 } 56 qsort(1,k-1); 57 for(i=1;i<=k-1;i++) 58 printf("%ld/%ld\n",a[i].fz,a[i].fm); 59 printf("1/1\n"); 60 return 0; 61 }
注意的是，中间的 for(t=2;t<=i;t++) 这句 我原先写的是 t<=(int)sqrt(i);但是 后来发现 这样 会实现不了 “既约”换句话说 就是 最后会输出很多 非最简分数
整体思路是，先用一个 for（限制了分母不超过n的条件）和while（限制了真分数和既约的条件）把所有符合条件的 fractions 的分子分母 分别放到一个结构体中 然后 用 快排 实现ordered
其中 a[j].fz*temp.fm>a[j].fm*temp.fz 是为了避免 double小数存分数时的误差
因为在最后一遍循环时 k被多加了一次 所以 qsort(1,k-1);
输出的时候 加的 printf 是特殊处理0/1和1/1两个分数
That's all,
that's a new beginning.