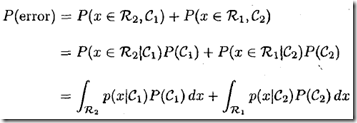NNPRChap1 统计模式识别（9）决策边界

当满足下面条件时将特征向量x付给类Ck时错分概率最小

                            （1）

由于边缘概率P(x)与类无关，因此上式转为

                      （2）

上面的操作就好像将特征空间划分成许多决策区域 ，当特性向量录入区域 时，则将其非给类 。这些区域无需是连续的。这些区域间的边界就是决策边界，或称为决策面。

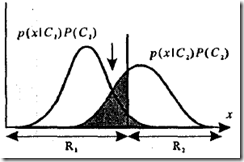
下面通过单维特征空间两类问题来说明如何确定最佳决策面，示意图如下

                        图.1

错分发生在将一个新数据归为C1，而其实际类别为C2（对应上图竖线右边黑色部分，以及下式右边第一项）；将一个新数据归为C2，而其实际类别为C1（对应上图竖线作边黑色部分，下式右边第二项），其发生概率为：

                           （3）

由图1可明显看出，当决策面（对应黑色竖线）位于两概率密度曲线交汇处时，黑色部分面积最小，也就是错分概率最小。此时采取的决策准则恰恰就是本文开头描述的将特征向量赋给后验概率最大的那个类。

1.判决函数（Distriminant funtions）

分类问题也可进一步抽象为为通过判决函数集合 ，将输入向量赋给类Ck，如果

                      

前面介绍的方法只不过是 时的特例。

可见，y(x)的大小唯一决定类的归属。同时， 可替换为 ，只要 是单调函数，此时决策面不会变化。例如，可采用对数变化，保证不影响结果。