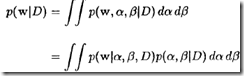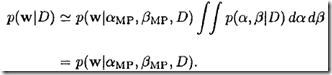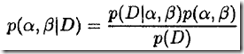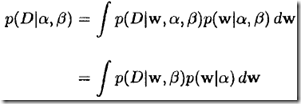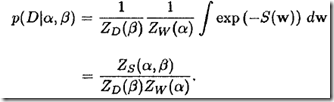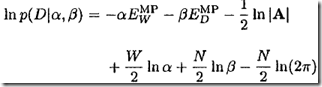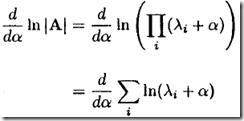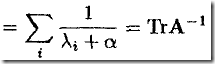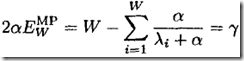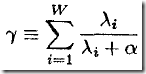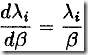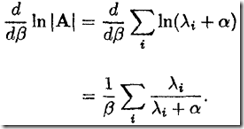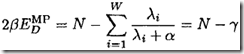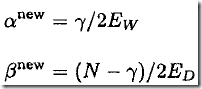前面假定超参数![]() 和
和![]() 是已知的,实际上这不太可能,只是有些情况下对噪声水平
是已知的,实际上这不太可能,只是有些情况下对噪声水平![]() 有些了解。我们也知道,正确的贝叶斯方法在处理这些未知参数时,就是对它们积分,这样最终预测函数就与它们无关了。例如,网络权重的后验分析计算方法如下
有些了解。我们也知道,正确的贝叶斯方法在处理这些未知参数时,就是对它们积分,这样最终预测函数就与它们无关了。例如,网络权重的后验分析计算方法如下
要解上面问题,方法还是那两种套路:1)解析方法:通过积分直接计算式1。留到本章第5节来介绍;2)近似方法:MacKay(1992a,1992d)研究此问题。这里先学习一下后者。
1)假设
在
附近呈现尖峰状,这样式1可近似为下式。也就是说,先求解
找到
和
的最大后验概率值
,然后直接带入下式计算。
2)那么
怎么求呢,还是利用贝叶斯准则构造下式求解。注意,这里要选择合适的先验
,因为它代表了超参数的先验,因此也称为超先验(hyperprior)。
1)首先,如何选择先验
呢?当没有任何概念时,选择的先验要所有参数值重要度相同,称为无信息先验。实际上,
和
是尺度参数(scale parameters),因为它们分别决定
和噪声的尺度。这里,因为没有不知道什么值合适,因此假设超先验
对
和
值不敏感。
到此,大家是不是能体会到一点层次化求解的意思呢?第一层求权重的分布(式1);第二层求超参的分布;且第二层中的置信度![]() 是前一层贝叶斯公示中的分母。这种结构就是一个层次化模型(hierarchical models,这其实也是目前很热的Graphical Modes研发方向搞的内容。
是前一层贝叶斯公示中的分母。这种结构就是一个层次化模型(hierarchical models,这其实也是目前很热的Graphical Modes研发方向搞的内容。
带入式4得
其中
在选定的先验和噪声模型下的解也在前面讨论过了:
;
3)得到置信度的log
C)从而,有
a)
是权重的二次函数(如线性网络,误差为SSE)时,赫森矩阵是常数,上面假设成立,式6正确。
对于上的结果,前人(Gull, 1989).已经给出了简单优美的解释:最大可能权重![]() 的值代表了在多大程度上权重值来自于数据中的信息,没有任何数据时,
的值代表了在多大程度上权重值来自于数据中的信息,没有任何数据时,![]() =0。。假设特征值为正,那么
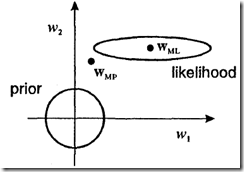
=0。。假设特征值为正,那么![]() 取值范围为(0,1)。它的几何解释为:旋转权重空间左边轴,以与赫森矩阵H的特征向量方向对齐。示意图1,圆环代表
取值范围为(0,1)。它的几何解释为:旋转权重空间左边轴,以与赫森矩阵H的特征向量方向对齐。示意图1,圆环代表![]() 的等高线(对应先验piror),椭圆代表
的等高线(对应先验piror),椭圆代表![]() 的等高线(对应似然likelihood)
的等高线(对应似然likelihood)
1)在
的方向上(图1中W1方向):式8中求和项接近于1;权重主要由数据决定。
2)在
的方向上(图1中W2方向):式8中求和项主要由
决定;权重主要由先验决定。
3)因此
度量了有效权重的个数,这些权重的值由数据决定而不是先验,因此也称为well-determined parameters
2)上面的东东会使式5在最大值处满足如下条件
到此,所有的分析都利用单高斯分布来近似权重的后验分布。这并不足够合理,因为对应非线性网络其正则化误差S(w)会有很多极小值。MacKay(1992d)采用的方法,是选择一系列特殊的权重![]() 来预测,它们对应于S(w)的特殊的极小点。因此,可以选取合适的
来预测,它们对应于S(w)的特殊的极小点。因此,可以选取合适的![]() 和
和![]() 值(不同的极小点可能会要求不同的值)。这时,式4的积分就不是对整个权重空间进行的,而是对这些极小点领域范围进行积分。
值(不同的极小点可能会要求不同的值)。这时,式4的积分就不是对整个权重空间进行的,而是对这些极小点领域范围进行积分。
上面的思想很好,具体如何实现呢,即如何找到最优![]() 和
和![]() 以及
以及![]() ?一个简单的方法就是迭代求解,由式7和9有
?一个简单的方法就是迭代求解,由式7和9有
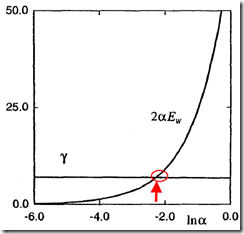
这里,进一步利用Chap10第3节中图3的例子来讲述另一种方法,即利用置信度方法(evidence approach)来确定![]() 和
和![]() ,见图2和图3。对比两图,可发现:
,见图2和图3。对比两图,可发现:
2)注:两图中
设为其真值;
值是通过利用精确解析方法(exact analytical methods)计算赫森矩阵,然后找到其特征值谱而得到的。
图2(横坐标是lna,横线对应r,曲线对应![]() ,
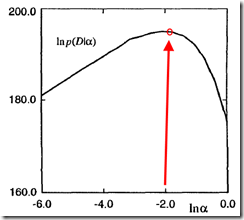
,![]() 设为其真值) 图3(横坐标是lna,曲线是a的logevidence(lnp(D|a)),
设为其真值) 图3(横坐标是lna,曲线是a的logevidence(lnp(D|a)),![]() 设为其真值)
设为其真值)