数字信号处理 － chap6 有限脉冲响应滤波器（1）基础

6.1 基础

非递归滤波器（有限脉冲响应滤波器，finite impulse response filter）仅取决与过去的输入，与输出无关

                                        （1）

其脉冲响应为有限项，因此称为有限脉冲响应滤波器（FIR滤波器）

               

FIR滤波器的设计就是选择合适的系数 以得到所需要的滤波器特性。一般，滤波器的滚降越陡峭，需要的系数也就越多。

6.2滑动平均滤波器

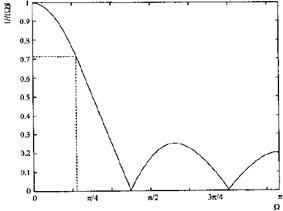
它计算数字采样序列的滑动平均值。

考虑一个五项滑动平均滤波器           

                     

它的传输函数 ，频响为

从下图中它的滤波器形状可证实滑动平均滤波器是低通滤波器。

6.3 相位失真

当正弦信号通过线性滤波器时，其幅度和相位都要改变。对于输入 ，输出为 ，输入频率和输出频率相同，但幅度和相位发生变换，其中 为滤波器在 处的增益， 为相位差。

由于信号中的不同频率分量通过滤波器产生的相位延迟不同，因此产生相位失真。要确保不产生相位失真的唯一办法就是保证不同频率分量通过滤波器时有相同的延迟。

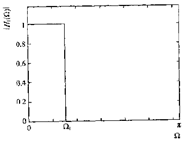
6.4 理想低通滤波器

理想低通滤波器的单边幅度响应：

        

产生理想低通滤波器的脉冲响应计算公式：

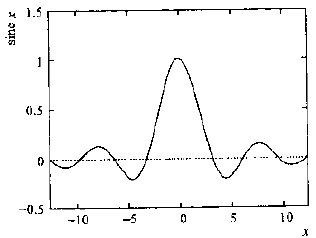
1）n=0时，脉冲响应表示为Sinc函数，其定义为 。Sinc函数的图形如下：

                  

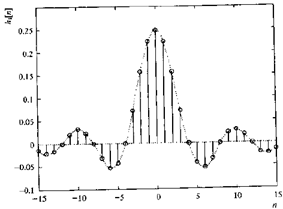
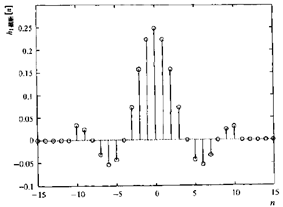
2）理想低通滤波器的脉冲响应如下图，它在每个方向上有无限个采样点，它的包络是Sinc函数

                      

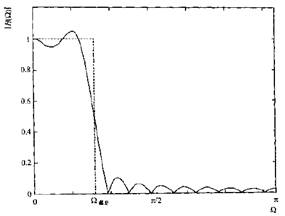
要设计一个理想低通滤波器并不是那么简单：

1）由于脉冲响应是非因果的（n＝0之前就存在，由上图可看出）。并且，n<0时的非零值无限多，它不能像滑动平均滤波器那样进行时移。

2）它有无限多项，因此不能转换为非递归差分方程。

最简单的解决办法就是截断脉冲响应值很小的采样点，从而变换有限长，能够位移且为因果的。

                            

截断后会对频率响应产生影响，滤波器形状不再是矩形。保留的采样点越多（忽略的信息越少），滤波器形状就越接近矩形。