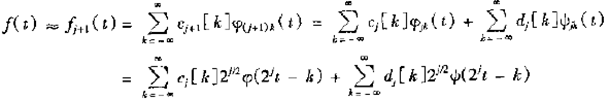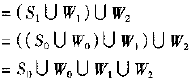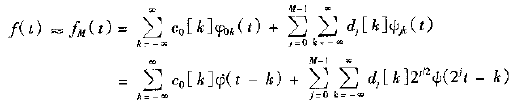8.3 信号编码
小波可将信号分解为基函数的尺度化和平移副本，因此可以用来对信号进行编码。当然，这首先要求该小波族的特性与被编码信号的特性相近；同时，应能用最小的尺度对信号中最细微的部分编码。要对函数f(t)编码，需要构造表达式如下。其中，j要足够大，从而尺度
足够小，以保证能够捕获重要的信号细节。
可被尺度为j的尺度函数完整描述的一族函数
属于Sj子空间。对于一个特定时间段那的Sj子空间中的信号编码，需要所有定义在该时间段的尺度为
的尺度函数的平移。
8.3.1 基于多尺度函数的编码
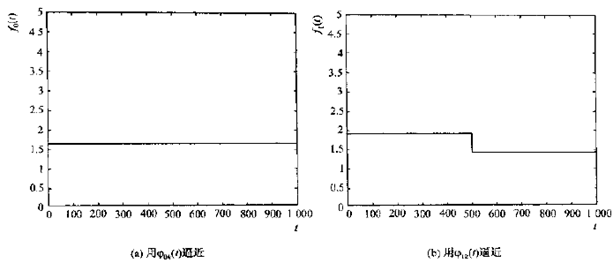
下面介绍通过尺度函数对信号进行编码的例子
1）待编码的信号形状与Haar小波接近，可用它来编码
2）随着j的增加，尺度函数越来越接近待编码的信号
3）在确定可接受的误差范围之后，就可以选择合适的尺度
4）图h中信号的近似表达为
。此时函数f(t)不属于子空间
，应为它不能被此尺度上的尺度函数所完全描述。
图1. 通过尺度函数对信号编码
8.3.1 基于小波函数的编码
虽然使用尺度函数能对信号进行编码，但使用小波的效率更高。
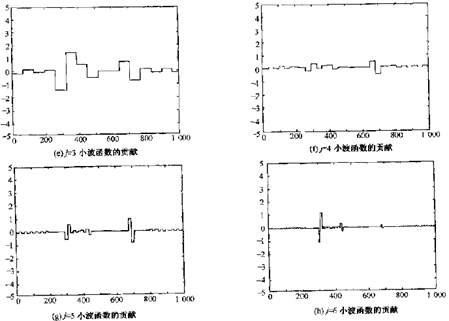
先看下面Haar小波图
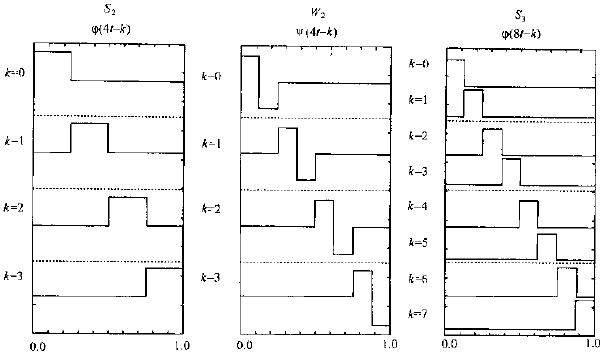
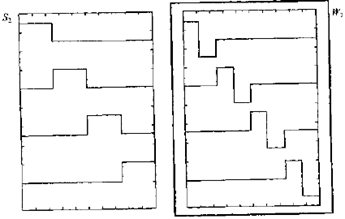
图2. 小波函数的贡献
1）前两列显示了函数
和
的波形，它们是j=2尺度上尺度函数的基和小波函数的基，分别覆盖子空间S2和W2
2）第3列是j=3时的尺度函数，覆盖子空间S3，
3）覆盖S2的函数不能组合出覆盖S3的函数，除非将其与覆盖W2的函数组合。
4）如图中第1行所示
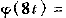
，小波函数
可描述任何能被尺度函数集
描述的信号，而这些信号不能被
基所描述。进而有，小波函数形成的子空间覆盖了两个相邻尺度的尺度函数所形成子空间的“差”。所以，
中的函数即可用
中的尺度函数编码，也可用
中的尺度函数和
中的小波函数来组合编码
（1）
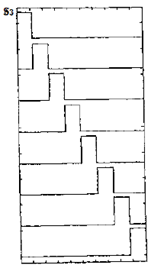
下图显示了对于Haar族的前几个尺度，要找出尺度间细节所需的小波函数。子空间S3总是被S2和W2的组合所覆盖，计为
，进而推广到其它尺度子空间有
（2）
根据式2，可知信号可用一个尺度函数和很多小波函数来编码，公式1可变为：
（3）
1）
由子空间
所覆盖
2）第1项依赖于
（j=0尺度上的尺度函数平移）
3）第2项
是j从0到M-1的小波函数的所有尺度和平移。
4）c0[k]和dj[k]是小波系数。所有这些构成了信号的离散小波变换。
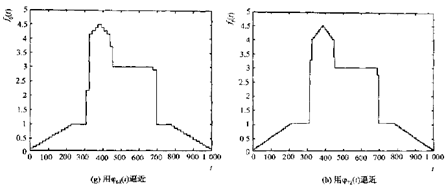
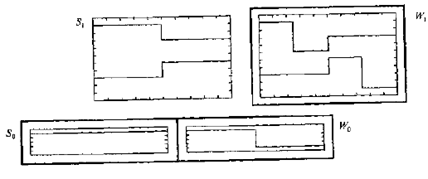
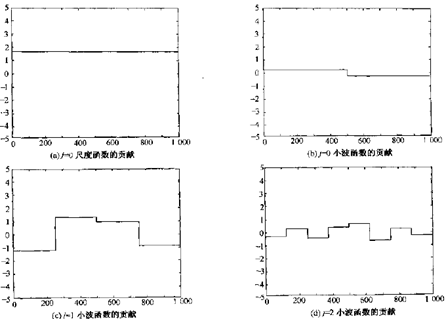
下图展示的是通过一个基尺度函数和一族小波函数重新对信号进行编码的结果，通过将尺度函数与期望数量的小波细节函数现价实现编码。图3中8个函数的和形成图4的信号，函数为
图3. 通过小波函数对信号编码
图4. 图3中尺度函数及各小波函数的和
8.4 多分辨率分析
前面介绍基于小波函数的信号编码时有公式3，这里重点介绍如何计算小波系数。
8.4.1 尺度函数的多分辨率分析
尺度函数
的重要特点是它可以表示成下一较细精度上的尺度函数加权和，即满足下面的多分辨率分析（multiresolution analysis，MRA）方程
（4）
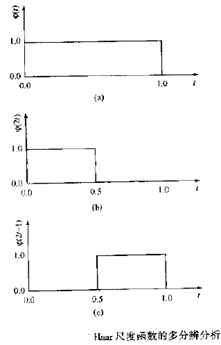
下面通过Haar小波来介绍上面的概念。如下图所示，
，从而得MRA方程
，其中
图3. Haar尺度函数的多分辨率分析
8.4.2 小波函数的多分辨率分析
小波函数
也能由尺度函数
的平移来建立，表达式也是一个MSA方程。这说明小波族中每个小波函数可以表达为下一较细精度上的尺度函数加权和。
（5）
至此，我们就清楚为什么父小波和母小波有那么多共同点。因为，小波函数由尺度函数确定，而尺度函数来做父小波。从这个意义上来说，福父小波决定了小波族中所有成员的特性。
下面同样以Haar小波为例来介绍上面概念。图4是Haar母小波，结合图3可知
，其MRA方程为
，其中
。
图4. Haar母小波
其它小波族同样服从MSA方程（式4、5），但是它们尺度函数和小波函数间的关系不如Haar族那么明显。