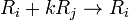单位阵(Identity Matrix)
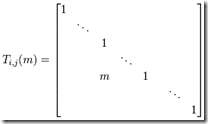
定义:单位阵是对角元素为1,其它元素为0的方阵。
性质:
AIn = A 且 InB = B
对称阵(symmetric matrix)
定义:对称阵为其转置和自身相等的方阵,即元素以主对角线((左上至右下)为轴进行对称,AT = A
斜对称阵(skew-symmetric matrix)
定义:对称阵为其转置和自身加法逆相等的方阵,AT = − A。
性质:
初等矩阵(Elementary Matrix)
接近问题时,常将复杂问题分解为一些基础模块。这里要介绍的就是如何将一个矩阵分解为一系列初等矩阵的乘积。
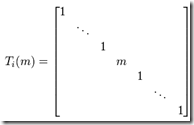
定义:一个 n 阶单位矩阵 E 经过一次初等行变换或一次初等列变换所得矩阵称为 n 阶初等矩阵。
初等矩阵分为3种类型,分别对应着3种不同的行/列变换。
性质:
- 1)
 ;| Tij | = − 1; | TijA | = − | A | 。
;| Tij | = − 1; | TijA | = − | A | 。
作用:左乘初等矩阵相当于对矩阵行进行初等变换;右乘初等矩阵相当于对矩阵列进行初等变换。
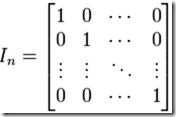
 。如下互换第i,j行
。如下互换第i,j行 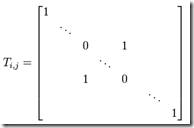
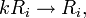 其中
其中