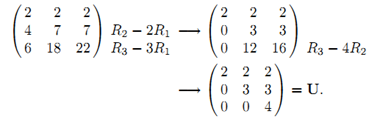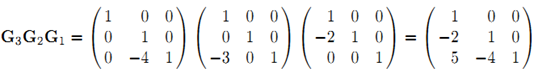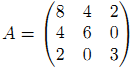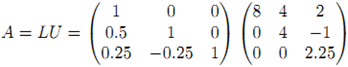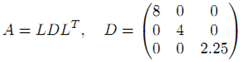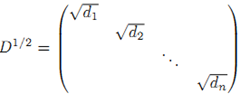1. LU分解
LU分解在本质上是高斯消元法的一种表达形式。实质上是将A通过初等行变换变成一个上三角矩阵,其变换矩阵就是一个单位下三角矩阵。这正是所谓的杜尔里特算法(Doolittle algorithm):从下至上地对矩阵A做初等行变换,将对角线左下方的元素变成零,然后再证明这些行变换的效果等同于左乘一系列单位下三角矩阵,这一系列单位下三角矩阵的乘积的逆就是L矩阵,它也是一个单位下三角矩阵。
下面以具体例子来说明。若AX=b是一个非奇异系统,那么高斯消元法将A化简为一个上三角矩阵。若主轴上没有0值,则无需交互行,因此只需进行第3类初等行变换(把第 i 行加上第 j 的 k 倍)即可完成此变换。例如
第3类行变换可以通过左乘相应的初等矩阵![]() 实现,对上例来说进行的3个变换就是相应初等矩阵的乘积。注意最右边是一个下三角矩阵L
实现,对上例来说进行的3个变换就是相应初等矩阵的乘积。注意最右边是一个下三角矩阵L
从而有![]() ,即
,即![]() 。因此A=LU,为一个下三角与一个上三角矩阵的乘积,因此称为LU分解。
。因此A=LU,为一个下三角与一个上三角矩阵的乘积,因此称为LU分解。
注意
1)U是高斯消元的结果,且对角线上是主元
2. LDU分解
LU分解存在不对称,因为L矩阵的主对角线元素为1,而U矩阵主对角线不为1。为了对此进行弥补,可U矩阵进一步做如下分解
这就是LDU分解,其中L和U是单位三角阵(主对角线都为1),D是对角阵。
下图说明了Walsh matrix的LDU分解
3. LDLT分解
当A是对称阵时,LDU分解为A=LDLT 。例子如下