Python Basics with Numpy

原链接

1 - Building basic functions with numpy

1.1 - sigmoid function

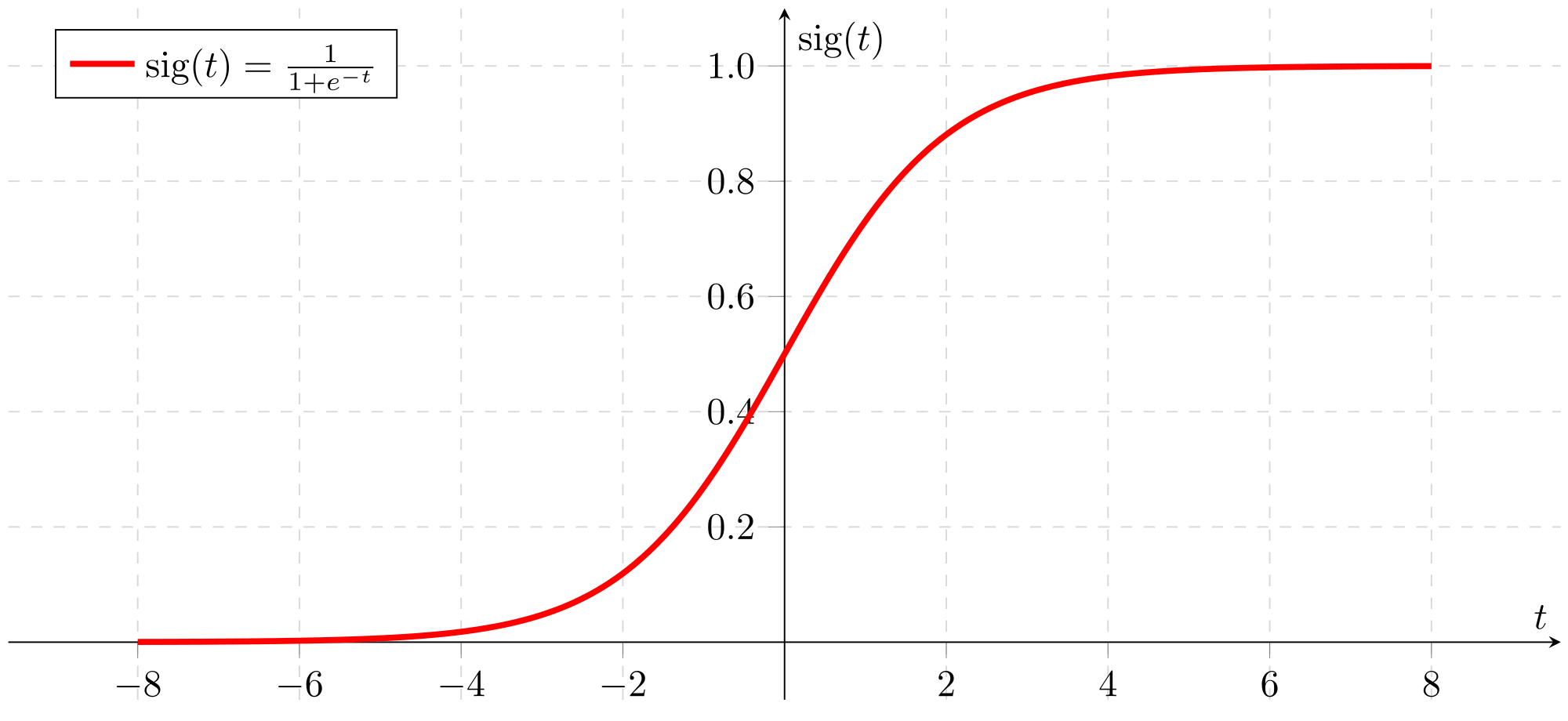
(sigmoid(x) = frac{1}{1+e^{-x}}) is sometimes also known as the logistic function. It is a non-linear function used not only in Machine Learning (Logistic Regression), but also in Deep Learning.

[ ext{For } x in mathbb{R}^n ext{, } sigmoid(x) = sigmoidegin{pmatrix} x_1 \ x_2 \ ... \ x_n \ end{pmatrix} = egin{pmatrix} frac{1}{1+e^{-x_1}} \ frac{1}{1+e^{-x_2}} \ ... \ frac{1}{1+e^{-x_n}} \ end{pmatrix} ag{1} ]

# GRADED FUNCTION: sigmoid

import numpy as np # this means you can access numpy functions by writing np.function() instead of numpy.function()

def sigmoid(x):
    """
    Compute the sigmoid of x

    Arguments:
    x -- A scalar or numpy array of any size

    Return:
    s -- sigmoid(x)
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    s = 1 / (1 + np.exp(-x))
    ### END CODE HERE ###
    
    return s

1.2 - Sigmoid gradient

[sigmoid\_derivative(x) = sigma'(x) = sigma(x) (1 - sigma(x)) ag{2} ]

# GRADED FUNCTION: sigmoid_derivative

def sigmoid_derivative(x):
    """
    Compute the gradient (also called the slope or derivative) of the sigmoid function with respect to its input x.
    You can store the output of the sigmoid function into variables and then use it to calculate the gradient.
    
    Arguments:
    x -- A scalar or numpy array

    Return:
    ds -- Your computed gradient.
    """
    
    ### START CODE HERE ### (≈ 2 lines of code)
    s = sigmoid(x)
    ds = s * (1 - s)
    ### END CODE HERE ###
    
    return ds

1.3 - Reshaping arrays

# GRADED FUNCTION: image2vector
def image2vector(image):
    """
    Argument:
    image -- a numpy array of shape (length, height, depth)
    
    Returns:
    v -- a vector of shape (length*height*depth, 1)
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    v = image.reshape(image.shape[0]*image.shape[1], image.shape[2])
    ### END CODE HERE ###
    
    return v

1.4 - Normalizing rows

Another common technique we use in Machine Learning and Deep Learning is to normalize our data. It often leads to a better performance because gradient descent converges faster after normalization. Here, by normalization we mean changing x to (frac{x}{| x|}) (dividing each row vector of x by its norm).

For example, if

[x = egin{bmatrix} 0 & 3 & 4 \ 2 & 6 & 4 \ end{bmatrix} ag{3} ]

then

[| x| = np.linalg.norm(x, axis = 1, keepdims = True) = egin{bmatrix} 5 \ sqrt{56} \ end{bmatrix} ag{4} ]

and

[x\_normalized = frac{x}{| x|} = egin{bmatrix} 0 & frac{3}{5} & frac{4}{5} \ frac{2}{sqrt{56}} & frac{6}{sqrt{56}} & frac{4}{sqrt{56}} \ end{bmatrix} ag{5} ]

# GRADED FUNCTION: normalizeRows

def normalizeRows(x):
    """
    Implement a function that normalizes each row of the matrix x (to have unit length).
    
    Argument:
    x -- A numpy matrix of shape (n, m)
    
    Returns:
    x -- The normalized (by row) numpy matrix. You are allowed to modify x.
    """
    
    ### START CODE HERE ### (≈ 2 lines of code)
    # Compute x_norm as the norm 2 of x. Use np.linalg.norm(..., ord = 2, axis = ..., keepdims = True)
    x_norm = np.linalg.norm(x, axis=1, keepdims = True)  # keepdims默认为False，那样算出来的x_norm的shape为(n,)，设为True后x_norm才是一个行向量，shape为(n,1)
    
    # Divide x by its norm.
    x = x / x_norm
    ### END CODE HERE ###

    return x

x = np.array([
    [0, 3, 4],
    [1, 6, 4]])
print("normalizeRows(x) = " + str(normalizeRows(x)))

normalizeRows(x) = [[ 0. 0.6 0.8 ]
[ 0.13736056 0.82416338 0.54944226]]

1.5 - Broadcasting and the softmax function

[ ext{for } x in mathbb{R}^{1 imes n} ext{, } softmax(x) = softmax(egin{bmatrix} x_1 && x_2 && ... && x_n end{bmatrix}) = egin{bmatrix} frac{e^{x_1}}{sum_{j}e^{x_j}} && frac{e^{x_2}}{sum_{j}e^{x_j}} && ... && frac{e^{x_n}}{sum_{j}e^{x_j}} end{bmatrix} ]

[ ext{for a matrix } x in mathbb{R}^{m imes n} ext{, $x_{ij}$ maps to the element in the $i^{th}$ row and $j^{th}$ column of $x$, thus we have: } ]

[softmax(x) = softmaxegin{bmatrix} x_{11} & x_{12} & x_{13} & dots & x_{1n} \ x_{21} & x_{22} & x_{23} & dots & x_{2n} \ vdots & vdots & vdots & ddots & vdots \ x_{m1} & x_{m2} & x_{m3} & dots & x_{mn} end{bmatrix} = egin{bmatrix} frac{e^{x_{11}}}{sum_{j}e^{x_{1j}}} & frac{e^{x_{12}}}{sum_{j}e^{x_{1j}}} & frac{e^{x_{13}}}{sum_{j}e^{x_{1j}}} & dots & frac{e^{x_{1n}}}{sum_{j}e^{x_{1j}}} \ frac{e^{x_{21}}}{sum_{j}e^{x_{2j}}} & frac{e^{x_{22}}}{sum_{j}e^{x_{2j}}} & frac{e^{x_{23}}}{sum_{j}e^{x_{2j}}} & dots & frac{e^{x_{2n}}}{sum_{j}e^{x_{2j}}} \ vdots & vdots & vdots & ddots & vdots \ frac{e^{x_{m1}}}{sum_{j}e^{x_{mj}}} & frac{e^{x_{m2}}}{sum_{j}e^{x_{mj}}} & frac{e^{x_{m3}}}{sum_{j}e^{x_{mj}}} & dots & frac{e^{x_{mn}}}{sum_{j}e^{x_{mj}}} end{bmatrix} = egin{pmatrix} softmax ext{(first row of x)} \ softmax ext{(second row of x)} \ ... \ softmax ext{(last row of x)} \ end{pmatrix} ]

# GRADED FUNCTION: softmax

def softmax(x):
    """Calculates the softmax for each row of the input x.

    Your code should work for a row vector and also for matrices of shape (m,n).

    Argument:
    x -- A numpy matrix of shape (m,n)

    Returns:
    s -- A numpy matrix equal to the softmax of x, of shape (m,n)
    """
    
    ### START CODE HERE ### (≈ 3 lines of code)
    # Apply exp() element-wise to x. Use np.exp(...).
    x_exp = np.exp(x)

    # Create a vector x_sum that sums each row of x_exp. Use np.sum(..., axis = 1, keepdims = True).
    x_sum = np.sum(x_exp, axis=1, keepdims=True)
    
    # Compute softmax(x) by dividing x_exp by x_sum. It should automatically use numpy broadcasting.
    s = x_exp / x_sum

    ### END CODE HERE ###
    
    return s

2 - Vectorization

传统实现方法：

x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]

### CLASSIC DOT PRODUCT OF VECTORS IMPLEMENTATION ###
dot = 0
for i in range(len(x1)):
    dot+= x1[i]*x2[i]

### CLASSIC OUTER PRODUCT IMPLEMENTATION ###
outer = np.zeros((len(x1),len(x2))) # we create a len(x1)*len(x2) matrix with only zeros
for i in range(len(x1)):
    for j in range(len(x2)):
        outer[i,j] = x1[i]*x2[j]

### CLASSIC ELEMENTWISE IMPLEMENTATION ###
mul = np.zeros(len(x1))
for i in range(len(x1)):
    mul[i] = x1[i]*x2[i]

### CLASSIC GENERAL DOT PRODUCT IMPLEMENTATION ###
W = np.random.rand(3,len(x1)) # Random 3*len(x1) numpy array
gdot = np.zeros(W.shape[0])
for i in range(W.shape[0]):
    for j in range(len(x1)):
        gdot[i] += W[i,j]*x1[j]

向量化实现：

x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]

### VECTORIZED DOT PRODUCT OF VECTORS ###
dot = np.dot(x1,x2)

### VECTORIZED OUTER PRODUCT ###
outer = np.outer(x1,x2)

### VECTORIZED ELEMENTWISE MULTIPLICATION ###
mul = np.multiply(x1,x2)

### VECTORIZED GENERAL DOT PRODUCT ###
dot = np.dot(W,x1)

2.1 - Implement the L1 and L2 loss functions

• L1 loss is defined as:

[egin{align*} & L_1(hat{y}, y) = sum_{i=0}^m|y^{(i)} - hat{y}^{(i)}| end{align*} ag{6} ]

# GRADED FUNCTION: L1

def L1(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L1 loss function defined above
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    loss = np.sum(np.abs(yhat - y))
    ### END CODE HERE ###
    
    return loss

• L2 loss is defined as

[egin{align*} & L_2(hat{y},y) = sum_{i=0}^m(y^{(i)} - hat{y}^{(i)})^2 end{align*} ag{7} ]

# GRADED FUNCTION: L2

def L2(yhat, y):
    """
    Arguments:
    yhat -- vector of size m (predicted labels)
    y -- vector of size m (true labels)
    
    Returns:
    loss -- the value of the L2 loss function defined above
    """
    
    ### START CODE HERE ### (≈ 1 line of code)
    loss = np.sum(np.dot((y - yhat), (y - yhat)))
    ### END CODE HERE ###
    
    return loss