题目
一个均匀绳子,长度为(L),质量为(m),下端刚好接触一个天平。现在开始自由下落。当天平上绳子的长度恰好为(x)时,求天平这时的读数
解法
(frac 12gt^2=xLeftrightarrow t=sqrt {frac {2x}g})
(v=gt=sqrt {2gx})
(FDelta t=Delta mvLeftrightarrow F=frac {Delta mv}{Delta t})
对于式子(frac {Delta m}{Delta t}),有两种解法:
①我:可以将其视作一种速度,对于当前极短时间内的速度(v)与以这种速度遍历整条绳子的时间(T=frac Lv),有(frac {Delta m}{Delta t}=frac mT)
②boshi:(Delta m=vcdot Delta t cdot frac xLcdot m),上下消元即可
最后各方式子汇合可得(F=frac {2gx}L),再算上原本在天平上的重量,最终答案为(frac {3gx}L)
题目
一个无穷网格,每条线段的电阻为 1 欧,求相邻两点之间的等效电阻的大小。
解法
假设一个大小为(1A)的电流从起点处流入,从各个无穷远处流出。由对称性,有(0.25A)的电流将会流过两点之间的线段。现在,再假设一个大小为(1A)的电流从各个无穷远处流入,从终点流出。由对称性,两点之间的线段仍然有(0.25A)的电流。现在,把两种情况叠加在一起看,大小为(1A)的电流从起点进去从终点出来,那么,两点间的线段就有(0.5A)的电流,电压为(0.5Acdot 1Ω=0.5V),等效电阻为(frac {0.5V}{1A}=0.5Ω)
题目
把大米扛起来往秤上倒,大米是以(q)的速度匀速流出。大米下落的高度是(h)。B 君要买质量为(m)的米。卖米的大爷看到秤的度数显示为(m)的时候,立刻停止了倒米。空中的米继续下落。问 B 君亏了还是卖米的大爷亏了。
解法
称量偏差:(m=frac Fg=frac {Delta mv}{Delta tg}=qsqrt {frac {2h}g})
空中剩余:(m=tq=sqrt{frac{2h}g}q)
所以谁也没亏
题目
将一个硬币抛起来,如果立起来的可能性为(frac 13),求硬币半径与厚度之间的关系
解法
网上(Matrix67)的解法是在二维平面意义下的错误解法,但为我们在三维意义下的正解提供了思路
首先二维平面意义下的解法是考虑矩形外接圆,再考虑弧长,如图
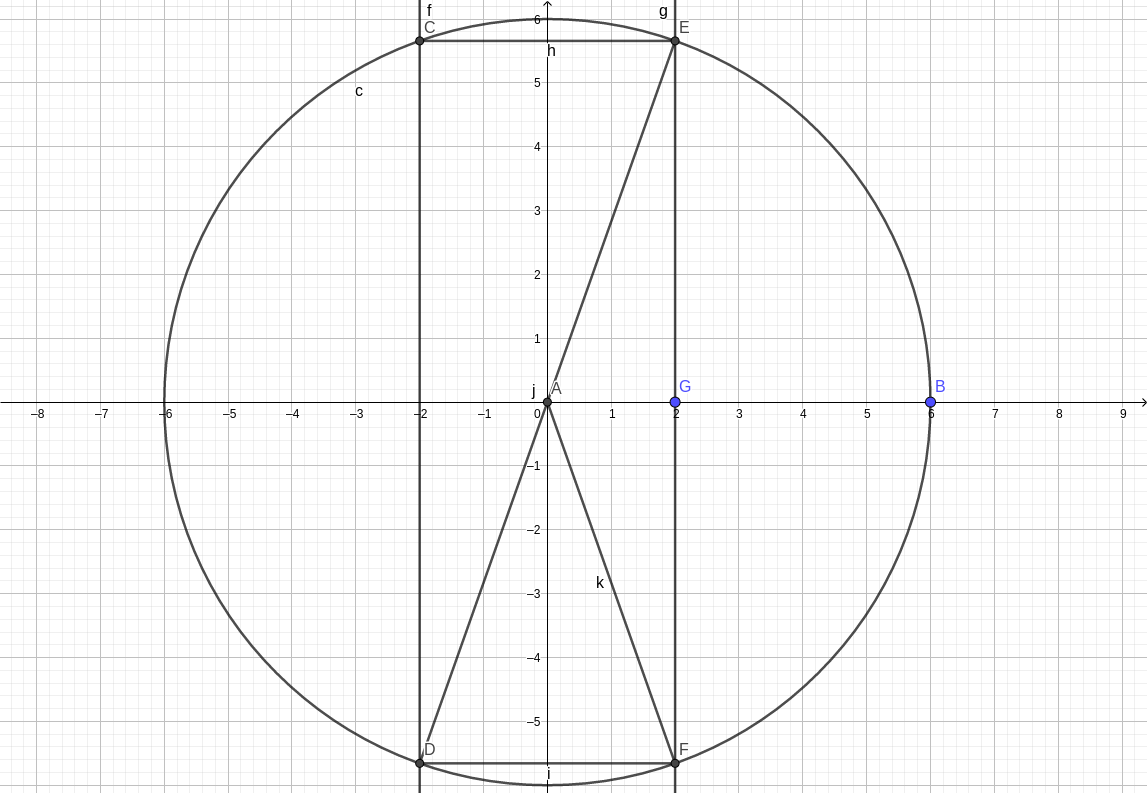
其中我们假设二维意义下这个硬币以圆的各个角度落下的概率一样,则只有落在(overset{frown}{CE})与(overset{frown}{DF})才会立起,依题意,这两段弧占整个圆周的(1over 3),即(∠DAF=60°),则(∠DEF=30°),(frac {EF}{DF}=sqrt 3)
但上面这种解法是错的,因为考虑三维意义下,因为三维意义下,硬币从三维空间内的任意一个方向都有可能,所以我们需要考虑球的情况。相应的,我们需要求球冠的面积,对应上面那副图,我们将其想象成球的一个截面,不能立起的情况就是落在两边的球冠内
我们考虑球冠面积等于球面积的(frac 23),即(2cdot 2pi rh=frac 23 cdot 4pi r^2),得(h=frac 23 r)
球冠的百度百科中还有明显的错误,已提出质疑,这个词条还是什么“专家评审”,这么简单的错误都看不出
则圆柱高的一半即(AG=frac 13r),(EG=frac {2sqrt 2}3r)
则硬币直径与厚度比为