题解-UOJ284 快乐游戏鸡

Problem

uoj

题意大意：

一棵树，点权(w_i)，每次玩家可以在树上行走，一条边需要(1)的时间，只能往儿子走。每次游戏需要从(s)到(t)。

玩家有一个总死亡次数，初始为(0)。如果走到(i)的时候，当前总的死亡次数小于(w_i)，那么玩家就会立刻死亡并回到起点 (s)，且该死亡过程不需要时间，多组询问从(s)到(t)的最短时间

(n,mleq 3 imes 10^5,w_ileq 10^9)

Solution

不难发现每次死亡都互相独立，所以对于每次死亡都单独计算

我们设(f[x][i])表示节点(x)往下走，已经死亡(i-1)次，死亡第(i)次所花费的最短时间，假如从(s)到(t)之间的最大点权为(W)，则答案为(sum_{i=1}^Wf[s][i]+dis(s,t))

解释一下，如果路径上最大点权为(W)，则从(s)到(t)的过程中一定恰好死(W)次（因为如果没死(W)次，则无法通过，一旦死亡(W)次，则接下来的点都可以通过且不会死亡），则答案记为(sum_{i=1}^Wf[s][i])，最后还要来一次从(s)到(t)的畅通无阻的旅行，答案加上(dis(s,t))

如何得到(f[x][i])？可以简单(Dp)，时间空间复杂度都为(O(nW))，我们可以拿到(10)分的好成绩，离散化一下可以多拿(10)分 (｡･∀･)ﾉﾞ

优化转移，发现(f[x][i])可能有一大段是相同的，而且(f[x][i])一定依照(i)严格递增，我们只需要记录转折点了

比如说对于(f[x][i])我们记录了(<f_1,f_4,f_{12},f_{40}>)，则对于(iin [5,12])，(f[x][i]=f_{12})

这样的话我们拿平衡树维护这个(<f_i>)，答案可以维护

答案转移可以平衡树启发式合并，具体就是所有子树相应位置取(min)，然后整体加(1)，询问完答案后，再将位置([1,w_i])之间的值赋为(0)

我：“好了，我们开始打吧”

（一个小时后）

我：“这太恶心了，浑身难受，不想继续，我们还是用正解的方法吧”

同桌：“这怎么行呢，代码再长，忍忍就过去了，而且你就是要培养这种调试的能力”

我：“好吧”（开始硬着头皮开始打）

（20分钟后）

同桌：“啊，我不打了，这太恶心了，我还没打完主程序就有300行了，我们还是看正解吧”

我：“不行不行，你要坚持，怎么能放弃呢，代码再长，忍忍就过去了，而且就是要培养这种调试的能力嘛”

同桌：“算了算了，我放弃了，我们还是用正解做法吧”

---

如上，我们发现用上述方法会导致浑身蓝瘦

所以我们有种奇妙的代码优化，就是

队列启发式合并

具体怎么做呢，就是整体开一个长队列，按照(dfs)序分配队列空间，这样合并一棵子树的时候由于(dfs)序是连续的，所以在队列中的空间也是连续的，这样合并起来的话，继续用合并起来的空间，这就显得很巧妙了

合并两个队列的时候将短的队列加入长的队列，而队列的长度上限取决于这个子树内的最长链，如果我们采用长链剖分，则每条长链只会被遍历一次，时间复杂度是(O(n))的，询问的时候二分查找第一个大于等于(W)的值，将前面的整体部分记上，再加上后面多出来的

如图，横坐标为(depth)，纵坐标为(w)，我们求的值就是下面的面积（其中队列里存的节点为染成蓝绿色的(A,C,E,G)）（感谢@zjp_shadow提醒弱智博主修复）

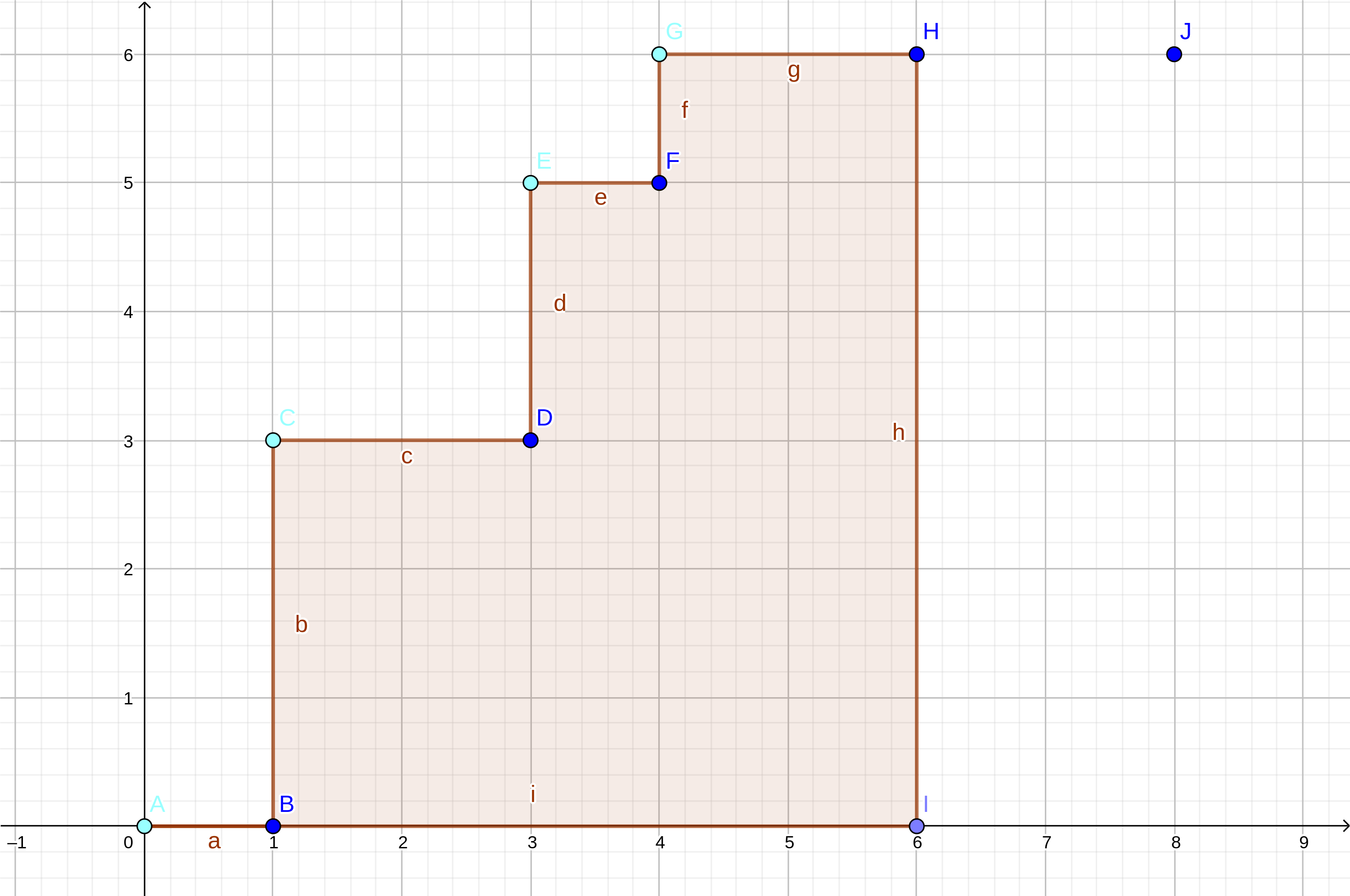
整体复杂度(O((n+m)log n))，具体做法详见代码

Code

#include <bits/stdc++.h>
typedef long long ll;

template <typename _tp> inline void read(_tp&x){
	char ch=getchar(),ob=0;x=0;
	while(ch!='-'&&!isdigit(ch))ch=getchar();if(ch=='-')ob=1,ch=getchar();
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();if(ob)x=-x;
}

template <typename _tp> inline void cmax(_tp&A,_tp B) {A = A > B ? A : B;}
template <typename _tp> inline _tp max(_tp A,_tp B) {return A > B ? A : B;}

const int N=301000;
struct Edge{int v,nxt;}a[N+N];
int head[N],Head[N],dep[N];
int he[N],ta[N],dfn[N],son[N];
int Q_t[N],w[N],n,m,dfc=1,_;

ll Ans[N],sm[N];

inline void add(int*arr,int u,int v){a[++_].v = v, a[_].nxt = arr[u], arr[u] = _;}

struct vLCA{
	int anc[N][20],ans_F[N][20],len[N];
	inline vLCA(){memset(len,0,sizeof len); len[0] = -1;}
	int query(int x,int y){
		int res(0);
		for(int i=19;~i;--i)
			if(dep[anc[x][i]] > dep[y])
				cmax(res,ans_F[x][i]), x = anc[x][i];
		return res;
	}
	void dfs(int x){
		for(int i=1;i<20;++i){
			anc[x][i] = anc[anc[x][i-1]][i-1];
			ans_F[x][i] = max(ans_F[x][i-1], ans_F[anc[x][i-1]][i-1]);
		}
		for(int i=head[x];i;i=a[i].nxt){
			anc[a[i].v][0] = x;
			ans_F[a[i].v][0] = w[x];
			dep[a[i].v] = dep[x] + 1;
			dfs(a[i].v);
			if(len[a[i].v] > len[son[x]])
				son[x] = a[i].v;
		}
		len[x] = len[son[x]] + 1;
	}
}lca;

struct node{
	int dep,w;
	inline node(){}
	inline node(const int&Dep,const int&W):dep(Dep),w(W){}
}p[N],tmp[N];

void ins(int x, node e) {
	while(he[x] <= ta[x] and p[he[x]].w <= e.w)++he[x];
	if(he[x] > ta[x] or p[he[x]].dep > e.dep){
		sm[he[x]-1] = 0;
		if(he[x] <= ta[x]) sm[he[x]-1] = (ll)(p[he[x]].w - e.w) * p[he[x]].dep + sm[he[x]];
		p[--he[x]] = e;
	}
}

void merge(int x,int y){
	int tp=0;
	while(he[x] <= ta[x] and p[he[x]].dep < p[ta[y]].dep)
		tmp[++tp] = p[he[x]++];
	while(tp and he[y] <= ta[y])
		if(p[ta[y]].dep > tmp[tp].dep) ins(x,p[ta[y]--]);
		else ins(x, tmp[tp--]);
	while(tp) ins(x, tmp[tp--]);
	while(he[y] <= ta[y]) ins(x,p[ta[y]--]);
}

void solve(int x,int id){
	int y = Q_t[id], op; ll res = 0ll;
	int l = he[x], r = ta[x], mid, w = lca.query(y,x);
	while(l<r){
		mid = l + r>> 1;
		if(p[mid].w < w) l = mid + 1;
		else r = mid;
	}
	op = bool(p[he[x]].w <= w);
	if(op) res = sm[he[x]] - sm[l] + (ll)p[he[x]].w * p[he[x]].dep;
	res += (ll)p[l].dep * (w-(op?p[l].w:0)) - (ll)dep[x]*w;
	Ans[id] = res + dep[y] - dep[x];
}

void dfs(int x){
	dfn[x] = ++dfc;
	if(son[x]) dfs(son[x]), he[x] = he[son[x]], ta[x] = ta[son[x]];
	else he[x] = dfc, ta[x] = dfc - 1;
	for(int i=head[x];i;i=a[i].nxt)
		if(a[i].v != son[x])
			dfs(a[i].v), merge(x,a[i].v);
	for(int i=Head[x];i;i=a[i].nxt)
		solve(x,a[i].v);
	ins(x,node(dep[x],w[x]));
}

void input();
void print();
int main(){
	input(); lca.dfs(1);
	dfs(1); print();
	return 0;
}

void print(){
	for(int i=1;i<=m;++i)
		printf("%lld
",Ans[i]);
}

void input(){
	read(n), dep[1] = 1; int x;
	for(int i=1;i<=n;++i) read(w[i]);
	for(int i=2;i<=n;++i) read(x), add(head,x,i);
	read(m);
	for(int i=1;i<=m;++i){
		read(x), read(Q_t[i]);
		add(Head,x,i);
	}
}