1.SLAM问题
1.1建模
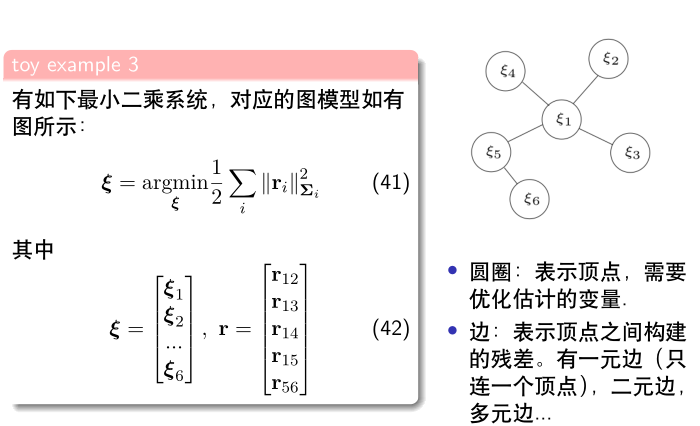
考虑某个状态 (xi),以及一次与该变量相关的观测 (r_{i})。由于噪声存在,观测服从概率分布 (p(r_{i}|xi))。多个观测时,各个测量值相互独立,则多个测量 (r = (r_{1}, ..., r_{n})^{T})构成的似然概率为: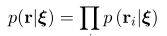
如果知道机器人状态的先验信息 (p(xi)),如GPS,码盘信息等,则由贝叶斯法则,有后验概率:
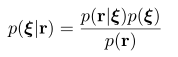
通过最大后验估计,获得系统状态的最优估计:
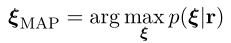
意为在当前的观测下,什么样的系统状态出现的概率最大。
分母跟状态量无关,舍弃取log。即:
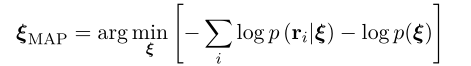
如果观测服从多元高斯分布:
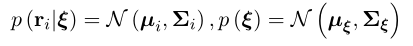
则有:
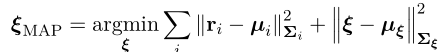
该问题可由最小二乘求解:
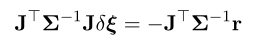
零均值的多元高斯分布概率为:(p(x) = frac{1}{Z}exp(-frac{1}{2}x^{T}Sigma^{-1}x))
其中(Sigma)是协方差矩阵。(Sigma^{-1})为协方差矩阵的逆,即信息矩阵。
2.边缘化信息矩阵
使用滑动窗口不可避免的要移除掉变量,当移除变量的时候,之前与之不相关的变量,有可能变得相关,所以要对信息矩阵进行维护。
这里使用舒尔补来对信息矩阵进行边缘化处理。
2.1舒尔补的定义:
给定任意的矩阵块M,如下所示:
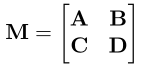
如果,矩阵块D是可逆的,则 (A-BD^{-1}C)称之为D关于M的舒尔补
如果。矩阵块A是可你的,则 (D-CA^{-1}B)称之为A关于M的舒尔补
2.2使用舒尔补来去除变量:
假如一个系统三个变量x1,x2,x3。其信息矩阵为:
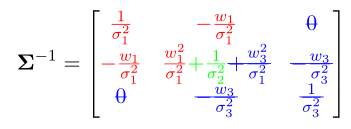
那么把x3去掉,也就是把蓝色部分去掉,利用舒尔补。
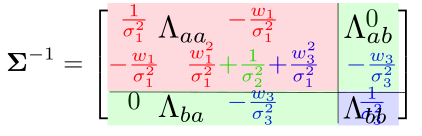
则去掉后的信息矩阵为:
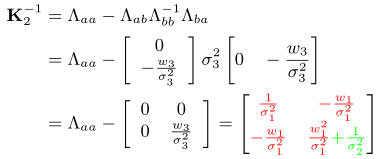
3.滑动窗口算法
上述最小二乘问题,对应的高斯牛顿求解为:

注意:这里的H反应的是求解的方差,而(Sigma^{-1})反应的是残差的方差
公式中的雅可比矩阵为:
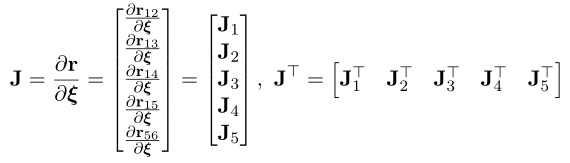
矩阵乘法公式可以写成连加:
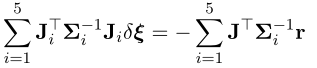

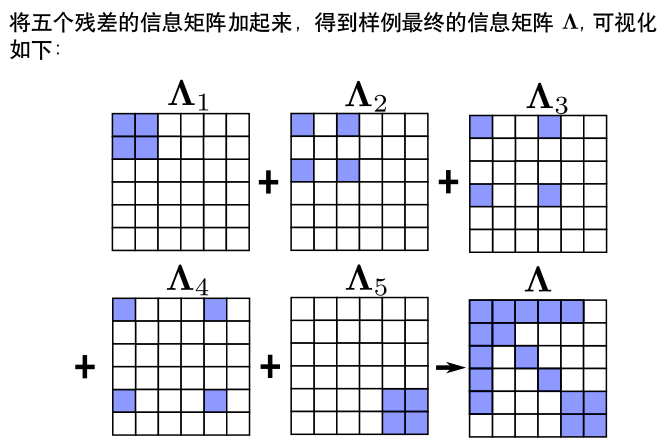
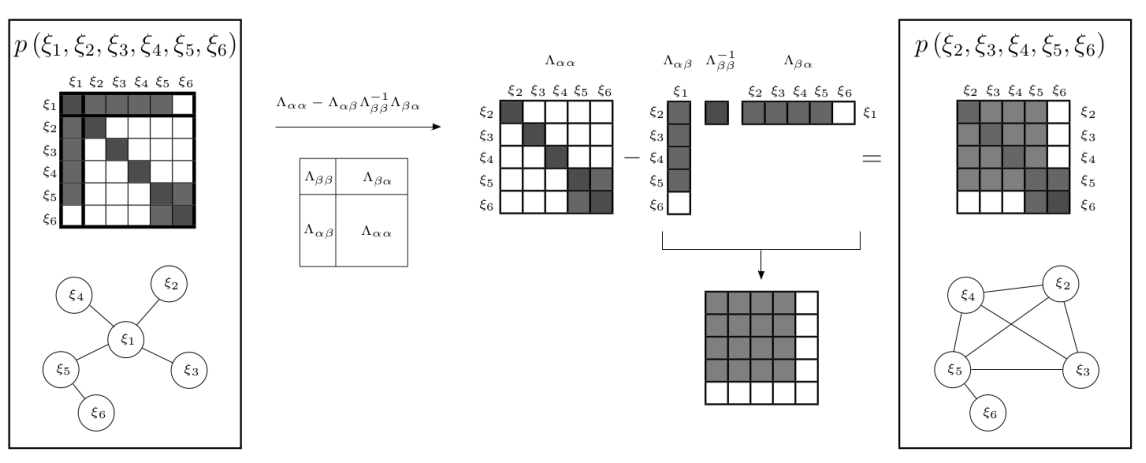
使用边际概率移除变量(xi_{1}),信息矩阵的变化过程: