【问题背景】
今天是一个阳光明媚,风和日丽的好日子,猪爸爸和猪妈妈带着佩奇和乔治去海滩玩耍。佩奇突发奇想,给乔治出了这么一道题。
【问题描述】
栈是常用的一种数据结构,有n个元素在栈顶端一侧等待进栈,栈顶端另一侧是出栈序列。你已经知道栈的操作有两种:push和pop,前者是将一个元素进栈,后者是将栈顶元素弹出。现在要使用这两种操作,由一个操作序列可以得到一系列的输出序列。请你编程求出对于给定的n,计算并输出由操作数序列1,2,…,n,经过一系列操作可能得到的输出序列总数。
乔治才两岁,没法解决这么难的问题。这时,你恰好从乔治身边经过,于是他向你求助,请你帮助他解决这个问题。
【输入】【输出】
就一个数n(1≤n≤1000)。 一个数,即可能输出序列的总数目。
【样例】
stack.in stack.out
3 5
【胡乱分析】
设a,b,c分别代表等待进栈元素个数,栈中元素个数,出栈元素个数。元素的总个数n=a+b+c。则c=n-a-b,所以,只要知道a和b的数值,就可以求出c。那么对于这些元素来说,存在以下操作:①既进栈又出栈②只进栈不出栈③只出栈不进栈,那么对于三种操作,等待进栈元素个数与栈中元素个数也会进行相应的变化。
.用f(a,b)表示从(a,b)变为(0,0)的所有移动方法。即f(n,0)。写出以下递归式
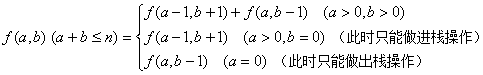
边界值:f(0,0)=1。
对于原题,起初有n个元素等待进栈,栈中有0个元素。即f(n,0)
代码如下:
1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #include<cmath> 5 #include<cstring> 6 using namespace std; 7 int n; 8 int f(int a,int b) 9 { 10 if(a == 0 && b == 0) 11 return 1; 12 else if(a > 0 && b > 0) 13 return f(a-1,b+1)+f(a,b-1); 14 else if(a > 0 && b == 0) 15 return f(a-1,b+1); 16 else if(a == 0) 17 return f(a,b-1); 18 } 19 int main() 20 { 21 scanf("%d",&n); 22 printf("%d",f(n,0)); 23 return 0; 24 }
end。