这是一道模板题
这里是题目 洛谷P3807
卢卡斯定理及题目的阐释
卢卡斯定理是用来解决一大很大的组合数来和一个质数求余的问题,它的定义如下
如果p为素数,设n=sp+q,m=tp+r
则:
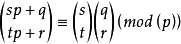
那么来看看题。
首先看这个数据范围,就知道可以用int的类型解决个屁,就是int害的我错了好多次long long 的数据类型解决,这个数据看起来好像是只有 10的5次方,但是中间这么多的计算,突然的就给我溢出了我靠着ZFN大佬的数据测试发现负数才发现的。
long long C(int n,int m,int p){
if(n<m)return 0;
if(n==m)return 1;
if(m>n-m)m=n-m;//约掉
long long s1=1,s2=1;
for(int i=0;i<m;i++){
s1=s1*(n-i)%p;
s2=s2*(i+1)%p;
}
return s1*qkpow(s2,p-2,p)%p;
}
这一段是求组合的函数,拿出来单独讲一讲
因为这里面的参数传过来的时候都是已经和p求过余了的,而且p在题目中说了的,是一个质数所以说这里的n,m都是和p互质的。
因为公式里面要除掉m!,同时有要去对p取模,所以考虑用它的逆元乘来代替用它来除
而根据费马小定理可以知道它的逆元是它的p-2方
代码
那么综上,加上以个快速幂就可以解出这道题了
//洛谷P3807 Lucas 模板题
#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m,p;
long long qkpow(long long b,int p,int mod){
long long res=1;
while(p){
if(p&1){
(res*=b)%=mod;
}
(b*=b)%=mod;
p>>=1;
}
return res;
}
long long C(int n,int m,int p){
if(n<m)return 0;
if(n==m)return 1;
if(m>n-m)m=n-m;//约掉
long long s1=1,s2=1;
for(int i=0;i<m;i++){
s1=s1*(n-i)%p;
s2=s2*(i+1)%p;
}
return s1*qkpow(s2,p-2,p)%p;
}
long long Lucas(int n,int m,int p){
if(m==0)return 1;
return C(n%p,m%p,p)*Lucas(n/p,m/p,p)%p;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
#endif
int t;
scanf("%d",&t);
while(t--){
scanf("%d%d%d",&n,&m,&p);
n+=m;
cout<<Lucas(n,m,p)<<"
";
}
return 0;
}