20180414模拟赛T2——拼图

拼图

• 源程序名 　 puzzling.??? (PAS,BAS,C,CPP)
• 可执行文件名 puzzling.EXE
• 输入文件名　　 puzzling.IN
• 输出文件名 puzzling.OUT
• 时间限制 1S
• 内存限制 128MB

背景

潘帕斯草原最近流行起了一种拼图游戏，@潘帕斯雄鹰为了显示自己是最强的鹰，想尽办法要在这个游戏上赢过其他鹰……

题目描述

这个拼图游戏要求将一些图形拼成一个正方形，图形的个数从1到5。如下图所示，图形个数是4。

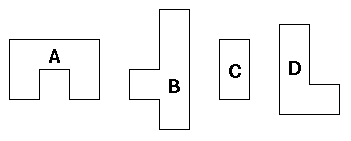
图形不能旋转，拼的时候不能重叠，拼完后的正方形里面不能有空隙。所有给定的图形都要使用。

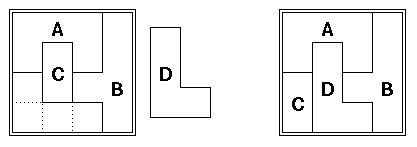
左面的图表示这样拼不行，右面是一个成功的拼法。

现在，@潘帕斯雄鹰想知道他能否完成这个游戏以表示自己是最强的鹰；如果可以，请输出一种完成这个游戏的方案。

输入格式：

文件的第一行是一个整数n，表示图形的个数，范围从1到5。
接下来有n个部分，每个部分的第一行是2个整数i和j，表示下面的i行j列用来描述一个图形。图形用0和1表示，1表示图形占有这个位置，0表示不占有，中间没有空格。例如上图中图形A的描述是

2 3
111
101

所有图形的长与宽都不超过5。
根据图形给出的顺序给每个图形编号，从1开始，至多到5。
保证数据无多解情况。

输出文件：

如果不能拼成一个正方形，就输出“No solution possible”；否则，输出一种拼的方案：一个正方形的数阵，每个位置上的数字是占有这个位置的图形的编号，中间没有空格。例如上面A、B、C、D的编号依次是1、2、3、4，那么就可以输出

1112
1412
3422
3442

输入样例1：

4
1 4
1111
1 4
1111
1 4
1111
2 3
111
001

输出样例1：

No solution possible

输入样例2：

5
2 2
11
11
2 3
111
100
3 2
11
01
01
1 3
111
1 1
1

输出样例2：

1133
1153
2223
2444

题解

这题数据范围小，于是显然是深搜（dfs大法好）。

对了，得吐槽一下测试点1,2的数据：

puzzling.in

1
4 4
0000
0010
0000
0000

puzzling.ans

1

测试点2也差不多。

于是判边界的全炸了。

觉得这题主要考的是代码实现能力，就直接贴代码吧：

#include <cstdio>
#include <cstdlib>
#include <cstring>

using namespace std;

#define re register

int n,k,ans,a[10],b[10],s[10][10],xx[10],yy[10],f[10];
char c[10][10][10];
bool fk,flag[10];//flag[i]:i是否用过 

inline int sqrt(int x)//c++自带sqrt可能会有精度问题，于是索性手打 
{
	for(register int i=0; i<=x; ++i)//反正x很小，枚举即可 
	{
		int t=i*i;
		if(t==x)return i;
		if(t>x)return -1;
	}
	return -1;
}

inline void doit()//判断是否填成了一个正方形 
{
	int x=1,y=1,x1,y1;
	memset(s,0,sizeof(s));
	for(re int l=1;l<=n;++l)
	{
		for(;s[x][y];)
		{
			++y;if(y>k)y=1,++x;
		}
		x1=x-xx[f[l]];y1=y-yy[f[l]];
		for(re int i=1;i<=a[f[l]];++i)
			for(re int j=1;j<=b[f[l]];++j)
				if(c[f[l]][i][j]=='1')
				{
					if(i+x1>k||j+y1>k||i+x1<=0||j+y1<=0)return;
					if(!s[i+x1][j+y1])s[i+x1][j+y1]=f[l];
					else return;
				}
	}
	for(re int i=1;i<=k;++i,puts(""))
		for(re int j=1;j<=k;++j)
			printf("%d",s[i][j]);
	exit(0);//直接退出程序 
}

inline void dfs(int k)//愉快的dfs时间
{
	if(k==n){doit();return;}
	for(re int i=1;i<=n;++i)
		if(!flag[i])
		{
			flag[i]=true;f[k+1]=i;
			dfs(k+1);flag[i]=false;
		}
}

int main()
{
	freopen("puzzling.in","r",stdin);
	freopen("puzzling.out","w",stdout);
	scanf("%d",&n);
	for(re int i=1;i<=n;++i)
	{
		scanf("%d%d
",&a[i],&b[i]);
		fk=false;
		for(re int j=1;j<=a[i];++j)
		{
			for(int k=1;k<=b[i];++k)
			{
				c[i][j][k]=getchar();
				if(c[i][j][k]=='1')ans++;
				if(c[i][j][k]=='1'&&!fk){xx[i]=j;yy[i]=k;fk=true;}
			}
			getchar();//注意有'
' 
		}
	}
	k=sqrt(ans);
	if(k==-1)return puts("No solution possible"),0;
	dfs(0);
	return puts("No solution possible"),0;
}