Summary
今天比赛很差很差,掉到谷底。第一题快排打错了,漏了递归,变成一个while循环。最后一题k忘记减一,答案一直是无穷大,所以没交。第三题没时间调DP就打了个递归,第二题状态想歪了。四道题有三道DP的,一道小码力的。DP可见很差,还要多学,多做。快排打到一半傻乎乎就没打了,样例数据又刚好都是对的,不会对拍。马上就要学一下啊!
Problem
T1 平台
题目大意
给你一堆平台,每个平台平行于x轴,距离x轴有个高度h。每个平台由两个柱子支撑,分别在离端点0.5个单位的位置。问柱子的长度和
想法
鉴于平台个数很小,平台的横坐标小,直接暴力即可。
先将平台高度从小到大排序,然后用bz数组,bz[i]表示横坐标为i时,上面最高的平台高度是多少,每次查找就行了。
因为有0.5这种小数的情况,所以可以将所有坐标乘以二。
T2 单足跳
题目大意
游戏在一行N个方块中进行,编号为1到N,一开始Alice在方块1中,第一次只能跳到方块2中,接下来每一次跳跃必须满足以下两个限制:
(1) 如果是向前跳(即跳到比现在编号大的方块),跳跃距离必须比上一次要大1;
(2) 如果是向后跳(即跳到比现在编号小的方块),跳跃距离必须跟上一次一样。
每个方块有个花费值,问从方块1到方块n的最小花费值。
想法
考试的时候我是这么设的
f[i,j]表示第i次到j这个位置的最小花费值,怎么转移都不对。大家也可以想一下,评论一下。
正解是这样的
设f[i,j]表示你花费i步走到j这个位置。
显然,我们两种方案,一种往前,一种往后
往前的情况:
我们会到达j-i这个位置,根据题目意思,同样是花费i步过去,所以这么转移f[i,j-i]=min{f[i,j-i],f[i,j]+a[j-i]}
当然,j一定符合范围
往后的情况:
我们会往后跳i+1位,即到达j+i+1这个位置,他是花费i+1步过去,故转移为f[i+1,j+i+1]=min{f[i+1,j+i+1,f[i,j]+a[j+i+1]}
题目很快就解决完毕了。
T3 生日聚餐
题目大意
晚餐由N种原料做成,每道菜所需每种原料的数量是一样的。
厨房里有一些原料,但不够,Alice还需要从旁边的超市中购买一些回来。超市里什么原料都有,每种原料都分大包装和小包装。Alice有M元钱,她想利用这M元钱购买原料使得能做出最多的菜。
想法
跟之前做过的一道题差不多,同样可以先求完全背包,然后枚举答案,二分答案也是可以的。
我们用f[i,j]表示第i种材料,用了j数量的最小价值
我们求完后需要维护一下f数组,因为可能刚好不能组成j数量的物品,但是用多点钱还是可以买到。例如你5块钱可以买到6块橡皮擦,但是你只需要5块,商店又不能分开买,你买5块橡皮擦,同样也是需要5块钱。
然后我们枚举(二分)答案,也就是做多少钱数,我们设这个数为i。
答案就是
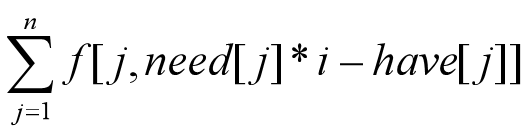
显然这个是递增的,取个最大符合条件的值,对应的i就是答案
这就是二分求解的东西,故可以用二分
f数组的空间会炸,所以可以使用动态数组(可以在程序中根据需要定义数组大小)
下面是一维的定义方式(pascal),二维的只需要加多括号内容
var
a:array of (array of) longint;
begin
setlength(a,s,(s1))表示第一维下标开0~s-1大小,括号中,第二维表示下标开从0~s1-1大小
end.
T4 数学题
题目大意
给你一串数,让他们可以往里面加加号,使之等于一个数,问最少的加加号个数。
想法
我们可以想到动态规划。
设f[i,j]表示选到前i个数,和为j所加的最少加号个数是多少。
我们枚举i,j,k,如图标明位置
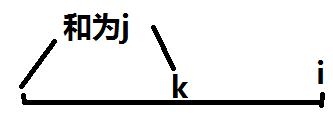
其中,我们要把k~i这些数弄成一个数,独立起来,也就是说,在k前面放一个加号。
显然,转移就是f[i,j+ans]=min{f[i,j+ans],f[k,j]},Ans就是k~i这些数组合成一个的那个新的数。
还有一种情况就不放加号
f[i,j*10+a[i]]=min{f[i,j*10+a[i]],f[i-1,j])。很显然,你这么做最多加4次,你就会被挂了,因为一直不放加号,数的大小可想而知。
到目前为止,时间复杂度是O(n³),显然你会炸的巴拉巴拉的
唯一可能优化的就是k,其实k枚举这么多是不必要的,关键还是0的问题
所以,我们对输入的字符串处理一下,最多只能有4个连续的0
时间复杂度:O(4n²)