Link
https://jzoj.net/senior/#main/show/1417
Problem
当Alice在浏览数学书时,看到一个等式A=S,奇怪的是A和S并不相等。Alice发现可以通过在A中添加加号“+”从而使得等式成立。
编程计算最少需要插入多少加号使得等式成立。允许每个数有多个前导0。
Solution
20分
暴力乱搞
100分
我们可以想到动态规划。
设f[i,j]表示选到前i个数,和为j所加的最少加号个数是多少。
我们枚举i,j,k,如图标明位置
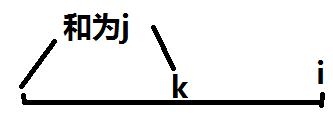
其中,我们要把k~i这些数弄成一个数,独立起来,也就是说,在k前面放一个加号。
显然,转移就是f[i,j+ans]=min{f[i,j+ans],f[k,j]},Ans就是k~i这些数组合成一个的那个新的数。
还有一种情况就不放加号
f[i,j*10+a[i]]=min{f[i,j*10+a[i]],f[i-1,j])。很显然,你这么做最多加4次,你就会被挂了,因为一直不放加号,数的大小可想而知。
到目前为止,时间复杂度是O(n³),显然你会炸的巴拉巴拉的
唯一可能优化的就是k,其实k枚举这么多是不必要的,关键还是0的问题
所以,我们对输入的字符串处理一下,最多只能有4个连续的0
时间复杂度:O(4n²)