[jzoj]3875.【NOIP2014八校联考第4场第2试10.20】星球联盟(alliance)

Link

　　https://jzoj.net/senior/#main/show/3875

Problem

　　在遥远的S星系中一共有N个星球，编号为1…N。其中的一些星球决定组成联盟，以方便相互间的交流。
　　但是，组成联盟的首要条件就是交通条件。初始时，在这N个星球间有M条太空隧道。每条太空隧道连接两个星球，使得它们能够相互到达。若两个星球属于同一个联盟，则必须存在一条环形线路经过这两个星球，即两个星球间存在两条没有公共隧道的路径。
　　为了壮大联盟的队伍，这些星球将建设P条新的太空隧道。这P条新隧道将按顺序依次建成。一条新轨道建成后，可能会使一些星球属于同一个联盟。你的任务是计算出，在一条新隧道建设完毕后，判断这条新轨道连接的两个星球是否属于同一个联盟，如果属于同一个联盟就计算出这个联盟中有多少个星球。

Solution

　　题目太长也太烦，幼稚而又没智商。

　　题目大意是：“给你n个点，m条边，给出p个询问，每个询问给出一条边，先连这条边，然后判断两个点是否处在环内，是的话就输出环的大小”

　　我们考虑使用一种方便计算答案的连边方式

　　对于输入的m+p条边，我们每次连的边，要符合以下条件才连

　　连了这条边，不会让图中有环。

　　为什么这样连是对的呢？因为连了对答案没有任何贡献。

　　怎么判环呢？用并查集判断两点祖先是否相同，并给祖先之间连一条边。

　　根据这个判定条件连完边，整个图，就是一个森林（很多树）。

　　在之后的判断里，如果这条边在有判定条件的那次连边中连过了，那说明他怎么连都不会构成环，所以输出No。

　　然后，再对之前没有连的边处理。我们设当前没有连的边为x~y

　　那么，连了这个边一定会构成一个环，这个环的大小，其实就是求x~lca(x,y)+y~lca(x,y)的长度，可以看下面的图。（红色代表边x~y，其中，黑色圈圈住的部分即环的大小）

　　　

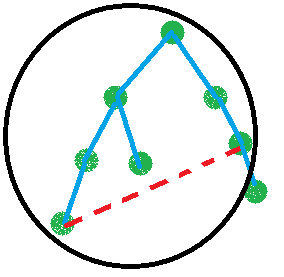
　　找出了答案后，我们进行缩点处理。

　　因为这环中每一个点的答案，都是一样的，所以，我们可以把答案存在lca这个点上，在之后的询问中，如果遇到这个环中的点，就跳到lca的地方去。这个操作，同样用并查集操作。把环中的点，他们的father，直接赋值为lca。但是，不是将他们的祖先赋值为lca的祖先上去。

　　每次我们找到一个点，我们直接跳到他f数组中的父亲上，以免重复计算同一个环上的数值。

　　如果一个在执行操作时，一个环中套一个环，那么先形成的环，他的父亲通过并查集，一定赋值为后形成的环的父亲，故只计算一次。

　　大概流程：每次模拟找lca，然后跳到当前点并查集中的父亲上，知道跳到他们的lca，计算答案。

Code

　　打得很臭，也很丑，见谅

{$inline on}
var
        n,m,p,i,j,x,y,xx,yy,tot,ans,lca:longint;
        bz:array[0..400000] of boolean;
        a:array[0..400000,0..2] of longint;
        l,pre,d:array[0..800000] of longint;
        f,re,dad,dis,shen,have:array[0..200000] of longint;
procedure insert(x,y:longint); inline;
begin
        inc(tot);
        d[tot]:=y;
        pre[tot]:=l[x];
        l[x]:=tot;
end;

function getfather(x:longint):longint; inline;
begin
        if f[x]=0 then exit(x);
        f[x]:=getfather(f[x]);
        exit(f[x]);
end;

procedure he(x,y:longint);   inline;
var
        fx,fy:longint;
begin
        fx:=getfather(x);
        fy:=getfather(y);

        if fx<>fy then
                f[fx]:=fy;

end;

procedure build(x,num,q:longint); inline;
var
        k:longint;
begin
        dad[x]:=q;
        shen[x]:=num;

        k:=l[x];
        while k<>0 do
        begin
                if dis[d[k]]=0 then
                begin
                        dis[d[k]]:=1;

                        build(d[k],num+1,x);
                end;

                k:=pre[k];
        end;
end;

procedure check(var x,y:longint);   inline;
begin
        while shen[x]<>shen[y] do
        begin
                while shen[x]>shen[y] do
                begin
                        ans:=ans+re[x];

                        inc(have[0]);
                        have[have[0]]:=x;

                        x:=dad[x];

                        x:=getfather(x);
                end;

                while shen[x]<shen[y] do
                begin
                        ans:=ans+re[y];

                        inc(have[0]);
                        have[have[0]]:=y;

                        y:=dad[y];

                        y:=getfather(y);
                end;
        end;
end;

begin
        readln(n,m,p);

        for i:=1 to m+p do
        begin
                readln(x,y);

                if getfather(x)<>getfather(y) then
                begin
                        he(x,y);

                        insert(x,y);
                        insert(y,x);

                        bz[i]:=true;
                end;

                a[i,1]:=x;
                a[i,2]:=y;
        end;

        for i:=1 to n do
                if dis[i]=0 then
                begin
                        dis[i]:=1;

                        build(i,1,i);
                end;

        fillchar(f,sizeof(f),0);

        for i:=1 to n do
                re[i]:=1;

        for i:=1 to m do
        begin
                if bz[i] then
                        continue;

                x:=getfather(a[i,1]);
                y:=getfather(a[i,2]);

                ans:=0;
                have[0]:=0;

                check(x,y);

                while x<>y do
                begin
                        ans:=ans+re[x]+re[y];

                        inc(have[0]);
                        have[have[0]]:=x;
                        inc(have[0]);
                        have[have[0]]:=y;

                        x:=dad[x];
                        y:=dad[y];

                        x:=getfather(x);
                        y:=getfather(y);

                        check(x,y);
                end;

                ans:=ans+re[x];

                re[x]:=ans;

                for j:=1 to have[0] do
                begin
                        f[have[j]]:=x;

                        re[have[j]]:=ans;
                end;
        end;
        /////////////////////////////////////////////////////////////

        for i:=m+1 to m+p do
        begin
                if bz[i] then
                begin
                        writeln('No');

                        continue;
                end;

                x:=getfather(a[i,1]);
                y:=getfather(a[i,2]);

                ans:=0;
                have[0]:=0;

                check(x,y);

                while x<>y do
                begin
                        ans:=ans+re[x]+re[y];

                        inc(have[0]);
                        have[have[0]]:=x;
                        inc(have[0]);
                        have[have[0]]:=y;

                        x:=dad[x];
                        y:=dad[y];

                        x:=getfather(x);
                        y:=getfather(y);

                        check(x,y);
                end;

                ans:=ans+re[x];

                re[x]:=ans;

                writeln(ans);

                for j:=1 to have[0] do
                begin
                        f[have[j]]:=x;

                        re[have[j]]:=ans;
                end;
        end;
end.