[jzoj]2505.【NOIP2011模拟7.29】藤原妹红

Link

　　https://jzoj.net/senior/#main/show/2505

Description

　　在幻想乡，藤原妹红是拥有不老不死能力的人类。虽然不喜欢与人们交流，妹红仍然保护着误入迷途竹林村民。由于妹红算得上是幻想乡最强的人类，对于她而言，迷途竹林的单向道路亦可以逆行。在妹红眼中，迷途竹林可以视为一个由N 个路口(编号1..N)，M 条不同长度双向路连接的区域。妹红所在的红之自警队为了方便在迷途竹林中行动，绘制了一张特殊的迷途竹林地图，这张地图上只保留了N-1 条道路，这些道路保证了任意两个路口间有且仅有一条路径，并且满足所有保留的道路长度之和最小，我们称这些道路为『自警队道路』。现在妹红打算在其中一个连接有多条『自警队道路』的路口设立根据地，当去掉这个根据地所在路口后，就会出现某些路口间无法通过『自警队道路』相互连通的情况，我们认为这时仍然能够通过『自警队道路』连通的路口属于同一个『区域』。妹红希望最后每个『区域』的『自警队道路』总长尽可能平均，请计算出她应该选择哪一个路口作为根据地。

　　(尽可能平均即权值最小，设每一块『区域』的路线总长为Length[i]，平均路线长度为Avg=SUM{Length[i]}/区域数，权值d=Σ((Length[i]-Avg)^2))

　　下例中红色的路口为妹红选择的根据地，实线边表示『自警队道路』，绿色虚线边表示非『自警队道路』，数字表示边权，『自警队道路』中相同颜色的实线边代表属于同一个『区域』：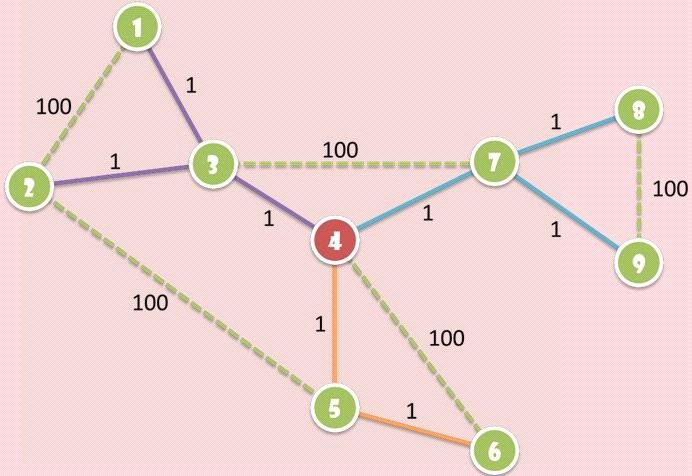

Solution

　　显然，我们可以跑一次最小生成树确定选哪n-1条边。

　　对搞出来的这片森林，每棵树跑一次dfs，确定根，找这棵树上的节点他们的父亲和其深度，并且记录一下x的儿子们中的边的和。

　　然后我们枚举每一个点，以他们为根。显然，它的贡献（大概说说，不对应题目的计算方法，大概是这样的）为他每个儿子的边长总和，他到每个儿子边长总和，以及比他深度更小的节点联通的边的边长总和。

　　这个画个图就可以理解了，挺简单的。

Code

{$inline on}
var
        min,sum,papa:real;
        n,m,i,j,x,y,tot,tott,minn:longint;
        a:array[0..400000,0..3] of real;
        dd,data:array[0..400000] of real;
        f,d,l,pre,ru,shen:array[0..400000] of longint;
procedure insert(x,y:longint;z:real); inline;
begin
        inc(tot);
        d[tot]:=y;
        dd[tot]:=z;
        pre[tot]:=l[x];
        l[x]:=tot;
        inc(ru[y]);
end;
procedure q(l,r:longint);  inline;
var
        t,mid:real;
        i,j:longint;
begin
        i:=l;
        j:=r;
        mid:=a[(l+r) shr 1,3];
        while i<j do
        begin
                while a[i,3]<mid do inc(i);
                while a[j,3]>mid do dec(j);

                if i<=j then
                begin
                        a[0]:=a[i]; a[i]:=a[j]; a[j]:=a[0];

                        inc(i); dec(j);
                end;
        end;

        if i<r then q(i,r);
        if l<j then q(l,j);
end;

function getfather(x:longint):longint;  inline;
begin
        if f[x]=0 then exit(x);
        f[x]:=getfather(f[x]);
        exit(f[x]);
end;

procedure he(x,y:longint);   inline;
var
        fx,fy:longint;
begin
        fx:=getfather(x);
        fy:=getfather(y);

        if fx<>fy then
                f[fx]:=fy;

end;

procedure search(now,q,du:longint);  inline;
var
        k:longint;
begin
        shen[now]:=du;
        k:=l[now];

        while k<>0 do
        begin
                if d[k]<>q then
                begin
                        search(d[k],now,du+1);

                        data[now]:=data[now]+data[d[k]]+dd[k];
                end;

                k:=pre[k];
        end;
end;

function check(now:longint):real;  inline;
var
        k,quyushu:longint;
        avg,ans,ttt:real;
begin
        if ru[now]<2 then
                exit(sum*sum);

        k:=l[now];

        ans:=0;
        ttt:=0;
        quyushu:=0;

        while k<>0 do
        begin
                inc(quyushu);
                k:=pre[k];
        end;

        avg:=sum/quyushu;

        k:=l[now];

        while k<>0 do
        begin
                if shen[d[k]]>shen[now] then
                begin
                        ans:=ans+sqr(data[d[k]]+dd[k]-avg);
                        ttt:=ttt+data[d[k]]+dd[k];
                end;

                k:=pre[k];
        end;

        ttt:=sum-ttt;

        ans:=ans+sqr(ttt-avg);

        exit(ans);
end;
begin
        readln(n,m);
        for i:=1 to m do
                readln(a[i,1],a[i,2],a[i,3]);

        q(1,m);

        for i:=1 to m do
        begin
                x:=trunc(a[i,1]);
                y:=trunc(a[i,2]);
                if getfather(x)<>getfather(y) then
                begin
                        he(x,y);

                        insert(x,y,a[i,3]);
                        insert(y,x,a[i,3]);

                        sum:=sum+a[i,3];
                end;
        end;

        search(1,1,1);

        min:=sum*sum;

        for i:=1 to n do
        begin
                papa:=check(i);
                if papa<min then
                begin
                        min:=papa;

                        minn:=i;
                end;
        end;

        writeln(minn);
end.