过去几年发表于各大 AI 顶会论文提出的 400 多种算法中,公开算法代码的仅占 6%,其中三分之一的论文作者分享了测试数据,约 54% 的分享包含“伪代码”。这是今年 AAAI 会议上一个严峻的报告。 人工智能这个蓬勃发展的领域正面临着实验重现的危机,就像实验重现问题过去十年来一直困扰着心理学、医学以及其他领域一样。最根本的问题是研究人员通常不共享他们的源代码。
可验证的知识是科学的基础,它事关理解。随着人工智能领域的发展,打破不可复现性将是必要的。为此,PaperWeekly 联手百度 PaddlePaddle 共同发起了本次论文有奖复现,我们希望和来自学界、工业界的研究者一起接力,为 AI 行业带来良性循环。
作者丨黄涛
学校丨中山大学数学学院18级本科生
研究方向丨图像识别、VQA、生成模型和自编码器

论文复现代码:
http://aistudio.baidu.com/#/projectdetail/23600
GAN
生成对抗网络(Generative Adversarial Nets)是一类新兴的生成模型,由两部分组成:一部分是判别模型(discriminator)D(·),用来判别输入数据是真实数据还是生成出来的数据;另一部分是是生成模型(generator)G(·),由输入的噪声生成目标数据。GAN 的优化问题可以表示为:
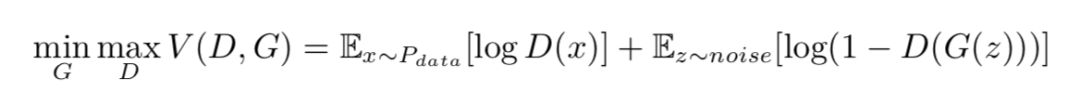
其中 Pdata 是生成样本,noise 是随机噪声。而对于带标签的数据,通常用潜码(latent code)c 来表示这一标签,作为生成模型的一个输入,这样我们有:
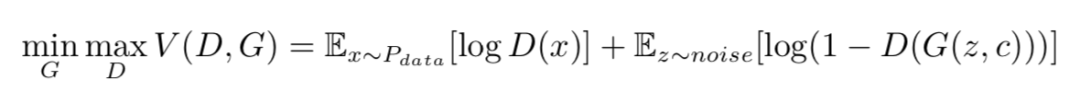
然而当我们遇到存在潜在的类别差别而没有标签数据,要使 GAN 能够在这类数据上拥有更好表现,我们就需要一类能够无监督地辨别出这类潜在标签的数据,InfoGAN 就给出了一个较好的解决方案。
互信息(Mutual Information)
互信息是两个随机变量依赖程度的量度,可以表示为:
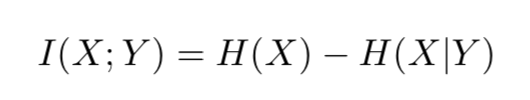
要去直接优化 I(c;G(z,c)) 是极其困难的,因为这意味着我们要能够计算后验概率(posterior probability)P(c|x),但是我们可以用一个辅助分布(auxiliary distribution)Q(c|x),来近似这一后验概率。这样我们能够给出互信息的一个下界(lower bounding):
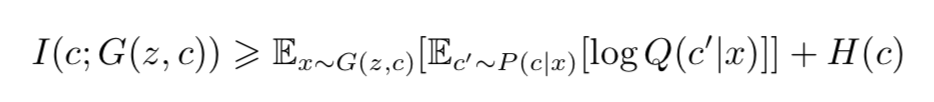
InfoGAN
在 InfoGAN 中,为了能够增加潜码和生成数据间的依赖程度,我们可以增大潜码和生成数据间的互信息,使生成数据变得与潜码更相关:
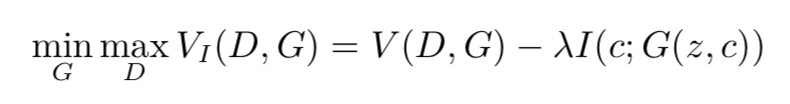
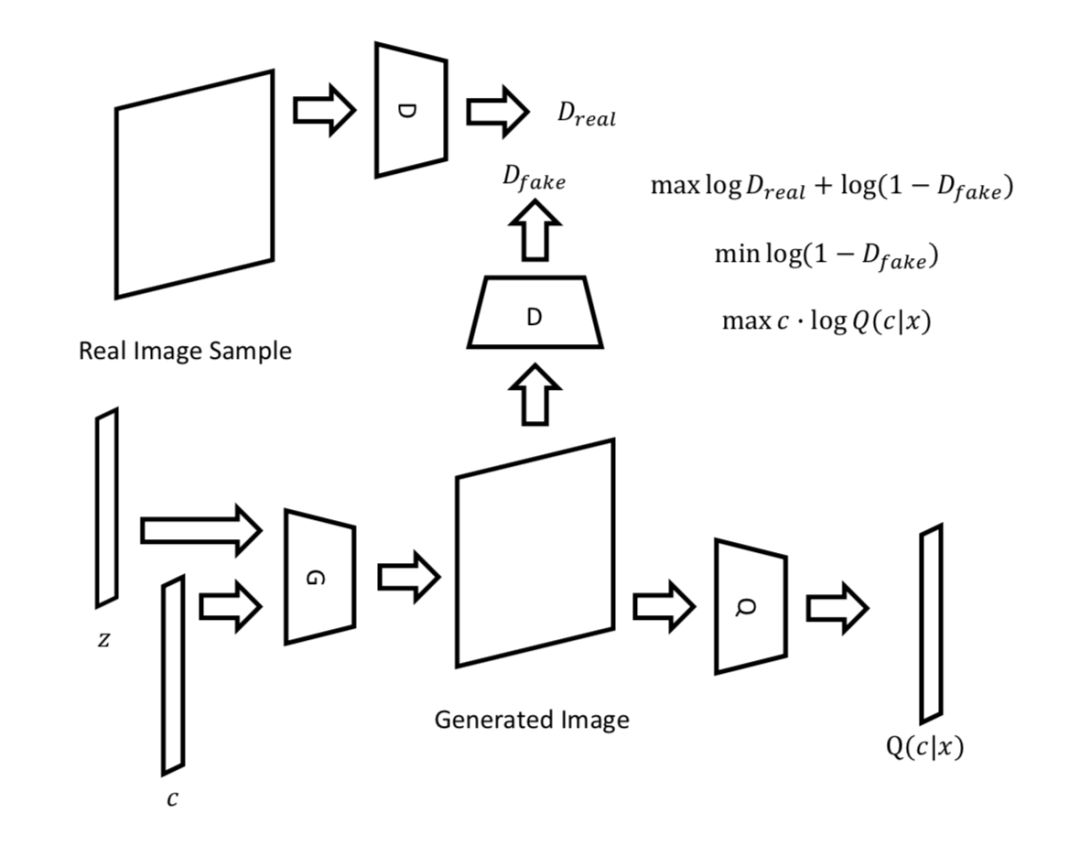
▲ 图1. InfoGAN的整体结构图
由上面的,对于一个极大化互信息的问题转化为一个极大化互信息下界的问题,我们接下来就可以定义:
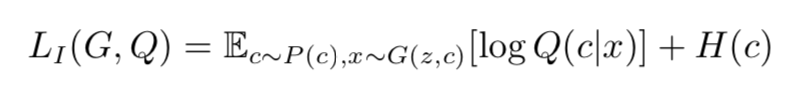
在论文的附录中,作者证明了:
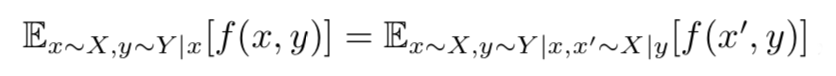
于是:
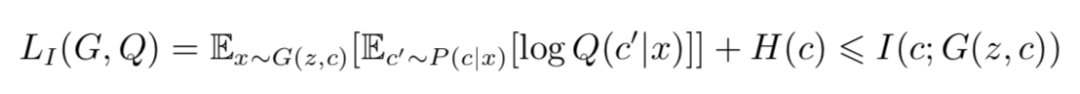
故 LI (G, Q) 是互信息的一个下界。作者指出,用蒙特卡罗模拟(Monte Carlo simulation)去逼近 LI (G, Q) 是较为方便的,这样我们的优化问题就可以表示为:
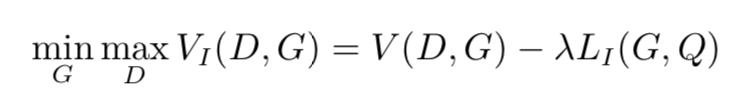
实现
在实现中,D(x)、G(z, c) 和 Q(x) 分别用一个 CNN (Convolutional Neural Networks)、CNN、DCNN (DeConv Neural Networks) 来实现。同时,潜码 c 也包含两部分:一部分是类别,服从 Cat(K = N,p = 1/N),其中 N 为类别数量;另一部分是连续的与生成数据有关的参数,服从 Unif(−1,1) 的分布。
在此应指出,Q(c|x) 可以表示为一个神经网络 Q(x) 的输出。对于输入随机变量 z 和类别潜码 c,实际的 LI(G, Q) 可以表示为:
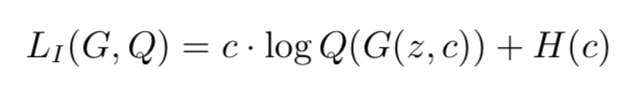
其中 · 表示内积(inner product),c 是一个选择计算哪个 log 的参数,例如 ci = 1 而 cj = 0(∀j = 1,2,···,i − 1,i + 1,···,n),那么 z 这时候计算出的 LI(G,Q) 就等于 log(Q(z,c)i)。这里我们可以消去 H(c),因为 c 的分布是固定的,即优化目标与 H(c) 无关:
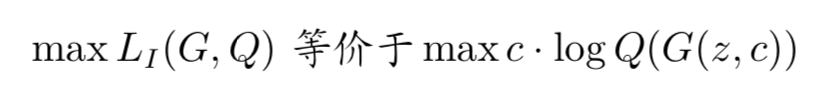
而对于参数潜码,我们假设它符合正态分布,神经网络 Q(x) 则输出其预测出的该潜码的均值和标准差, 我们知道,对于均值 μ,标准差 σ 的随机变量,其概率密度函数为:
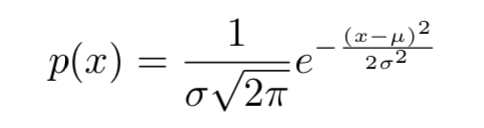
要计算参数潜码 c 的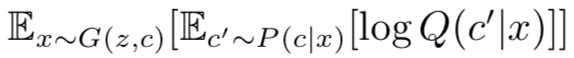 ,就是要计算 log p(c),即:
,就是要计算 log p(c),即:

设 Q(x) 输出的参数潜码 c 的均值 μ,标准差 σ 分别为 Q(x)μ 和 Q(x)σ,那么对于参数潜码 c:
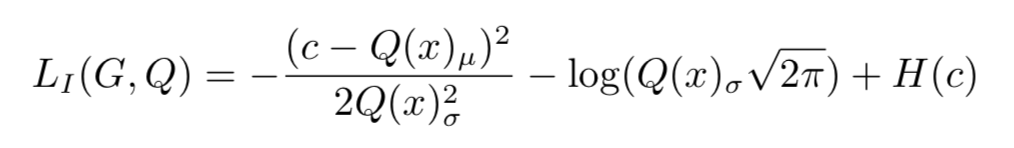
同样的,我们可以消去 H(c),因为 c 的分布是固定的,那么:
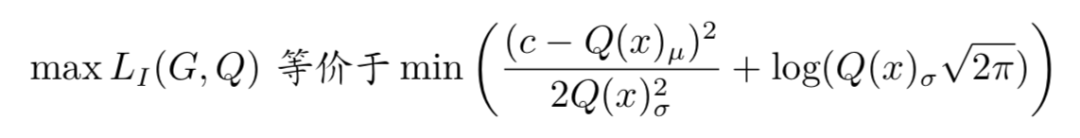
实验
首先,通过和普通的 GAN 比较 LI ,作者证明了 InfoGAN 确实能够优化这一互信息的下界 2。
作者在 MNIST 手写数字数据集(3)、3D 面部数据集(4)、3D 椅子数据集(5)、SVHN 街景房号数据集(6)以及 CelebA 人脸数据集(7)上进行了模型的相关测试。

▲ 图2. MNIST手写字符数据集上的结果
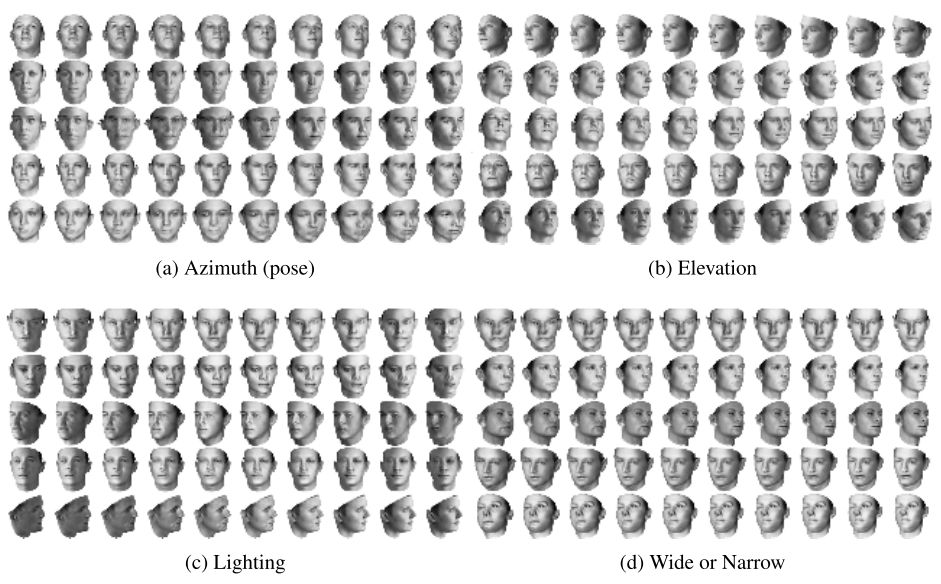
▲ 图3. 3D面部数据集上的结果

▲ 图4. 3D椅子数据集上的结果

▲ 图5. SVHN街景房号数据集上的结果

▲ 图6. CelebA人脸数据集上的结果
作者展示了这些数据集上学习到的类别潜码(从上至下变化)和参数潜码(从左至右变化,由 -2 到 2),我们可以看出,InfoGAN 不仅能够很好地学习数据之间的类型差别,也能够很好地学习到数据本身的一些易于区分的特点,而且生成模型对这些特点的泛化能力还是很好的。
再论InfoGAN的LI
读完论文,我们发现,对于类别潜码,这个 LI 本质上是 x 与 G(z, c) 之间的 KL 散度:
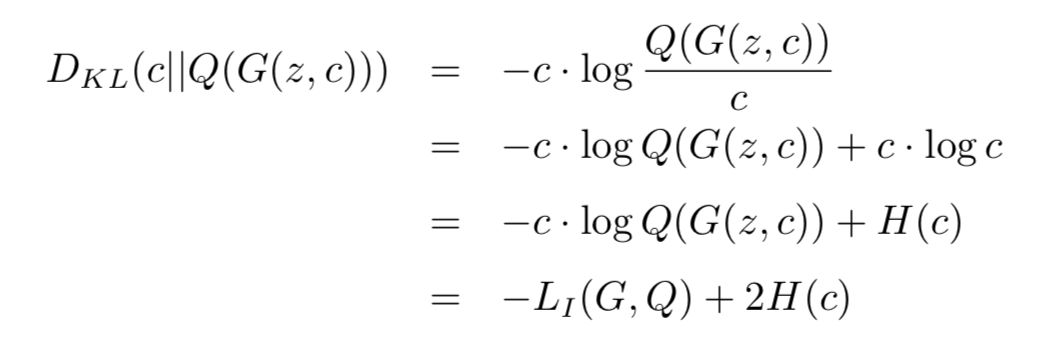
也就是说:
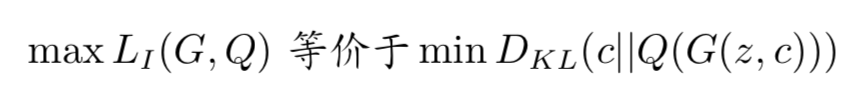
而 min DKL(c||Q(G(z, c))) 意味着减小 c 与 Q(G(z, c)) 的差别。
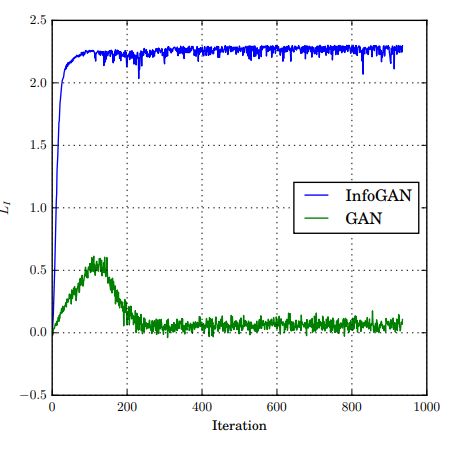
▲ 图7. 普通GAN和InfoGAN的LI在训练过程中的比较
如果我们不考虑 Q(x)σ 的影响,LI 的优化过程:

而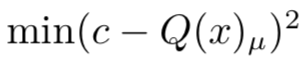 也意味着减小 c 与 Q(G(z, c))μ 的差。
也意味着减小 c 与 Q(G(z, c))μ 的差。
再纵观整个模型,我们会发现这一对 LI 优化的过程,实质上是以 G 为编码器(Encoder), Q 为解码器(Decoder),生成的图像作为我们要编码的码(code),训练一个自编码器(Autoencoder),也就是说,作者口中的信息论优化问题,本质上是无监督训练问题。
关于PaddlePaddle
在 PaddlePaddle 中,一个极为重要的概念即是 fluid.Program(),在官方文档里常见的 exe.run(program= fluid.default_startup_program())的 fluid.default_startup_program() 就是其中一个例子。
在这一使用中可以了解到,我们要用 exe.run() 中的 program 参数运行指定的 fluid.Program(),而官方文档指出,当该参数未指定时,会运行 fluid.default_main_program(),而 fluid.default_main_program() 代表的是未指定 fluid.Program() 的所有操作。
注意,这里说的是“所有”,由于 PaddlePaddle 没有计算依赖检测机制,即使在计算 fetch_list 中的值的时候不会用到操作也会被计算,这一点与 TensorFlow 极其不同,作者本人在使用过程中踩了很大的坑,还望各位注意。在执行多种任务的时候不要一股脑全部写在 fluid.default_main_program() 之中, 这样极其浪费资源,也容易造成一些问题。
一个新的 fluid.Program() 被创建之后,可以在 fluid.program_guard() 中指定该 fluid.Program() 中的操作与变量:
PaddlePaddle 中还需要注意的一点是,fluid.Variable 的命名空间是全局的,也就是说在同一或者不同 fluid. Program() 间,同名(fluid.Variable 的 name 属性相同)的 fluid.Variable 所指向的变量是相同的,所以同一名称在同一或者不同 fluid.Program () 中可以被使用多次,而不用担心 TensorFlow 中会出现的 reuse 问题。
要对一个操作的中的权值的名称进行定义(权值命名为 W1,偏置命名为 b1):
要在之后使用这些 fluid.Variable,例如在 Optimizer 中使用:
在构建完基本的运算操作后,便可以开始初始化操作了:
初始化完成后,可以开始训练啦:
GAN实现
生成对抗网络(Generative Adversarial Nets)是一类新兴的生成模型,由两部分组成:一部分是判别模型(discriminator)D(·),用来判别输入数据是真实数据还是生成出来的数据;另一部分是是生成模型(generator)G(·),由输入的噪声生成目标数据。GAN 的优化问题可以表示为:
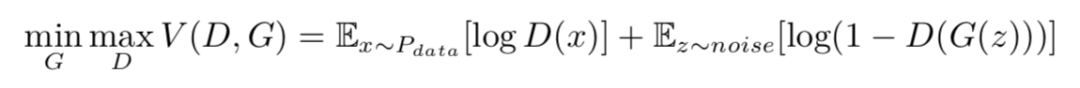
其中 Pdata 是生成样本,noise 是随机噪声。我们用一个双层的 MLP 来演示:
通常,一个 GAN 的训练由两部分组成,第一部分是对 D(·) 进行训练,极大化目标函数:
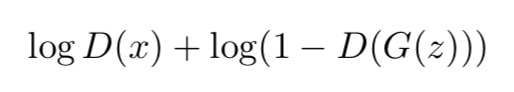
第二部分是对 G(·) 进行训练,极小化目标函数:
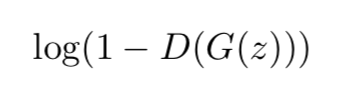
以下是两部分优化的定义:
在定义好这些之后,是时候开训练了:
若欲测试模型效果,可再定义一个 Inference:
然后再这样获取 samples:
后记
本文先前于今年 8 月完成,共享于 PaddlePaddle 论文复现群内,在 10 月 LSGAN 的复现公开之 后,参考该复现更改了模型参数命名和参数列表的实现方法,在此感谢 Todd 同学的复现对本文的帮助。
转载来源:PaperWeekly

本文分享 CSDN - 飞桨PaddlePaddle。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。

