前言
数据结构,一门数据处理的艺术,精巧的结构在一个又一个算法下发挥着他们无与伦比的高效和精密之美,在为信息技术打下坚实地基的同时,也令无数开发者和探索者为之着迷。
也因如此,它作为博主大二上学期最重要的必修课出现了。由于大家对于上学期C++系列博文的支持,我打算将这门课的笔记也写作系列博文,既用于整理、消化,也用于同各位交流、展示数据结构的美。
此系列文章,将会分成两条主线,一条“数据结构基础”,一条“数据结构拓展”。“数据结构基础”主要以记录课上内容为主,“拓展”则是以课上内容为基础的更加高深的数据结构或相关应用知识。
欢迎关注博主,一起交流、学习、进步,往期的文章将会放在文末。
简述
图论,毋庸置疑是数据结构知识体系中的一颗璀璨的明星,是几种逻辑结构中复杂性最高,最变化莫测的结构。因此在初学时众多角度不同的问题总是会成为各式各样的绊脚石。拓扑序列、最短路径、最小生成树…等等等等
而学习计算机科学专业画风的图论与数学专业画风的图论有着大相径庭的方向。很显然,计算机学家更注重图论算法的表示和实现而数学家更倾向于研究图论高级的性质。
在众多计算机领域需要讨论的图论内容中。图的存储结构及其遍历方法无疑是一切算法实现的起点。
俗话说:基础不牢,地动山摇。在所有基础图论算法学习过程中遇到的阻碍,都能在其中或多或少地窥到对存储和遍历内容掌握不牢的身影。

所以,下面就让我们来夯实基础,梳理一下几种存储结构之下的两种遍历方案吧~
下文的内容会与图的存储结构紧密相关,对于常用图的存储掌握不熟悉的同学们可以先观看上一篇文章:图的存储结构
深度优先遍历
深度优先遍历,英文全称叫做" d e e p f i r s t s e a r c h deep first search deep first search",简称" D F S DFS DFS"。
所谓深度优先,就是每次向着更深层次的结点走,走到尽头再进行回溯的遍历方案。
这种遍历方案具有递归调用自身的显著特征,所以在实现时,也常常是使用递归结构。
单单堆砌概念很难精准把握其意思,我们还是抓紧上代码开始实战吧,哦吼。
在开始遍历之前,还是要有一些前置约定:
- 遍历过的点打上标记不用再遍历,可以使用如下的一个数组来完成这个任务
bool vis[N];
//vis[k] = true 表示结点k被遍历过
//vis[k] = false 表示结点k未被遍历过
- 该图为有向无权图
邻接矩阵
使用邻接矩阵存储的图,在寻找可遍历的子节点时特点就是需要枚举所有结点查看是否存在边。
我们约定邻接矩阵定义如下:
bool am[N][N];
//am[x][y] = true 表示x到y之间存在边
那么遍历图的递归程序的基本结构实现如下:
void dfs(int k){//当前结点
vis[k] = true;//该点被遍历过,打上标记
for(int i = 1;i <= n;i++){
if(!am[k][i]){//如果k与i之间没有边相连,则跳过
continue;
}
if(vis[i]){//如果该节点已经被遍历过,则跳过
continue;
}
dfs(i);//遍历更深层次的结点,完成该节点遍历后再进行其他后继节点遍历
}
}
邻接表
使用邻接表存储图的一大特点就是将每个结点可到达的结点信息分开存储在各自的链表中,而非像邻接矩阵一样存储在同一个二维矩阵中。
每个链表的链首被统一记录在一个头结点数组中,我们给定邻接表定义如下:
struct Edge{//边链表结点
int vertex;//边终点
//如果有权值可以继续添加字段
Edge * next;//链表后继指针
};
Edge * head[N];//链首数组,存储所有链表头结点
那么遍历过程如下:
void dfs(int k){
vis[k] = true;//标记遍历过
for(Edge * edge = head[k];edge != NULL;edge = edge->next){
if(vis[edge->vertex]){//如果终点已经被遍历过则跳过
continue;
}
dfs(edge->vertex);
}
}
数组邻接表
数组模拟的邻接表的特点就是放弃了动态内存的管理,而使用已经声明好的数组静态内存来管理边结点的加入。他仍然是链表结构,但不再使用指针获取后继元素位置,取而代之的是使用在数组中的下标来表示。
数组的邻接表定义如下:
struct Edge{
int vertex;//终点
int next;//后继边结点在数组中的下标,0为空
};
Edge nxt[M];//存放边结点的数组
int head[N];//存放各节点边链表头结点的数组
int tot;//边结点计数
那么dfs的实现如下:
void dfs(int k){
vis[k] = true;//节点被遍历过,打上标记
for(int i = head[k];i != 0;i++){
if(vis[nxt[i].vertex]){
continue;
}
dfs(nxt[i].vertex);
}
}
经典应用:有向图判定环
有向图找环其实是个老生常谈的问题,他非常的常见,也有很多的变体,包括寻找最大环,负环等等。
使用深度优先遍历的一大特点就是每次只能遍历一条线路上的结点,路线上结点的先后次序呈现栈的结构。
根据这一特点,如果某个结点的后继在当前栈中则可以说明遍历过程中寻找到了一个环。
所以只需要将上文的遍历方案稍加改造,加入一个全局的判定数组用以标记结点是否在栈中,当遍历到结点时将其入栈,遍历结束后将其出栈。
这里还需要注意区分栈的标记数组和是否遍历的标记数组,他们的功能并不相同。
同时需要函数增加一个返回值,表示有没有寻找到环
存储结构采用邻接表:
bool stack[N];//标记结点是否位于栈中
bool dfs(int k){
vis[k] = true;//标记该节点遍历过
stack[k] = true;//结点入栈
for(Node * node = head[k];node != NULL;node = node->next){
if(stack[node->vertex]){//判断后继节点是否在栈中,如果在,则找到一个环
return true;
}
if(vis[node->vertex]){//如果该节点已经被遍历,则跳过
continue;
}
if(dfs(node->vertex)){//遍历后继节点,如果后继节点找到环,则直接放回true
return true;
}
}
stack[k] = false;//结点出栈
return false;//没有找到环
}
广度优先遍历
广度优先遍历,英文全称为" b r e a d t h f i r s t s e a r c h breadth first search breadth first search",简称 B F S BFS BFS
宽度优先的意思是优先遍历同一层次的结点,当一个层次的结点遍历完了,再遍历下一层次的结点。这与深度优先遍历的方案恰好相对。
有意思的是,不仅是逻辑结构上相对,在结点次序对应的数据结构上,他们也分别对应两个特殊的线性结构——栈和队列。
在上文中我们说深度优先遍历对应的结点次序结构是一种栈,现在的广度优先遍历结点次序对应的就是队列了。准确说,这个队列是预遍历序列,他们只是按照顺序等待被遍历。
如下图:

之所以说这个结构是一个队列,一个重要的原因是这些结点不是预先放置在线性表中的,而是在遍历过程中添加进去的。当遍历第k层结点时,将其子节点加入队尾,当遍历完整个第k层时,后方的所有结点就都是k+1层的结点了。
邻接矩阵
我们说,实现广度优先遍历的关键是实现队列,那么为了方便演示。队列就是用数组和两个动态下标表示:
int queue[N];//队列数组
int l = 1;//队首
int r = 0;//队尾
k = queue[l++];//获取出队元素
queue[++r] = k;//入队元素
同时为了防止结点被多次加入队列而多次被遍历,我们还要加入一个数组,用以标记结点已经进入队列。
bool inQueue[N];//标记结点是否已经入队
那么,使用邻接矩阵存储的图,使用广度优先遍历的方式如下:
int k;
while(l <= r){//队列不为空条件
k = queue[l++];
for(int i = 1;i <= n;i++){
if(!dis[k][i]){//如果没有边,跳过
continue;
}
if(inQueue[i]){//如果该节点已经加入队列,跳过
continue;
}
//结点i入栈
inQueue[i] = true;
queue[++r] = i;
}
}
邻接表
我们应该清楚,在目前的遍历规则下,结点队列和图的存储结构是两个不同的维度,相互之间的影响非常有限。因此改变的图的存储结构,从邻接矩阵改变为邻接表对于遍历实现的影响也非常小,只需要改变访问子节点的方式即可:
int k;
while(l <= r){
k = queue[l++];
for(Edge * edge = head[k];edge != NULL;edge = edge->next){
if(inQueue[edge->vertex]){
continue;
}
inQueue[i] = true;
queue[++r] = edge->vertex;
}
}
数组邻接表
int k;
while(l <= r){
k = queue[l++];
for(int i = head[k];i != 0;i = nxt[i].next){
if(inQueue[nxt[i].vertex){
continue;
}
inQueue[i] = true;
queue[++r] = nxt[i].vertex;
}
}
经典应用:最短合法路径
宽度优先遍历的特点就是其按照层次进行遍历。在寻求最短路径的问题上也有着自己独特的优势。尤其是我们现在要讨论的问题:无权图的最短合法路径
这类问题非常的常见,一个经典的例子是迷宫游戏

但是这里不说这个模型,迷宫的规则总是复杂的,有权的迷宫也不在少数,所以不妨来讨论一个更简单且异曲同工的模型:

在上图中,从点1出发,到达终点点7,最短的一条路需要走多少步。
在这个问题中,到达终点的路径可能有很多,肉眼看去,答案显而易见为 1 − > 6 − > 7 1->6->7 1−>6−>7,需要两步。
如果使用深度优先遍历的话,即使找到了一条通往终点的路径,但是在没有穷尽所有可能的前提下,无法确定其最短方案是否就是当前的一种。所以深度优先遍历只能一点点的记录答案最小值,不断地迭代更新。
但使用宽度优先遍历的方案,问题就变得不一样了,因为无论怎么遍历,第一次出现的终点结点的层数一定是最小的,其方案也一定是最短的,这样就可以将解决方案优化。
对于上图来说,这意味着如果我们将1定义为第0层的话,那么7最早在第二层出现。
下面就让我们使用代码来实现它吧:
输入格式:
第一行为四个整数n,m,s,t,表示点数和边数以及起点和终点,保证终点能够到达
接下来m行,每行两个整数x,y,表示结点x和y之间存在一条边
输出格式:
一个整数表示起点到终点的最短距离
#include<iostream>
using namespace std;
const int N = 2000;
struct Edge{
int vertex;//终点
Edge * next;
Edge(int vertex,Edge * next){//构造函数
this->vertex = vertex;
this->next = next;
}
};
Edge * head[N];//链表头结点数组
int deep[N];//结点深度
bool inQueue[N];//是否进入过队列
int queue[N];//队列
void link(int x,int y){//建立双向边
Edge * edge;
edge = new Edge(y,head[x]);
head[x] = edge;
edge = new Edge(x,head[y]);
head[y] = edge;
}
int main(){
int n,m,s,t;
cin >> n >> m >> s >> t;
for(int i = 0,x,y;i < m;i++){//建边
cin >> x >> y;
link(x,y);
}
int l = 1,r = 0;
int k;
queue[++r] = s;
inQueue[s] = true;
while(l <= r){//遍历队列
k = queue[l++];
if(k == t){//如果出队元素为终点,则找到答案
break;
}
for(Edge * edge = head[k];edge != NULL;edge = edge->next){//遍历下一层结点
if(inQueue[edge->vertex]){//如果该节点已经进入过队列,跳过
continue;
}
queue[++r] = edge->vertex;//结点入队
inQueue[edge->vertex] = true;
deep[edge->vertex] = deep[k] + 1;//计算该节点深度
}
}
cout << deep[t];
}
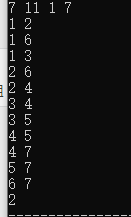
运行,结果如下:
往期博客
- 【数据结构基础】数据结构基础概念
- 【数据结构基础】线性数据结构——线性表概念 及 数组的封装
- 【数据结构基础】线性数据结构——三种链表的总结及封装
- 【数据结构基础】线性数据结构——栈和队列的总结及封装(C和java)
- 【算法与数据结构基础】模式匹配问题与KMP算法
- 【数据结构与算法基础】二叉树与其遍历序列的互化 附代码实现(C和java)
- 【数据结构与算法拓展】 单调队列原理及代码实现
- 【数据结构基础】图的存储结构
- 【数据结构与算法基础】并查集原理、封装实现及例题解析(C和java)
- 【数据结构与算法拓展】二叉堆原理、实现与例题(C和java)
- 【数据结构与算法基础】哈夫曼树与哈夫曼编码(C++)
- 【数据结构与算法基础】最短路径问题
- 【数据结构与算法基础】堆排序原理及实现
- 【数据结构与算法基础】最小生成树算法原理及实现
