什么是并行计算?
并行计算(Parallel Computing)是指同时使用多种计算资源解决计算问题的过程,是 提高计算机系统计算速度和处理能力的一种有效手段。它的基本思想是用多个处理器来 协同求解同一问题,即将被求解的问题分解成若干个部分,各部分均由一个独立的处理 机来并行计算。并行计算系统既可以是专门设计的、含有多个处理器的超级计算机,也 可以是以某种方式互连的若干台的独立计算机构成的集群。通过并行计算集群完成数据 的处理,再将处理的结果返回给用户。
并行计算可分为时间上的并行和空间上的并行。
时间上的并行:是指流水线技术,比如说工厂生产食品的时候步骤分为:
1. 清洗:将食品冲洗干净。
2. 消毒:将食品进行消毒处理。
3. 切割:将食品切成小块。
4. 包装:将食品装入包装袋。
如果不采用流水线,一个食品完成上述四个步骤后,下一个食品才进行处理,耗时且影 响效率。但是采用流水线技术,就可以同时处理四个食品。这就是并行算法中的时间并 行,在同一时间启动两个或两个以上的操作,大大提高计算性能。
空间上的并行:是指多个处理机并发的执行计算,即通过网络将两个以上的处理机连接起来,达到同时计算同一个任务的不同部分,或者单个处理机无法解决的大型问题。
与10.110.12.29mask 255.255.255.224属于同一网段的主机IP地址有哪些?
根据你提供的ip地址和掩码计算出来的ip地址段为10.110.12.0/27.
也就是从10.110.12.0到10.110.12.31.
讲一讲Makefile的内容.
target - 目标文件, 可以是 Object File, 也可以是可执行文件
prerequisites - 生成 target 所需要的文件或者目标
command - make需要执行的命令 (任意的shell命令), Makefile中的命令必须 以 [tab] 开头
显示规则 :: 说明如何生成一个或多个目标文件(包括 生成的文件, 文件的依赖文件, 生成的命令)
隐晦规则 :: make的自动推导功能所执行的规则
变量定义 :: Makefile中定义的变量
文件指示 :: Makefile中引用其他Makefile; 指定Makefile中有效部分; 定义一个多行命令
注释 :: Makefile只有行注释 “#”, 如果要使用或者输出"#"字符, 需要进行转义, “#”
最后,还值得一提的是,在Makefile中的命令,必须要以[Tab]键开始。
讲一讲C++的内联函数
内联函数inline:引入内联函数的目的是为了解决程序中函数调用的效率问题,这么说吧,程序在编译器编译的时候,编译器将程序中出现的内联函数的调用表达式用内联函数的函数体进行替换,而对于其他的函数,都是在运行时候才被替代。这其实就是个空间代价换时间的i节省。所以内联函数一般都是1-5行的小函数。在使用内联函数时要留神:
1.在内联函数内不允许使用循环语句和开关语句;
2.内联函数的定义必须出现在内联函数第一次调用之前;
3.类结构中所在的类说明内部定义的函数是内联函数。
vector, deque, list, set, map底层数据结构 vector(向量)——STL中标准而安全的数组。只能在vector 的“前面”增加数据。
deque(双端队列double-ended queue)——在功能上和vector相似,但是可以在前后 两端向其中添加数据。
list(列表)——游标一次只可以移动一步。如果你对链表已经很熟悉,那么STL中的list 则是一个双向链表(每个节点有指向前驱和指向后继的两个指针)。
set(集合)——包含了经过排序了的数据,这些数据的值(value)必须是唯一的。
map (映射)——经过排序了的二元组的集合,map中的每个元素都是由两个值组成, 其中的key(键值,一个map中的键值必须是唯一的)是在排序或搜索时使用,它 的值可以在容器中重新获取;而另一个值是该元素关联的数值。比如,除了可以 ar[43] = "overripe"这样找到一个数据,map还可以通过ar[“banana”] = "overripe"这 样的方法找到一个数据。如果你想获得其中的元素信息,通过输入元素的全名就可 以轻松实现。
宏定义的优缺点
优点:
-
提高了程序的可读性,同时也方便进行修改;
-
提高程序的运行效率:使用带参的宏定义既可完成函数调用的功能,又能避免函数的出栈与入栈操作,减少系统开销,提高运行效率;
3.宏是由预处理器处理的,通过字符串操作可以完成很多编译器无法实现的功能。比如##连接符。
缺点:
-
由于是直接嵌入的,所以代码可能相对多一点;
-
嵌套定义过多可能会影响程序的可读性,而且很容易出错;
-
对带参的宏而言,由于是直接替换,并不会检查参数是否合法,存在安全隐患。

bfs和dfs如何遍历
1.深度优先搜索(DFS)
原文里的深度优先搜索代码是有问题的,那是中序遍历的推广,而深度优先搜索是先序遍历的推广,我这里把两种代码都给出来,深度优先搜索的非递归实现使用了一个栈。
深度优先遍历图的方法是,从图中某顶点v出发:
a.访问顶点v;
b.依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
c.若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
用一副图来表达这个流程如下:
1).从v = 顶点1开始出发,先访问顶点1
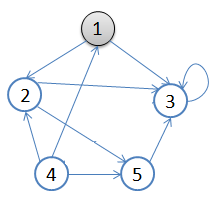
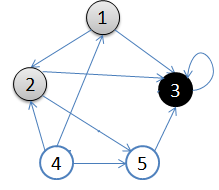
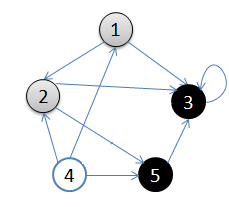
2).按深度优先搜索递归访问v的某个未被访问的邻接点2,顶点2结束后,应该访问3或5中的某一个,这里为顶点3,此时顶点3不再有出度,因此回溯到顶点2,再访问顶点2的另一个邻接点5,由于顶点5的唯一一条边的弧头为3,已经访问了,所以此时继续回溯到顶点1,找顶点1的其他邻接点。
上图可以用邻接矩阵来表示为:
int maze[][] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};
具体的代码如下:
import java.util.LinkedList;
import classEnhance.EnhanceModual;
public class DepthFirst extends EnhanceModual {
@Override
public void internalEntrance() {
// TODO Auto-generated method stub
int maze[][] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 0, 1 },
{ 0, 0, 1, 0, 0 },
{ 1, 1, 0, 0, 1 },
{ 0, 0, 1, 0, 0 }
};
dfs(maze, 1);
}
public void dfs(int[][] adjacentArr, int start) {
int nodeNum = adjacentArr.length;
if (start <= 0 || start > nodeNum || (nodeNum == 1 && start != 1)) {
System.out.println("Wrong input !");
return;
} else if (nodeNum == 1 && start == 1) {
System.out.println(adjacentArr[0][0]);
return;
}
int[] visited = new int[nodeNum + 1];//0表示结点尚未入栈,也未访问
LinkedList<Integer> stack = new LinkedList<Integer>();
stack.push(start);
visited[start] = 1;//1表示入栈
while (!stack.isEmpty()) {
int nodeIndex = stack.peek();
boolean flag = false;
if(visited[nodeIndex] != 2){
System.out.println(nodeIndex);
visited[nodeIndex] = 2;//2表示结点被访问
}
//沿某一条路径走到无邻接点的顶点
for (int i = 0; i < nodeNum; i++) {
if (adjacentArr[nodeIndex - 1][i] == 1 &&
visited[i + 1] == 0) {
flag = true;
stack.push(i + 1);
visited[i + 1] = 1;
break;//这里的break不能掉!!!!
}
}
//回溯
if(!flag){
int visitedNodeIndex = stack.pop();
}
}
}
}
广度优先搜索(BFS)
广度优先搜索是按层来处理顶点,距离开始点最近的那些顶点首先被访问,而最远的那些顶点则最后被访问,这个和树的层序变量很像,BFS的代码使用了一个队列。搜索步骤:
a .首先选择一个顶点作为起始顶点,并将其染成灰色,其余顶点为白色。
b. 将起始顶点放入队列中。
c. 从队列首部选出一个顶点,并找出所有与之邻接的顶点,将找到的邻接顶点放入队列尾部,将已访问过顶点涂成黑色,没访问过的顶点是白色。如果顶点的颜色是灰色,表示已经发现并且放入了队列,如果顶点的颜色是白色,表示还没有发现
d. 按照同样的方法处理队列中的下一个顶点。
基本就是出队的顶点变成黑色,在队列里的是灰色,还没入队的是白色。
用一副图来表达这个流程如下:
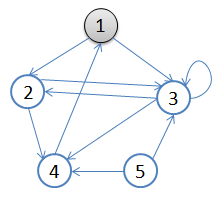
1.初始状态,从顶点1开始,队列={1}
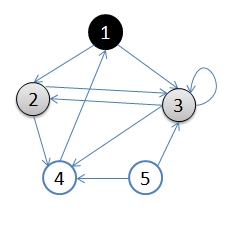
2.访问1的邻接顶点,1出队变黑,2,3入队,队列={2,3,}
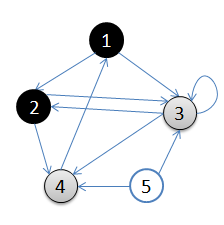
3.访问2的邻接顶点,2出队,4入队,队列={3,4}
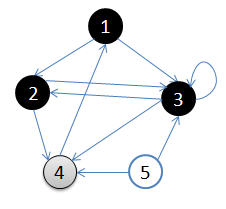
4.访问3的邻接顶点,3出队,队列={4}
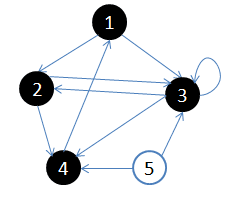
5.访问4的邻接顶点,4出队,队列={ 空}
分析:
从顶点1开始进行广度优先搜索:
初始状态,从顶点1开始,队列={1}
访问1的邻接顶点,1出队变黑,2,3入队,队列={2,3,}
访问2的邻接顶点,2出队,4入队,队列={3,4}
访问3的邻接顶点,3出队,队列={4}
访问4的邻接顶点,4出队,队列={ 空}
顶点5对于1来说不可达。
上面图可以用如下邻接矩阵来表示:
int maze[][] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 1, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0 }
};
具体的代码如下,这段代码有两个功能,bfs()函数求出从某顶点出发的搜索结果,minPath()函数求从某一顶点出发到另一顶点的最短距离:
import java.util.LinkedList;
import classEnhance.EnhanceModual;
public class BreadthFirst extends EnhanceModual {
@Override
public void internalEntrance() {
// TODO Auto-generated method stub
int maze[][] = {
{ 0, 1, 1, 0, 0 },
{ 0, 0, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 1, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0 }
};
bfs(maze, 5);//从顶点5开始搜索图
int start = 5;
int[] result = minPath(maze, start);
for(int i = 1; i < result.length; i++){
if(result[i] !=5 ){
System.out.println("从顶点" + start +"到顶点" +
i + "的最短距离为:" + result[i]);
}else{
System.out.println("从顶点" + start +"到顶点" +
i + "不可达");
}
}
}
public void bfs(int[][] adjacentArr, int start) {
int nodeNum = adjacentArr.length;
if (start <= 0 || start > nodeNum || (nodeNum == 1 && start != 1)) {
System.out.println("Wrong input !");
return;
} else if (nodeNum == 1 && start == 1) {
System.out.println(adjacentArr[0][0]);
return;
}
//0表示顶点尚未入队,也未访问,注意这里位置0空出来了
int[] visited = new int[nodeNum + 1];
LinkedList<Integer> queue = new LinkedList<Integer>();
queue.offer(start);
visited[start] = 1;//1表示入队
while (!queue.isEmpty()) {
int nodeIndex = queue.poll();
System.out.println(nodeIndex);
visited[nodeIndex] = 2;//2表示顶点被访问
for (int i = 0; i < nodeNum; i++) {
if (adjacentArr[nodeIndex - 1][i] == 1 &&
visited[i + 1] == 0) {
queue.offer(i + 1);
visited[i + 1] = 1;
}
}
}
}
/*
* 从start顶点出发,到图里各个顶点的最短路径
*/
public int[] minPath(int[][] adjacentArr, int start) {
int nodeNum = adjacentArr.length;
LinkedList<Integer> queue = new LinkedList<Integer>();
queue.offer(start);
int path = 0;
int[] nodePath = new int[nodeNum + 1];
for (int i = 0; i < nodePath.length; i++) {
nodePath[i] = nodeNum;
}
nodePath[start] = 0;
int incount = 1;
int outcount = 0;
int tempcount = 0;
while (path < nodeNum) {
path++;
while (incount > outcount) {
int nodeIndex = queue.poll();
outcount++;
for (int i = 0; i < nodeNum; i++) {
if (adjacentArr[nodeIndex - 1][i] == 1 &&
nodePath[i + 1] == nodeNum) {
queue.offer(i + 1);
tempcount++;
nodePath[i + 1] = path;
}
}
}
incount = tempcount;
tempcount = 0;
outcount = 0;
}
return nodePath;
}
}
CPU如果访问内存?
通过内存管理单元(MMU)
先看一张简单的CPU访问内存的流程图:
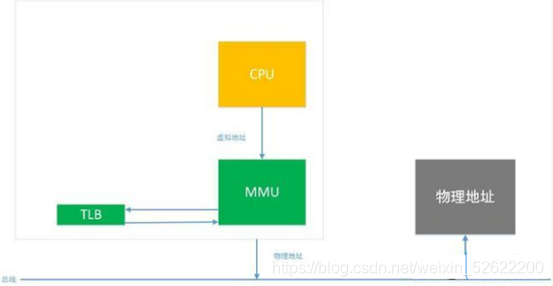
TLB:转换lookaside 缓存,有了它可以让虚拟地址到物理地址转换速度大增。
从上图中可以清楚的知道了,CPU,DDR,MMU它们三者之间的关系。CPU在MMU开启的情况下,访问的都是虚拟地址。
首先通过MMU将虚拟地址转换为物理地址,
然后再通过总线上去访问内存(我们都知道内存是挂在总线上的)。
那MMU是怎么将虚拟地址转换为物理地址呢?当然是通过页表的方式。MMU从页表中查出虚拟地址对应的物理地址是什么,然后就去访问物理内存了。
找出在A数组中,B数组中没有的数字,在B数组中,A数组中没有的数字
```cpp
public static void find(int arr[],int[]b){
HashMap<Integer,Integer> map = new HashMap<Integer, Integer>();
for (int i = 0; i < arr.length; i++) {
map.put(arr[i],0);
}
for (int i=0;i<b.length;i++) {
if(map.containsKey(b[i])){
map.put(b[i],1);
}else{
System.out.println("在B数组中A不存在的数字");
System.out.println(b[i]);
}
}
for (int i = 0; i <arr.length ; i++) {
if(map.get(arr[i])==0){
System.out.println("在A数组中存在的,在B数组不存在的数字");
System.out.println(arr[i]);
}
}
}
