闻理似悟,遇境则迷!!!
栈与队列来说也算是一种特殊的线性表,栈的特点是后进先出,队列的特点是先进先出。
栈
栈的特点是后进先出,栈的操作只有出栈和入栈(也叫压栈),除此之外,还包含栈顶与栈底的指向以及栈的长度。
因此栈的定义如下
public class ZStack {
/**
* 栈顶指向
*/
private int top = 0;
/**
* 栈底指向
*/
private int bottom = 0;
/**
* 栈长度
*/
public int length = 0;
/**
* 栈内数据
*/
private Object[] datas;
/**
* 栈内最大空间
*/
public int MAX_SIZE = 100;
/**
* 出栈
*
* @return
*/
public Object pop() {
// 栈顶与栈底指向同一个位置
if (top == 0) {
return null;
} else {
// 栈顶下移
top--;
// 取出栈顶数据
Object data = datas[top];
// 栈顶置为空
datas[top] = null;
length--;
return data;
}
}
/**
* 入栈
*
* @param o
*/
public void push(Object o) {
if (top < MAX_SIZE){
datas[top] = o;
top++;
length++;
}else {
throw new OutOfMemoryError("栈已满,不能再加了");
}
}
// 初始化栈
public ZStack() {
// 默认栈长度为100
datas = new Object[MAX_SIZE];
}
}
进制转换(十进制转二进制)
将十进制转为二进制
第一步,将该数除以二,取余,将余数入栈
第二步,重复第一步,直到最后除数为0或者1
第三步,依次出栈,最后的顺序就是二进制数
例如 11转为二进制
11 %2 = 5.,…1
5 % 2 = 2…1
2 % 2 =1…0
入栈顺序 1 1 0 1,最后输出 1 0 1 1,验证一下,1 + 2 +0 +8 = 11
核心代码如下
// 初始化栈
ZStack zStack = new ZStack();
while (num > 0) {
// 余数入栈
zStack.push(num % 2);
num = num / 2;
if (num == 1) {
zStack.push(num);
num = 0;
}
}
// 出栈,打印出二进制内容
StringBuffer sb =new StringBuffer();
while (zStack.length > 0) {
sb.append(zStack.pop());
}
中缀表达式转后缀表达式
逆波兰表达式就是后缀表达式,举个例子吧,我们要计算1+(2-3)*4,转为后缀表达式就是 1 2 3 - 4 * +,怎么来的呢
计算规则如下:
第一步,如果是数字,直接输出
第二步,如果是表达式符号,入栈,入栈需要对符号优先级进行判断,如果当前运算符优先级小于栈顶元素,需要先出栈顶元素,然后再入栈
第三步,如果是(,直接入栈,
第四步,如果是),依次出栈,直到遇到(或者栈为空
第五步,将栈内剩余符号出栈
例子,
1>>> 栈 [],输出(1)
+>>>栈[+],输出(1)
(>>>栈[+ ,( ],输出(1)
2>>>栈[+ ,( ],输出(1 2)
->>>栈[+ ,( ,- ],输出(1 2)
3>>>栈[+ ,(, - ],输出(1 2 3)
)>>> 栈[+],输出(1 2 3 -)
× >>> 栈[+,×],输出(1 2 3 -)
4 >>> 栈[+,×],输出(1 2 3 - 4)
最后输出(1 2 3 - 4 + ×)
1+(2*3 - 4)/ 1
1>>> 栈 [],输出(1)
+>>>栈[+],输出(1)
(>>>栈[+ ,( ],输出(1)
2>>>栈[+ ,( ],输出(1 2)
× >>>栈[+ ,(,× ],输出(1 2)
3 >>>栈[+ ,(,× ],输出(1 2 3)
_ >>>栈[+ ,(,- ],输出(1 2 3 ×)注意,×出栈了
4 >>>栈[+ ,(,- ],输出(1 2 3 × 4)
) >>>栈[+ ],输出(1 2 3 × 4 -)
/ >>>栈[+ ,/ ],输出(1 2 3 × 4 -)
1>>>栈[+ ,/ ],输出(1 2 3 × 4 -1)
最后输出1 2 3 × 4 -1/+
验证
核心代码
private static String parseSuffixExpression(String next) {
StringBuffer suffixSb = new StringBuffer();
char[] chars = next.toCharArray();
ZStack zStack = new ZStack();
for (int i = 0; i < chars.length; i++) {
char thisChar = chars[i];
// 判断字符是否是数字,如果是数字,直接输出
if (Character.isDigit(thisChar)) {
suffixSb.append(thisChar);
} else if (thisChar == ')') {
/**
* 当入栈时是)时,栈为空时依次出栈,栈不为空依次出栈,直到遇到(停止
*/
// 栈为空
if (zStack.length == 0) {
zStack.push(thisChar);
} else {
Object pop = zStack.pop();
while (pop != null && !String.valueOf(pop).equals("(")) {
suffixSb.append(pop);
pop = zStack.pop();
}
}
} else if (thisChar == '+' || thisChar == '-') {
/**
* 当为+,或者-入栈时,需要与栈顶元素的优先级比较,优先级高的需要先出栈,直到遇到(或者栈为空
*/
// 栈为空,直接push
if (zStack.length == 0) {
zStack.push(thisChar);
} else {
Object pop = zStack.pop();
while (pop!=null && !String.valueOf(pop).equals("(")){
suffixSb.append(pop);
pop = zStack.pop();
}
/**
* (出栈了,需要重新入栈,重点
*/
if (String.valueOf(pop).equals("(")){
zStack.push("(");
}
zStack.push(thisChar);
}
} else if (thisChar == '*' || thisChar == '/' || thisChar == '(') {
/**
* 为* ,/,( 直接入栈
*/
zStack.push(thisChar);
} else {
System.err.println("输入错误");
}
}
/**
* 输出栈内其它元素
*/
while (zStack.length!=0) {
suffixSb.append(zStack.pop());
}
return suffixSb.toString();
}
RPN(逆波兰表达式)
上面介绍了中缀表达式转后缀表达式(波兰表达式),这里主要是讲波兰表达式如何计算为我们想要的值,以上面例子讲解计算规则
一句来说就是,数字入栈,遇到运算符将栈顶两个元素出栈,运算后再入栈。
例 1 2 3 × 4 -1/+
前3为数字 栈 1 2 3
× >>> 栈1 6
4 >>>> 栈 1 6 4
->>> 1 2
1>>> 1 2 1
/ >>>1 2
+ 1+2 = 3(结果)
与上图结果吻合
核心代码
/**
* 逆波兰表达式计算器,输入的是一个波兰表达式
* @param next
*/
private static void rpn(String next) {
if (!next.isEmpty()) {
ZStack zStack = new ZStack();
char[] chars = next.toCharArray();
for (int i = 0; i < chars.length; i++) {
char thisChar = chars[i];
// 判断字符是否是数字,如果是数字,就入栈
if (Character.isDigit(thisChar)) {
zStack.push(thisChar);
} else {
// 先出的是后面的操作数
Double behind = Double.parseDouble(String.valueOf(zStack.pop()));
Double front = Double.parseDouble(String.valueOf(zStack.pop()));
switch (thisChar) {
case '+':
zStack.push(front + behind);
break;
case '-':
zStack.push(front - behind);
break;
case '*':
zStack.push(front * behind);
break;
case '/':
if (behind == 0) {
throw new NumberFormatException("被除数不能为0");
}
zStack.push(front / behind);
break;
default:
break;
}
}
}
System.out.println(next + "计算结果为:" + zStack.pop());
}
}
这里还有很多bug,例如,只支持10以内的计算(一个字符),还有一些特殊输入没有判断,反正我是比较满意的,哈哈。
队列
队列是一种先进先出的数据结构。就像我们在食堂打饭排队一样,每次入队列都在队尾操作,每次出队列就在队头操作。使用java代码实现如下,队列使用链式存储结构实现比较好,我这里采用的是顺序存储结构,通过队头队尾形成一个环状队列。
/**
* 队列类实现(顺序存储实现)
*/
public class ZQueue {
// 当前队列长度
private int length = 0;
// 队列最大长度
private int MAX_SIZE = 5;
// 队列数据
private Object[] datas;
/**
* 队头索引
*/
private int head = 0;
/**
* 队尾索引
*/
private int tail = 0;
/**
* 出队列操作
*
* @return
*/
public Object delete() {
Object returnObj = new Object();
if (head == tail) {
if (datas[head] == null) {
System.err.println("队列已空,不能出队列");
;
} else {
returnObj = datas[head];
datas[head] = null;
}
} else {
/**
* 队列头置为空,将头往后移
*/
returnObj = datas[head];
datas[head] = null;
head = (head + 1) % MAX_SIZE;
}
length--;
return returnObj;
}
/**
* 入队列操作
*/
public void add(Object obj) {
if (length == MAX_SIZE) {
System.err.println("队列已满,不能入队");
} else {
// 队尾累加,如果到顶了,头尾相接,再从头开始,形成一个循环队列
datas[tail++ % MAX_SIZE] = obj;
length++;
}
}
public ZQueue() {
this.datas = new Object[MAX_SIZE];
}
}
主类
ZQueue zQueue = new ZQueue();
zQueue.add("1");
zQueue.add("2");
zQueue.delete();
zQueue.add("3");
zQueue.add("4");
zQueue.add("5");
zQueue.add("6");
Object delete = zQueue.delete();
zQueue.add("7");
运行结果
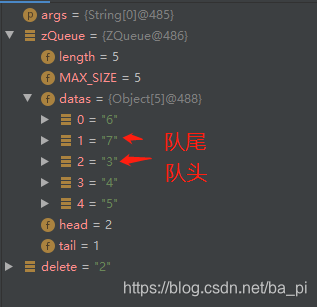
以上就是栈与队列相关的操作,最后附上git地址: https://gitee.com/zhoujie1/data-structure-and-algorithm.git
顺便提一个有趣的事情,昨天一前端同事问道将一堆数组平均分成3份的问题,当时我脑海里闪过通过通过快慢指针的方式,定义3个指针,一个指针每次+1,一个指针每次+2,一个指针每次+3,当走得最快的指针到达数组结尾,剩余两个指针的位置就将整个数据分成了3份,从而达到了目的。此时我也深深的感受到了算法的魅力,也坚定了我往下走的决心。
