广度优先搜索

图算法——广度优先搜索（breadth-first search，BFS）。
 广度优先搜索指出是否有从A到B的路径。

 如果有，广度优先搜索将找出最短路径。

你需要在你们的朋友中，找到一位芒果销售商。检查名单中的每个人时，你都将其朋友加入名单。

这样一来，你不仅在朋友中查找，还在朋友的朋友中查找。别忘了，你的目标是在你的人际

关系网中找到一位芒果销售商。因此，如果Alice不是芒果销售商，就将其朋友也加入到名单中。
这意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网，直
到找到芒果销售商。这就是广度优先搜索算法。

一度关系胜过二度关系，二度关系胜过三度关系，以此类推。因此，你应先在一度关系中搜索，

确定其中没有芒果销售商后，才在二度关系中搜索。广度优先搜索就是这样做的！

在广度优先搜索的执行过程中，搜索范围从起点开始逐渐向外延伸，即先检查一度关系，再检查二度关系。

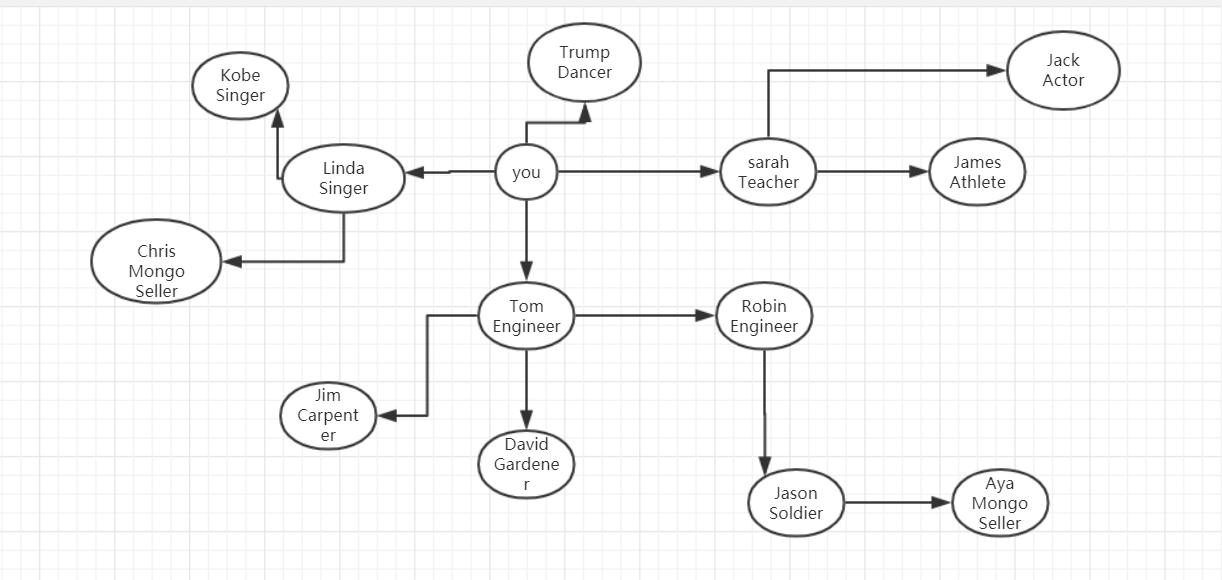
 在you 的人际关系中找到最近的Mongo Seller

使用队列的数据结构，广度优先搜索，python 代码如下：

#!/usr/bin/env python
# -*- coding: utf-8 -*-

' breadth first search '
__author__ = 'chris'

from collections import deque
graph = {}
graph['you'] = [{'name':'Tom','profession':'Engineer'},{'name':'Sarah','profession':'Teacher'},
                {'name':'Linda','profession':'Singer'},{'name':'Trump','profession':'Dancer'},]
graph['Sarah'] = [{'name':'Jack','profession':'Actor'},{'name':'James','profession':'Athlete'},]
graph['Linda'] = [{'name':'Kobe','profession':'Singer'},{'name':'Chris','profession':'Mongo Seller'},]
graph['Tom'] = [{'name':'Jim','profession':'Carpenter'},{'name':'David','profession':'Gardener'},
                {'name': 'Robin', 'profession': 'Engineer'},]
graph['Robin'] = [{'name':'Jason','profession':'Solider'}]
graph['Jason'] = [{'name':'Aya','profession':'Mongo Seller'}]

search_deque = deque()# 声明一个队列
search_deque.extend(graph['you']) # 将你自己朋友加入到队列中

while search_deque:
    person = search_deque.popleft()
    if person['profession'] == 'Mongo Seller':
        print('关系最近的Mongo Seller是'+ person['name'])
        break
    else:
         if person['name'] in graph.keys():
             search_deque.extend(graph[person['name']])

如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是
从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。
你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，
即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为
O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点（vertice）数，E为边数