1,归并排序是建立在归并操作上的一种有效的排序算法。该算法也是采用分治法(Divide and Conquer)的一个非常典型的应用。
难点在于分治,分治是将原有数列分成一个个小的的有序数列,然后再合并。
2,例如集合{7,6,5,4,3,2,1},分治归并的逻辑如下:
groupsize = 1:
建立一个临时数组,将{7,6}进行排序
{6,7}
↓
写入到原有数列
{6,7,5,4,3,2,1}
新建一个临时数组,将{5,4}进行排序
{4,5}
↓
写入到原有数列
{6,7,4,5,3,2,1}
新建一个临时数组,将{3,2}进行排序
{2,3}
↓
写入到原有数列
{6,7,4,5,2,3,1}
新建一个临时数组,将{1}进行排序
{1}
↓
写入到原有数列
{6,7,4,5,2,3,1}
groupsize = 2:
新建一个临时数组,将{6,7,4,5}进行排序
{4,5,6,7}
↓
写入到原有数列
{4,5,6,7,2,3,1}
新建一个临时数组,将{2,3,1}进行排序
{1,2,3}
↓
写入到原有数列
{4,5,6,7,1,2,3}
groupsize = 4:
新建一个临时数组,将{4,5,6,7,1,2,3}进行排序
{1,2,3,4,5,6,7}
↓
写入到原有数列
{1,2,3,4,5,6,7}
3,详见代码并解析
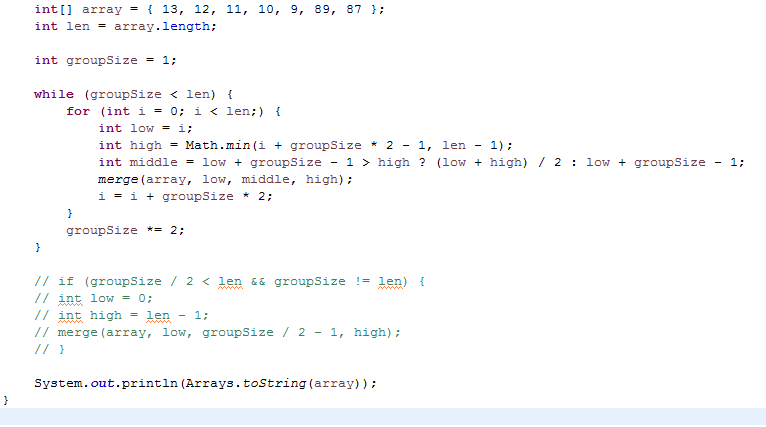

第一轮:groupSize = 1,autoArray.length = 2;(临时的集合用来放置将要排序的分治的数列)
{13,12,11,10,9,8,7,6,5,4,3,2,1}
↓
{12,13,11,10,9,8,7,6,5,4,3,2,1}
↓
{12,13,10,11,9,8,7,6,5,4,3,2,1}
↓
{12,13,10,11,8,9,7,6,5,4,3,2,1}
↓
{12,13,10,11,8,9,6,7,5,4,3,2,1}
↓
{12,13,10,11,8,9,6,7,4,5,3,2,1}
↓
{12,13,10,11,8,9,6,7,4,5,2,3,1}
↓
{12,13,10,11,8,9,6,7,4,5,2,3,1} autoArray.length = 1; 只剩下最后一个数了
第二轮: groupSize = 2,autoArray.length = 4
↓
{10,11,12,13,8,9,6,7,4,5,2,3,1}
↓
{10,11,12,13,6,7,8,9,4,5,2,3,1}
↓
{10,11,12,13,6,7,8,9,2,3,4,5,1}
↓
{10,11,12,13,6,7,8,9,2,3,4,5,1} autoArray.length = 1; 只剩下最后一个数了
第三轮:groupSize = 4,autoArray.length = 8
↓
{6,7,8,9,10,11,12,13,2,3,4,5,1}
↓
{6,7,8,9,10,11,12,13,1,2,3,4,5} autoArray.length = 5; 只剩下最后五个数了
第四轮:groupSize = 8,autoArray.length = 13
{1,2,3,4,5,6,7,8,9,10,11,12,13,}
上部分代码是视为分治,下部分视为归并。
归并是建立在分治的基础上,归并的前提是两个要归并的数列都是两个按要求排序的有序数列。
因此刚开始的归并是从两个长度各自为1 开始的。
private static void merge(int[] array, int low, int middle, int high) {
}
array:源数列
low:源数列中即将排序的两个有序数列中最小的下标
middle:前一个有序数列中最后一位数的下标
high:源数列中即将排序的两个有序数列中最大的下标
例如:
2,6 4,554
low:0
middle:1
high:3
再如:
2,4,5,8 3,7
low:0
middle:3
high:5
所以在第一轮merge的时候,是以两个长度分别为1的有序数列开始的
13,12
merge的时候,会建一个数组,大小为两个数列长度之和,所以本次数组长度为2,
比较两个数列首部的下标index1 index2
源数列 【】 【】
index1/low /middle index2/high
临时数组 【】 【】
归并方法: 比较index1 和 index2 两个数列中最小的值,因为两个数列的长度可能不一样,所以需要限定条件,
index1<=middle 同时 index2 <= high 的情况
刚开始一定是满足这个条件的,找出最小的之后,放入到临时数组中,同时下标加1,下次就不会再比较,可能一个数列全部都比较小,然后就全部放入到临时数组中了,
那另一个数列也要将剩下的放进去,所以需要有两个判断条件
当:index1<= middle,将左边的剩余数全部写入
当:index2 <= high,将右边的剩余数全部写入
分治中:middle:前一个有序数列中最后一位数的下标,所以一般是low + groupSize - 1
但是当low + groupSize - 1 >high 的时候,说明已经超过了源数列的长度,
这时候这部分分治应该是剩余的的最后一段中,且在一个有序的集合中,
{6,7,8,9,10,11,12,13,2,3,4,5,1}
下次排序的时候两个数列分别是2,3,4,5 和1
low应该是8
middle 应该是 11
high应该是12
如果用low+high/2就错了。
但是当
{10,11,12,13,6,7,8,9,2,3,4,5,1}
下次排序的时候两个数列分别是1
low应该是12
middle应该是12
high 是12
如果用low + groupSize - 1就错了
所以需要分类讨论下。