20162308 2017-2018-2 《程序设计与数据结构》第七周学习总结
教材学习内容总结
学习目标
- 理解树抽象数据类型
- 会用树解决问题
- 掌握树的遍历方法
- 掌握二叉树的实现(数组,链表)
- 会用二叉树表示决策树
- 分析Java Collections API中树相关的类
学习内容
树
在前期学习了栈、队列等线性数据结构后,这周我们初步学习和了解了非线性数据结构的知识。
树是由一组结点及一组边构成,结点用来保存元素,边表示结点之间的连接。每个节点都处于树的某一层中。树的根是树的最顶层中唯一的结点。树中只有唯一的根节点。
这里需要区别的是,数据结构中的树和图论中的树,虽然比较类似,但是还是有一些区别。
在图论中,树(英语:Tree)是一種無向圖(undirected graph),其中任意两个顶点间存在唯一一條路径。或者说,只要没有回路的连通图就是树。森林是指互相不交并树的集合。——维基百科
在計算機科學中,樹(英语:tree)是一种抽象数据类型(ADT)或是實作這種抽象数据类型的数据结构,用來模擬具有樹狀結構性質的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。——维基百科
虽然在使用的时候,并不会在意具体的定义,但是我个人认为,在数据结构中所学的树,更侧重于层次上的关系,在图论中,更关注节点之间的连通性。
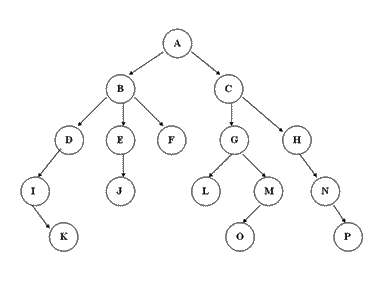
树的分类
- 一般树、二叉树、n叉树
一般来说,子结点的个数没有限制的树称为一般树,每个结点最多有n个结点的树成为n叉树,每个结点最多有两个子结点的树成为二叉树。
-
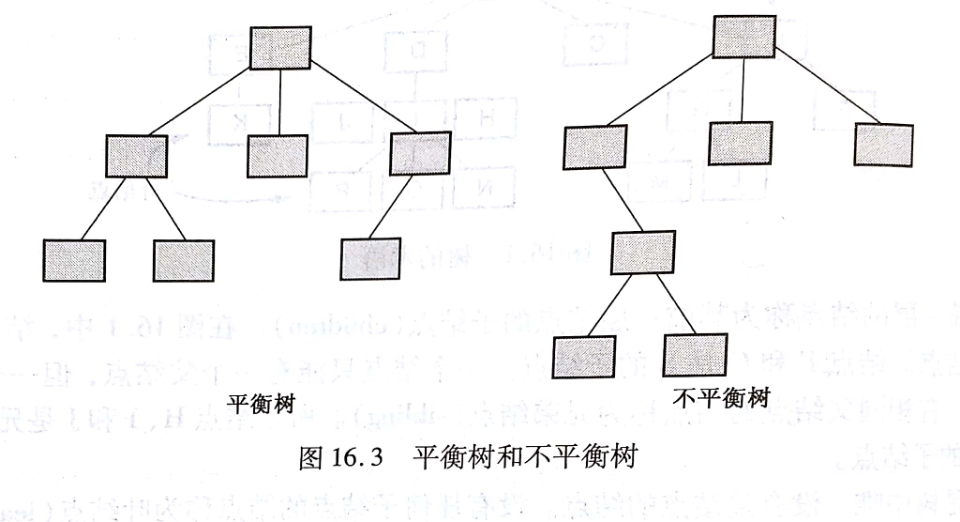
平衡树
如果树的所有子结点都在同一层上,或彼此最多不超过1层,则认为树是平衡的。
-
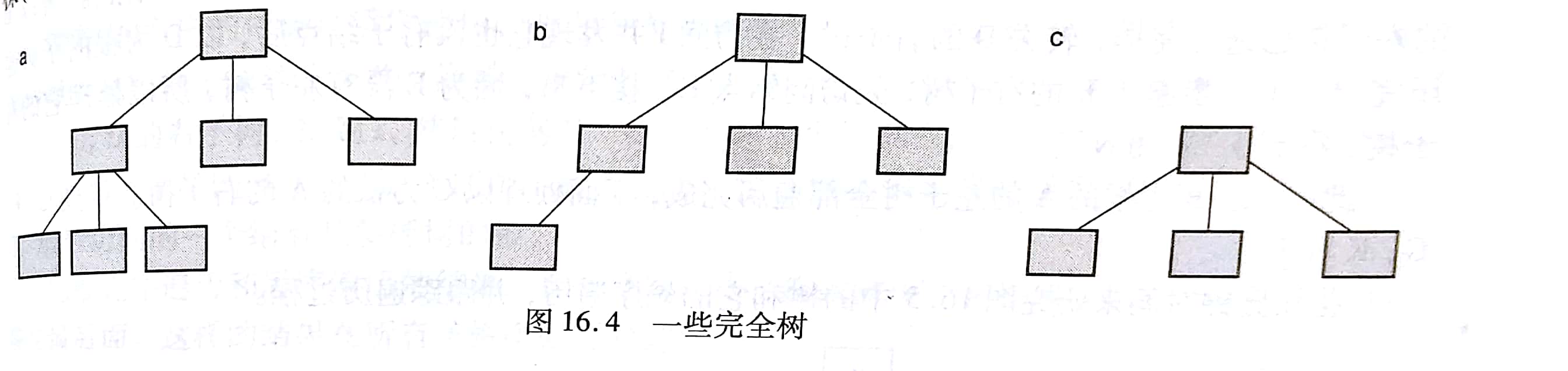
满树、完全树
如果树的所有叶节点都在同一层,并且每个非叶结点都正好有n个子结点,则称n叉树是满树;如果树是满的,或者一直在倒数第二层都是满的且最底层的所有叶结点都位于树的左侧,则称树是完全的。
树的遍历
- 先序、中序及后序
这三个遍历算法的思路基本上是类似的,无非就是添加元素的顺序上存在差异。
public void inorder(ArrayIterator<T> iter){
if(left != null)
left.inorder(iter);
iter.add (element);
if(right != null)
right.inorder(iter);
}
public void preorder(ArrayIterator<T> iter){
iter.add (element);
if(left != null)
left.postorder(iter);
if(right != null)
right.postorder(iter);
}
public void postorder(ArrayIterator<T> iter){
if(left != null)
left.postorder(iter);
if(right != null)
right.postorder(iter);
iter.add (element);
}
- 层序遍历
LinkedQueue<BTNode> queue = new LinkedQueue();
queue.enqueue(tree.getRoot);
while(!queue.isEmpty()){
BTNode temp = queue.dequeue();
queue.enqueue(temp.getLeft());
queue.enqueue(temp.getRight());
}
代码调试中的问题和解决过程
代码托管
- 代码提交过程 & 代码量截图:
结对及互评
点评模板:
- 博客中值得学习的或问题:
其他
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | - | 1 | 10 | |
| 第二周 | - | 2 | 20 | |
| 第三周 | - | 3 | 30 | |
| 第四周 | - | 4 | 40 | |
| 第五周 | - | 5 | 50 |
-
计划学习时间:20小时
-
实际学习时间:10小时
-
改进情况: