7种规格的包装箱要装有两辆铁路平板车上去,包装箱的宽和高相同,但厚度(t,以cm计)和重量( 以kg计)不同,
以kg计)不同,
表A-1给出了每包装箱的厚度、重量和数量,每辆车有10.2m长的地方用来装包装箱(像面包片那样),车的载重为40吨,
对C5、C6、C7、规格的包装箱的总数有一个特殊的限制:这些规格箱子所占的空间(厚度)不能超过302.7cm。
试把包装箱装到两辆平板车上去(图A-6)使得浪费的空间最小。
表A-1 每种包装箱的厚度、重量和数量
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
C7 |
|
|
t(cm) w(kg) n |
48.7 2000 8 |
52.0 3000 7 |
61.3 1000 9 |
72.0 500 6 |
48.7 4000 6 |
52.0 2000 4 |
64.0 1000 8 |

解:
一.设决策变量:
Xij表示第i辆平板车放j类包装箱Xij件
tj为第j个包装箱的厚度(cm)
wj为第j个包装箱的重量(kg)
nj表示第j个包装箱的数量
二.分析约束条件
1. 两辆车上的各种包装箱数量必须小于等于各类包装箱的总数

2.每辆车上的载重必须小于等于400000kg


3.每辆车上包装箱的长度必须小于等于1020cm
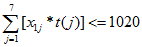

4. C5、C6、C7、规格的包装箱的总厚度不能超过302.7cm

5.包装箱的件数必须是整数
@for(link(i,j) : @gin(x(i,j)));
三.目标函数
[OBJ] min = 2040 - @sum(link(i,j) : x(i,j)*t(j));
四.LinGo代码
model: sets: row/1..2/; col/1..7/ : t, w, n; link(row, col) : x; endsets data: t = 48.7, 52.0, 61.3, 72.0, 48.7, 52.0, 64.0; w = 2000, 3000, 1000, 500, 4000, 2000, 1000; n = 8, 7, 9, 6, 6, 4, 8; enddata @for(col(j) : @sum(row(i) : x(i,j)) <= n(j)); @for(row(i) : @sum(col(j) : x(i,j)*w(j)) <= 400000); @for(row(i) : @sum(col(j) : x(i,j)*t(j)) <= 1020); @sum(row(i) : @sum(col(j) | j#ge#5 : x(i,j) * t(j) )) <= 302.7; @for(link(i,j) : @gin(x(i,j))); [OBJ] min = 2040 - @sum(link(i,j) : x(i,j)*t(j)); end
五.LinGo运算结果
Global optimal solution found.
Objective value: 0.6000000
Objective bound: 0.6000000
Infeasibilities: 0.000000
Extended solver steps: 9342
Total solver iterations: 40250
Variable Value Reduced Cost
T( 1) 48.70000 0.000000
T( 2) 52.00000 0.000000
T( 3) 61.30000 0.000000
T( 4) 72.00000 0.000000
T( 5) 48.70000 0.000000
T( 6) 52.00000 0.000000
T( 7) 64.00000 0.000000
W( 1) 2000.000 0.000000
W( 2) 3000.000 0.000000
W( 3) 1000.000 0.000000
W( 4) 500.0000 0.000000
W( 5) 4000.000 0.000000
W( 6) 2000.000 0.000000
W( 7) 1000.000 0.000000
N( 1) 8.000000 0.000000
N( 2) 7.000000 0.000000
N( 3) 9.000000 0.000000
N( 4) 6.000000 0.000000
N( 5) 6.000000 0.000000
N( 6) 4.000000 0.000000
N( 7) 8.000000 0.000000
X( 1, 1) 8.000000 -48.70000
X( 1, 2) 1.000000 -52.00000
X( 1, 3) 0.000000 -61.30000
X( 1, 4) 6.000000 -72.00000
X( 1, 5) 3.000000 -48.70000
X( 1, 6) 0.000000 -52.00000
X( 1, 7) 0.000000 -64.00000
X( 2, 1) 0.000000 -48.70000
X( 2, 2) 6.000000 -52.00000
X( 2, 3) 9.000000 -61.30000
X( 2, 4) 0.000000 -72.00000
X( 2, 5) 0.000000 -48.70000
X( 2, 6) 3.000000 -52.00000
X( 2, 7) 0.000000 -64.00000
Row Slack or Surplus Dual Price
1 0.000000 0.000000
2 0.000000 0.000000
3 0.000000 0.000000
4 0.000000 0.000000
5 3.000000 0.000000
6 1.000000 0.000000
7 8.000000 0.000000
8 366000.0 0.000000
9 367000.0 0.000000
10 0.3000000 0.000000
11 0.3000000 0.000000
12 0.6000000 0.000000
OBJ 0.6000000 -1.000000
结论:
浪费空间最小为:0.6cm
C1 C2 C3 C4 C5 C6 C7
第一辆 8 1 0 6 3 0 0
第二辆 0 6 9 0 0 3 0