1. simulink仿真设计
震荡信号本质是调制信号,可以表示为:
u(t)=A*(1+m*cos(Ωt+θ))*cos(ωt+φ)=A*cos (ωt+φ)+ A*m*cos(Ωt+θ)*cos(ωt+φ)
使用simulink仿真如下:
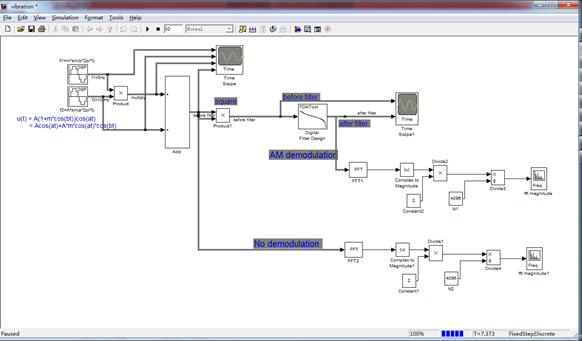
2. 时域信号
时域信号输入设计为信号调制模型。
u(t)=A*(1+m*cos(Ωt+θ))*cos(ωt+φ)=A*cos (ωt+φ)+ A*m*cos(Ωt+θ)*cos(ωt+φ)
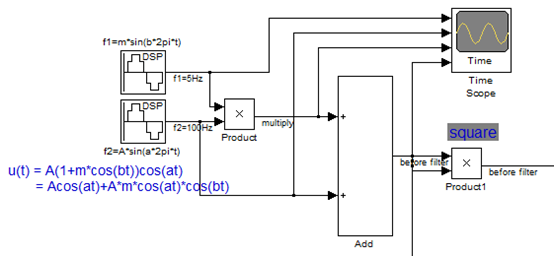
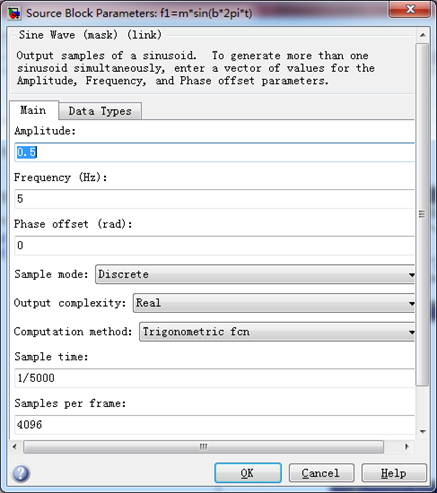
输入信号1: m*cos(Ωt+θ) = 0.5*cos(2*pi*5*t), 调制深度m=0.5, 频率f=5Hz。
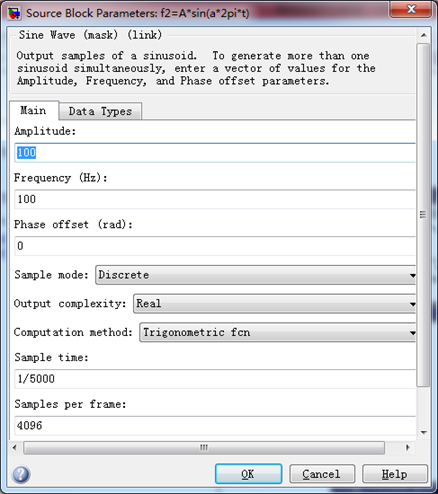
输入信号2: A*cos(Ωt+θ) = 100*cos(2*pi*100*t), 幅值A=100, 频率f=100Hz。
时域信号:
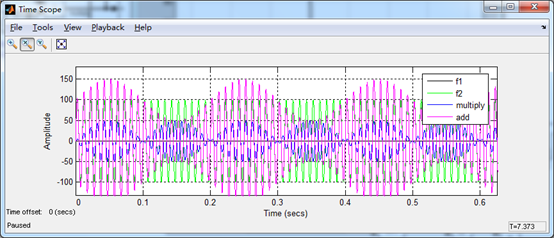
图中,蓝色为相乘后的信号,最大幅度为mA=50, 粉色为叠加后的信号,可见100Hz的信号被5Hz信号调制,信号包络为5Hz。
3. 频域信号
对叠加后的信号进行fft变换。
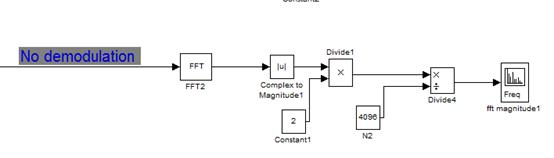
FFT输出为:

中心平率100Hz,幅值100, 左右各有一个侧带波,信号频率为100±5Hz,幅值为25.
为什么会出现这个情况?
u(t)=A*(1+m*cos(Ωt+θ))*cos(ωt+φ)=A*cos (ωt+φ)+ A*m*cos(Ωt+θ)*cos(ωt+φ)
积化和差公式化简后:
u(t)=A*cos(ωt+φ)+0.5*A*m*cos((ω+Ω)t+φ+θ)+0.5*A*m*cos((ω-Ω)t+φ-θ).
如上图,幅值为25的侧带波来源于0.5mA=0.5*0.5*100 = 25,频率是ω+Ω和ω-Ω。
4 . 信号解调
震荡信号会引起测量系统失效,为什么如此呢?
简单的说,信号被调制之后,原基频信号就会以较低频率的震荡信号为包络发生震荡,而测量系统的记录时间长度有限,那么就会造成记录时间段内的波形重建之后,依然不够2倍包络波周期,从时域波形来看,就是测量系统每次计算的数据只是较长包络的一小段。
所以需要对信号进行解调,平方解调是分析震荡信号的有效手段。对叠加后的信号进行低通滤波,排除谐波干扰,然后进行FFT计算。解析过程就是对信号u(t)进行平方,经过简单的积化和差计算,可得平方后调制波Ω出现在2倍频位置,即会出现mA2cos(Ωt+θ)因式。

频域图如下:
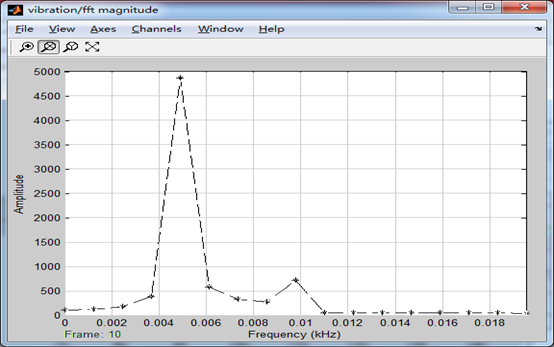
震荡信号在5Hz出,幅度为mA2=0.5*100*100 = 5000。
而200Hz处应该为基波信号,但幅值变得很小是由于中间的滤波器缘故。
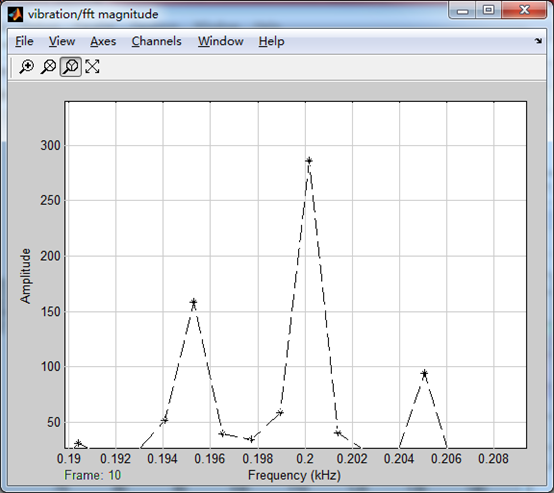
滤波器设计为带通,1Hz-100Hz, 20阶IIR滤波器。
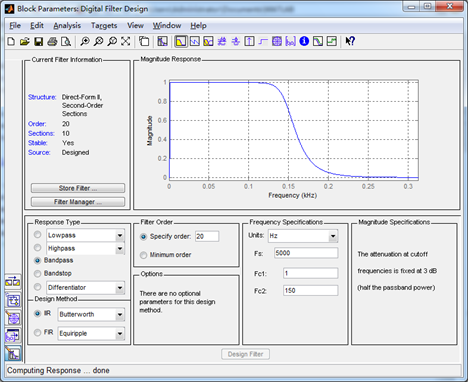
完成仿真后,就可以从FDA Tool生成滤波器系数,然后用C在MCU上实现上述FFT计算和滤波过程,最终解析出震荡信号特征。