Floyd算法
算法解析:因为一张连通图中不是所有点到其他点都是有一条直接路径的,所以我们可以借助别的和终点相连的点到达终点,便是起点-中转....-终点;
以小推大,
小:假设当前只有1可以当中转点,start为起点,end为终点;因此当start点需要借助点1到end点时,便需要进行if(edge[start][end]>edge[start][1]+edge[1][end])的判断,
这个判断的意思就是 :我的起点到终点的路径长度是否比中转方法的长度长,这时我们当然需要优先选择短的路径,并且在edge[start][end]中更新,这样就相当于我们就确定了一条start到end的最佳路径。
大:理解了小例子后,我们就可以去推测图上的其他所有点都可以作为某个start到某个end点的中转点,因此通过不断比较,不断更新edge[start][end],我们最后就可以得到start点到end点的最短距离矩阵。
输入:顶点数,边数;有向图;
输入格式:起点 终点 路径长度; 
样例:4 8
1 2 2
1 3 6
1 4 4
2 3 3
3 1 7
3 4 1
4 1 5
4 3 12
伪代码:

1 Floyd(G){ //伪代码 2 Edge[maxen][maxen];//有向边矩阵 3 int n; //顶点数 4 int m;//边数 5 /*输入图G的顶点、边数、以及各条边的信息*/ 6 for(int k=1;k<=n;k++) 7 for(int i=1;i<=n;i++) 8 for(int j=1;j<=n;j++) 9 if(Edge[i][j]>Edge[i][k]+Edge[k][j]) 10 Edge[i][j]=Edge[i][k]+Edge[k][j]; 11 }
源码

1 #include <stdio.h> 2 #include <iostream> 3 #include <math.h> 4 #include <algorithm> 5 #include <string.h> 6 using namespace std; 7 const int maxen=200; 8 const int Maxx=9999; 9 int edge[maxen][maxen]; 10 void init(int n){ //初始化边矩阵 11 for(int i=1;i<=n;i++){ 12 for(int j=1;j<=n;j++){ 13 if(i!=j) 14 edge[i][j]=Maxx; 15 else 16 edge[i][j]=0; 17 } 18 } 19 } 20 void Floyd(int n){ //弗洛伊德算法 21 for(int k=1;k<=n;k++){ 22 for(int i=1;i<=n;i++){ 23 for(int j=1;j<=n;j++){ 24 if(edge[i][j]>edge[i][k]+edge[k][j]){ 25 edge[i][j]=edge[i][k]+edge[k][j]; 26 } 27 } 28 } 29 } 30 } 31 int main(){ 32 int n,m;//n为起点,m为边数; 33 scanf("%d %d",&n,&m); 34 int s,e,w; 35 init(n); 36 for(int i=1;i<=m;++i){ 37 scanf("%d %d %d",&s,&e,&w); 38 edge[s][e]=w; 39 } 40 Floyd(n); 41 for(int i=1;i<=n;++i){ 42 for(int j=1;j<=n;++j){ 43 printf("s:%d e:%d w:%d ",i,j,edge[i][j]);//输出每条边 44 } 45 printf(" "); 46 } 47 return 0; 48 }
算法时间复杂度:O(n³) 分析:算法需要执行三个嵌套循环,所以需要n³
Dijkstra算法
介绍:用于计算一个节点到其他节点的最短距离的算法。
个人算法分析 1:设两个集合A和B,A中是访问过被收纳入集合的点,B是还未访问过的点;
2:设一个数组visit,这个数组记录每个顶点是否被访问过;
3:先将起点纳入集合A,并且标记访问为true;
4:找出离起点最短距离的边,然后更新图中每个点到起点距离。(就是以找到的这个点为中转点,判断其他点是否能够通过这个点与起点距离拉近)
5:重复步骤4,直至所有点被访问过;
时间复杂度:O(n²)
样例 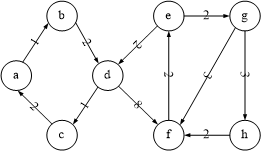
8 11
1 2 1
2 4 2
3 1 2
4 3 1
4 6 8
5 4 2
5 7 2
6 5 2
7 6 3
7 8 3
8 6 2
代码:

1 #include <stdio.h> 2 #include <iostream> 3 #include <math.h> 4 #include <algorithm> 5 #include <string.h> 6 using namespace std; 7 const int maxen=200; 8 const int Maxx=9999; 9 int edge[maxen][maxen];//边矩阵 10 int visit[maxen];//记录被访问过的点 11 int lowcost[maxen];//起到到每条边的最短距离 12 void init(int n){ //初始化 13 for(int i=1;i<=n;++i){ 14 visit[i]=false; 15 lowcost[i]=Maxx; 16 } 17 for(int i=1;i<=n;i++){ 18 for(int j=1;j<=n;j++){ 19 if(i!=j) 20 edge[i][j]=99999; 21 else 22 edge[i][j]=0; 23 } 24 } 25 } 26 void Dijkstra(int start,int n){ 27 for(int i=1;i<=n-1;i++){ //还剩下N-1的点需要去访问 28 int minn=99999; 29 int index=0; 30 for(int j=1;j<=n;j++){ 31 if(minn>lowcost[j]&&visit[j]!=true){ //寻找与起点距离最小且还未访问的点 32 minn=lowcost[j]; 33 index=j; 34 } 35 } 36 visit[index]=true; //标记访问 37 for(int k=1;k<=n;k++){ //更新起点到其他点的距离 38 if(lowcost[k]>lowcost[index]+edge[index][k]){ //这里是lowcost[index]的原因是edge里面的边长不是更新过的边长 39 lowcost[k]=lowcost[index]+edge[index][k]; 40 } 41 } 42 } 43 } 44 int main(void){ 45 int n,m;//顶点数与边数 46 int s,e,w; 47 scanf("%d %d",&n,&m); 48 init(n);//初始化数组 49 for(int i=1;i<=m;i++){ 50 scanf("%d %d %d",&s,&e,&w); 51 edge[s][e]=w; 52 if(s==start) lowcost[e]=w;//记录当前与起点直接相连的点 53 } 54 int start=1;//起点为点1 55 lowcost[start]=0;//起点到本身的距离为0 56 visit[start]=true; //起点标记已访问状态 57 Dijkstra(start,n); 58 printf("%d ",lowcost[8]);//输出点1到点8的距离 59 return 0; 60 }
github:https://github.com/yizhihenpidehou/bananas/tree/master/%E7%AC%AC%E4%BA%8C%E5%91%A8
