POJ3281-Dining(最大流)(拆点)

题意:牧场主为N只牛(1 <= N <= 100)准备了a(1 <= a <= 100)种可以吃的和b(1 <= b <= 100)种可以喝的。每只牛的克隆体都有各自喜欢的食物和饮料，而每种食物或饮料只能分配给一只牛，最多有多少只牛可以同时得到喜欢的食物和饮料？

分析:一只牛只要获得它的喜欢清单中的一种食物和一种饮料就满足了，求最大的牛的数量。我们一种直观的想法是(源---食物---牛---饮料---汇点)，但是这样会有一个如下的问题。
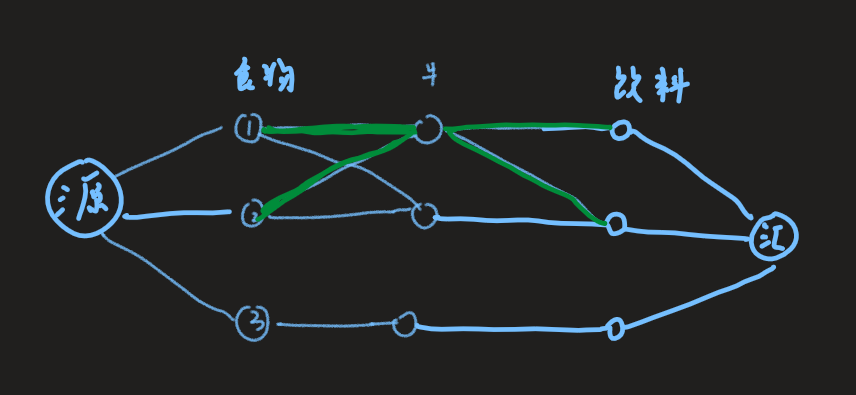就是，从源头提供的食物会经过绿色的边分叉，这样一只牛可以携带多份食物到达终点，我们可以把一只牛拆成两点，在中间加一条(容量为1)的边，这样从左边过来的食物只能有一种。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>

using namespace std;

const int inf = 1 << 29, N = 50005, M = 300005;
int h[N], e[M], ne[M], d[N];
int w[M];

int m, s, t, idx, maxflow;

//n只牛，a种吃的，b种喝的
int n, a, b;

void add(int a, int b, int c)
{
	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
	e[idx] = a, w[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}

//构造分层图
bool bfs()
{
	memset(d, 0, sizeof d);
	queue<int> q;
	q.push(s), d[s] = 1;
	while (q.size())
	{
		int u = q.front();
		q.pop();
		for (int i = h[u]; i != -1; i = ne[i])
		{
			int j = e[i];
			if (w[i] && !d[j])
			{
				q.push(j);
				d[j] = d[u] + 1;
				if (j == t) return true;
			}
		}
	}
	return false;
}

//在分层图上增广
int dinic(int u, int flow)
{
	if (u == t) return flow;
	int rest = flow, k;

	for (int i = h[u]; i != -1 && rest; i = ne[i])
	{
		int j = e[i];
		if (w[i] && d[j] == d[u] + 1)
		{
			k = dinic(j, min(rest, w[i]));
			//增广完毕
			if (!k) d[j] = 0;
			w[i] -= k;
			w[i ^ 1] += k;
			//剩余容量
			rest -= k;
		}
	}
	//返回流过的值
	return flow - rest;
}

int main()
{
	
	scanf("%d%d%d", &n, &a, &b);

	memset(h, -1, sizeof h);
	s = 0, t = a + n + n + b + 1;
	for (int i = 1; i <= n; ++i)
	{
		int f, d;
		scanf("%d%d", &f, &d);
		int u;
		for (int j = 1; j <= f; ++j)
		{
			scanf("%d", &u);
			add(u, a + i, 1);
		}

		for (int j = 1; j <= d; ++j)
		{
			scanf("%d", &u);
			add(a + n + i, a + n + n + u, 1);
		}
		add(a + i, a + n + i, 1);
	}

	for (int i = 1; i <= a; ++i)
	{
		add(0, i, 1);
	}

	for (int i = 1; i <= b; ++i)
	{
		add(a + n + n + i, t, 1);
	}
	
	int flow = 0;
	while (bfs())
	{
		while (flow = dinic(s, inf)) maxflow += flow;
	}

	printf("%d
", maxflow);

	return 0;
}