二叉堆初探

一、二叉堆基础

1. 二叉堆是什么？

二叉堆就是一棵完全二叉树。

什么是完全二叉树？定义d为树的深度，则一棵完全二叉树的前(d-1)层是满的，而第d层的节点从右往左有若干连续缺失。

并且二叉堆有优先级，有的二叉堆每一个父亲都比他的儿子小，称为小根堆；反之称为大根堆。

这样说比较抽象，放一张小根堆的图：

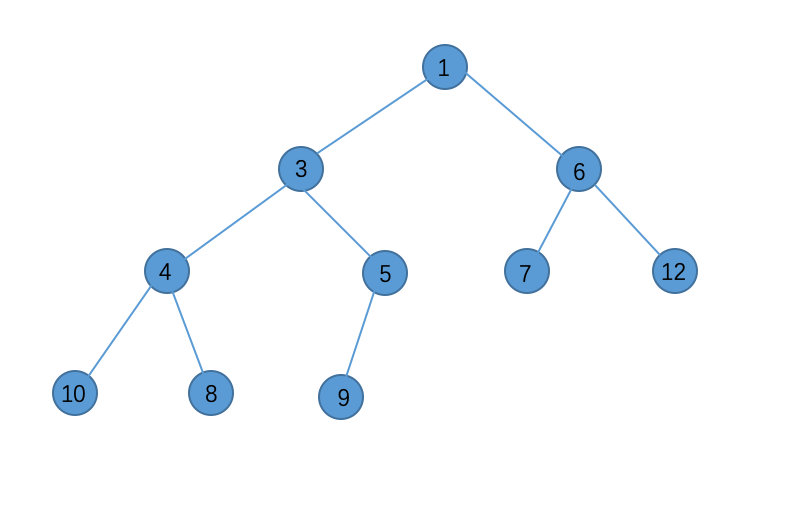
2. 如何存储一个二叉堆？

主要有两种存储方法。

第一种是链表存储，记录左儿子右儿子，父亲与值；

int root=1;//堆顶
int siz;//堆的大小
struct Tree
{
    int ls,rs,fa,val;
}tree[100010];

第二种是用数组存储，开两倍空间，乘2表示左儿子，乘2加1表示右儿子，除以2下取整表示父亲。这种表示方式较为方便。

int siz;//堆的大小
int tree[200020];//tree[1]即为堆顶

之后都用这种写法。堆也默认为小根堆。

3. 二叉堆的操作

注：接下来的实现代码都是实现小根堆的

1. 最基础的操作

就不用说了。时间复杂度\(O(1)\)

inline int top(){return tree[1];}
inline int size(){return siz;}
inline bool empty(){return siz==0;}

2. 堆的插入

在堆底插入，再依次与其父亲作比较，选择是否交换。时间复杂度\(O(\log n)\)

举个例子：向刚刚的小根堆插入数字2。

首先我们在堆底插入2：

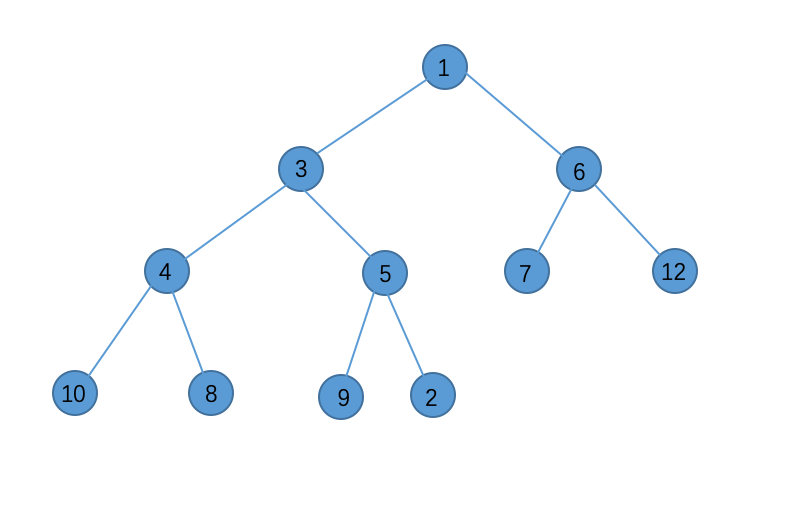
2<5，交换：

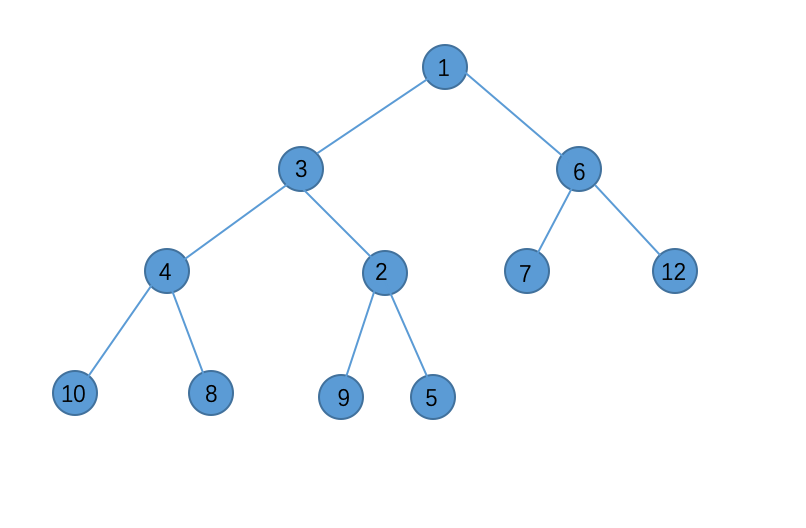
2<3，交换：

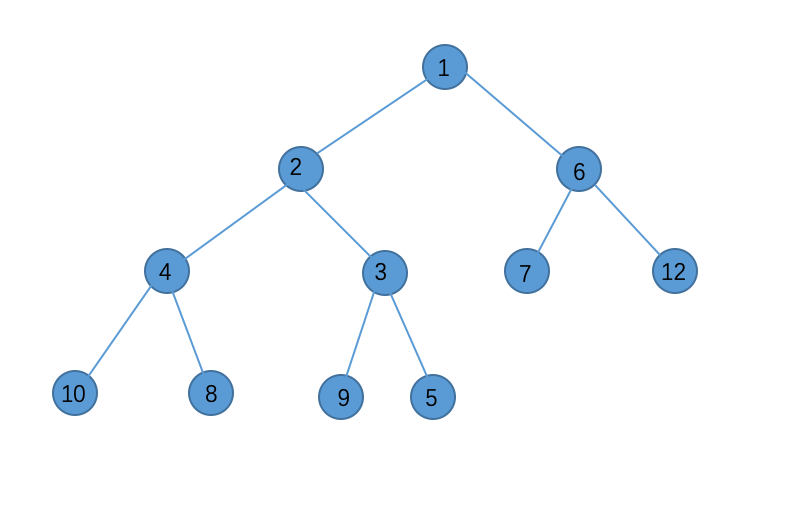
2>1，不能再交换了。

inline void push(int xx)
{
    tree[++siz]=xx;
    int now=siz;
    while(now!=1)
    {
        int nxt=now>>1;
        if(tree[nxt]>tree[now])swap(tree[nxt],tree[now]);
        else break;
        now=nxt;
    }
    return;
}

3. 堆的删除

删除别的元素是没有意义的，故我们只讨论删除堆顶的情况。
先将堆顶堆底交换，删掉堆底，再将堆顶向下判断和哪一个孩子交换。时间复杂度\(O(\log n)\)

还是刚才的例子：我们要删除堆顶1。首先将堆顶堆底交换：

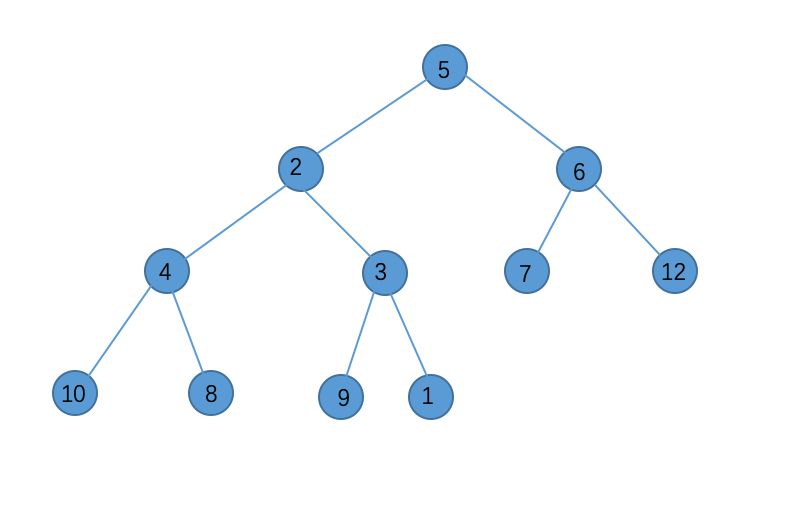
然后把堆底删掉：

接下来我们来进行调整，以保持堆的性质。两个儿子中2更小，故与2交换：

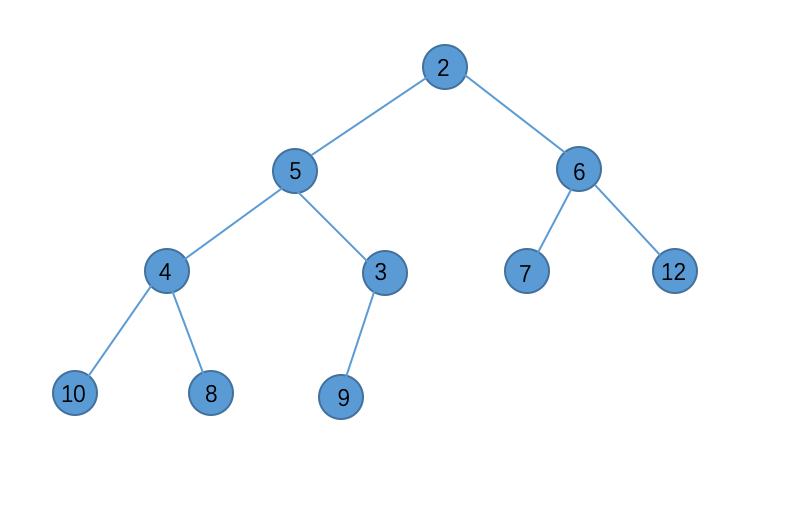
3更小，故与3交换：

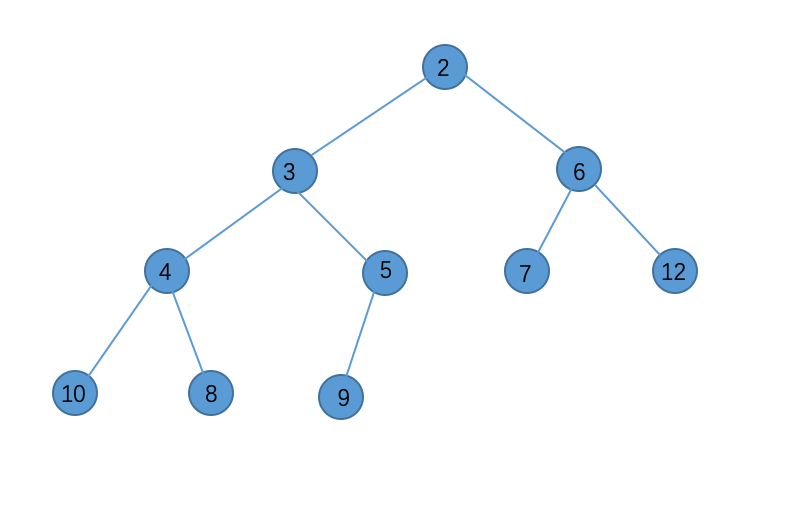
5<9，无需再交换了。

inline void pop()
{
    swap(tree[siz--],tree[1]);
    int now=1;
    while((now<<1)<=siz)
    {
        int nxt=now<<1;
        if(nxt+1<=siz&&tree[nxt+1]<tree[nxt])nxt++;
        if(tree[nxt]<tree[now])swap(tree[now],tree[nxt]);
        else break;
        now=nxt;
    }
    return;
}

4. 模板

模板题在这里

#include <iostream>
#include <cstdio>
using namespace std; 
int n,opt,x;
//------------模板开始-------------
int siz,tree[2000020];
inline int top(){return tree[1];}
inline int size(){return siz;}
inline bool empty(){return siz==0;}
inline void push(int xx)
{
    tree[++siz]=xx;
    int now=siz;
    while(now!=1)
    {
        int nxt=now>>1;
        if(tree[nxt]>tree[now])swap(tree[nxt],tree[now]);
        else break;
        now=nxt;
    }
    return;
}
inline void pop()
{
    swap(tree[siz--],tree[1]);
    int now=1;
    while((now<<1)<=siz)
    {
        int nxt=now<<1;
        if(nxt+1<=siz&&tree[nxt+1]<tree[nxt])nxt++;
        if(tree[nxt]<tree[now])swap(tree[now],tree[nxt]);
        else break;
        now=nxt;
    }
    return;
}
//------------模板结束-------------
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&opt);
		switch(opt)
		{
			case 1:
			{
				scanf("%d",&x);
				push(x);
				break;
			}
			case 2:printf("%d\n",top());break;
			case 3:pop();break;
		}
	}
	return 0;
}

4. 简单应用

1. 合并果子

这道题
简单的堆优化贪心。

#include <iostream>
#include <cstdio>
using namespace std;
int n,x,y,cnt;
//------------模板开始-------------
int siz,tree[200020];
inline int top(){return tree[1];}
inline int size(){return siz;}
inline bool empty(){return siz==0;}
inline void push(int xx)
{
    tree[++siz]=xx;
    int now=siz;
    while(now>1)
    {
        int nxt=now>>1;
        if(tree[nxt]>tree[now])swap(tree[nxt],tree[now]);
        else break;
        now=nxt;
    }
    return;
}
inline void pop()
{
    swap(tree[siz--],tree[1]);
    int now=1;
    while((now<<1)<=siz)
    {
        int nxt=now<<1;
        if(nxt+1<=siz&&tree[nxt+1]<tree[nxt])nxt++;
        if(tree[nxt]<tree[now])swap(tree[now],tree[nxt]);
        else break;
        now=nxt;
    }
    return;
}
//------------模板结束-------------
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&x);
        push(x);
    }
    for(int i=1;i<=n-1;i++)
    {
        x=top();
        pop();
        y=top();
        pop();
        cnt+=x+y;
        push(x+y);
    }
    printf("%d\n",cnt);
    return 0;
}

2. 堆排序

就是把所有的元素都放到堆里，再一个个取出。可以试试这道题。

#include <iostream>
#include <cstdio>
using namespace std; 
int n,x;
//------------模板开始-------------
int siz,tree[200020];
inline int top(){return tree[1];}
inline int size(){return siz;}
inline bool empty(){return siz==0;}
inline void push(int xx)
{
    tree[++siz]=xx;
    int now=siz;
    while(now!=1)
    {
        int nxt=now>>1;
        if(tree[nxt]>tree[now])swap(tree[nxt],tree[now]);
        else break;
        now=nxt;
    }
    return;
}
inline void pop()
{
    swap(tree[siz--],tree[1]);
    int now=1;
    while((now<<1)<=siz)
    {
        int nxt=now<<1;
        if(nxt+1<=siz&&tree[nxt+1]<tree[nxt])nxt++;
        if(tree[nxt]<tree[now])swap(tree[now],tree[nxt]);
        else break;
        now=nxt;
    }
    return;
}
//------------模板结束-------------
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&x);
		push(x);
	}
	for(int i=1;i<=n;i++)
	{
		printf("%d ",top());
		pop();
	}
	return 0;
}

上面三道题的复杂度都是\(O(n\log n)\)。

二、更多应用

1. STL priority_queue

在讲题目之前，先介绍一下STL中的优先队列。

优先队列其实就是堆……但只支持插入，删除堆顶等基础操作。

我们可以这样来定义一个大根堆：

#include <queue>//头文件
priority_queue<int> q;

小根堆麻烦一些：

#include <queue>
#include <vector>
#include <functional>
priority_queue<int,vector<int>,greater<int> > q;

对于结构体重载运算符即可。

#include <queue>
struct node{int x,y;};
bool operator <(node xx,node yy)
{
      if(xx.x!=yy.x)return xx.x<yy.x;
      return xx.y<yy.y;
}
priority_queue<node> q;

这是大根堆，小根堆只需改成这样：

#include <queue>
struct node{int x,y;};
bool operator <(node xx,node yy)
{
      if(xx.x!=yy.x)return xx.x>yy.x;
      return xx.y>yy.y;
}
priority_queue<node> q;

然后是一些基础操作：

q.push(x)//插入x
q.top()//返回堆顶
q.pop()//删除堆顶
q.empty()//是否为空
q.size()//元素个数

于是合并果子那题可以这样写：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
int n,x,y,ans;
priority_queue<int,vector<int>,greater<int> >q;
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&x);
		q.push(x);
	}
	for(int i=1;i<n;i++) 
	{
		x=q.top();q.pop();
		y=q.top();q.pop();
		ans+=x+y;
		q.push(x+y);
	}
	printf("%d\n",ans);
	return 0;
}

简洁了许多呢（笑

2. 比较复杂的模拟

舞蹈课 这道

不难想到，我们可以用堆来维护当前差距最小的一对舞者的编号。
当然你会发现一对舞者出列最多会导致两队舞者的组合被打破……
不过用一个danced数组来标记一下就行了（
那出列不还可能会多构造出一对舞者吗？
数据结构带师：套一个链表
然而我并不会懒得写，于是选择直接暴力跳
暴力跳的复杂度好像也不会炸。。。然而我不会证明>_<
u1s1这题奇怪的细节还是有的，并且数据不给下载，一出错直接爆0。。。
更多细节见代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <queue>
#include <vector>
using namespace std;
string s;
int n,cnt,a[200010];
bool danced[200010];
struct node{int x,y;};
bool operator<(node p1,node p2)//重载运算符，里面的符号是反的是因为小根堆
{
    if(abs(a[p1.x]-a[p1.y])!=abs(a[p2.x]-a[p2.y]))return abs(a[p1.x]-a[p1.y])>abs(a[p2.x]-a[p2.y]);
    else return p1.x>p2.x;
}
priority_queue<node> q;
vector<node> ans;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    cin >> n >> s;
    for(int i=0;i<n;i++)cin >> a[i];//因为string是从0开始于是就这样偷懒了（
    for(int i=1;i<s.length();i++)
        if(s[i-1]!=s[i])
            q.push((node){i-1,i});
    while(1)
    {
        while(!q.empty()&&(danced[q.top().x]||danced[q.top().y]))//如果这一对中有人danced那么直接扔掉
            q.pop();
        if(q.empty())break;//判空（防止死循环
        cnt++;//步数增加
        ans.push_back(q.top());//答案更新
        danced[q.top().x]=danced[q.top().y]=1;//标记
        int l=q.top().x,r=q.top().y;//暴力跳指针
        q.pop();//一定要记得这个时候把堆顶扔掉，要不然之后压进来又弹出去统计了个寂寞（
        while(l>=0&&danced[l])l--;//暴力跳左指针
        while(r<n&&danced[r])r++;//暴力跳右指针
        if(l>=0&&r<n&&!danced[l]&&!danced[r]&&s[l]!=s[r])q.push((node){l,r});//判断，决定是否插入
    }
    cout << cnt << endl;
    for(int i=0;i<cnt;i++)
        cout << ans[i].x+1 << ' ' << ans[i].y+1 << endl;
    return 0;
}

3. 对顶堆

黑匣子 这道

对顶堆其实就是一个小根堆倒着摞在一个大根堆上（
那这样子的话我们可以发现就整体来看元素从下往上是大致递增的

放图：

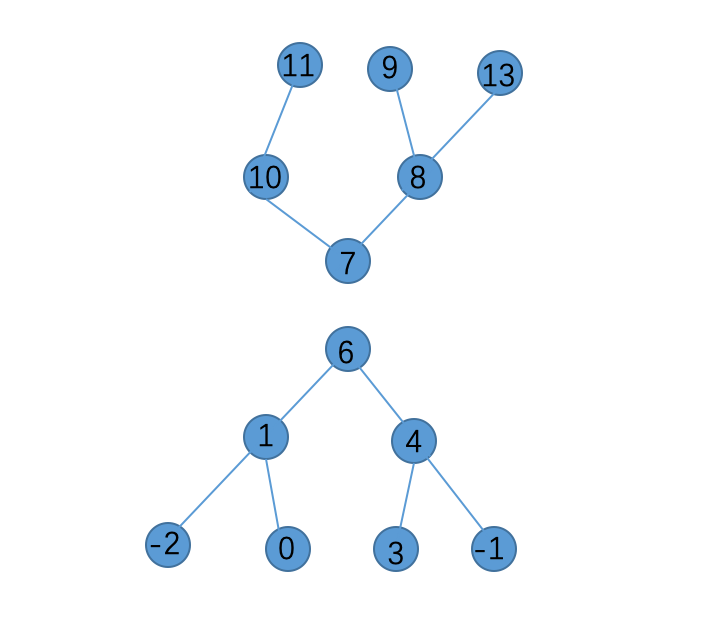
当然也可以倒着来理解，没有差别

对顶堆中两个堆的堆顶一般用来存储特殊数据。（对于这道题来说就是第i小）
插入的时候与堆顶作比较决定插入哪个堆里，然后再调整一次两个堆来让堆顶满足查询条件。
这样的话两个堆的大小差就会始终保持在正负1以内。
图就不放了（懒

一般来说每次的查询位置变动不大，这样我们才能保证对顶堆的时间复杂度正确。（也就是平衡操作的时间复杂度为\(O(1)\)）
接下来就是详细注释的代码了……

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <vector>
#include <functional>
using namespace std;
int m,n,now=1,pointer,a[200010],u[200010];
//pointer就是题目中的i……当然也可以用循环变量代替，这里它的存在就显得多余了
priority_queue<int> q1;
priority_queue<int,vector<int>,greater<int> >q2;
int main()
{
    scanf("%d%d",&m,&n);
    for(int i=1;i<=m;i++)scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)scanf("%d",&u[i]);
    for(int i=1;i<=n;i++)
    {
        pointer++;
        if(!q1.empty()&&!q2.empty()&&q1.size()<pointer)//因为pointer自增了，这里要维护一次平衡
        {
            q1.push(q2.top());
            q2.pop();
        }
        if(!q1.empty()&&!q2.empty()&&q1.size()>pointer)
        {
            q2.push(q1.top());
            q1.pop();
        }
        for(;now<=u[i];now++)
        {
            if(!q1.empty()&&a[now]>=q1.top())q2.push(a[now]);//与堆顶比较来决定插入哪个堆中
            else q1.push(a[now]);
            if(q1.size()<pointer){q1.push(q2.top());q2.pop();}
            if(q1.size()>pointer){q2.push(q1.top());q1.pop();}//维护平衡
        }
        printf("%d\n",q1.top());
    }
    return 0;
}

相信您做完这题后就能轻松AC这道了qwq

u1s1对顶堆真的不难，我也不知道为什么这几道题评分这么高（