树上的许多问题都可以用dfs序+线段树予以解决。
轻重链剖分是通过优化dfs的顺序,达到优化时间复杂度的目的。
它可以(O(nlog^2n))支持链上加,链上和还有(O(nlog n))LCA,子树加,子树和。
前置知识:dfs序,树形dp,线段树,没了。
首先给出一些定义:
重儿子:子树大小最大的儿子。只能有一个重儿子。
轻儿子:不是重儿子的儿子。
重边:连接重儿子的边。
轻边:连接轻儿子的边。
重链:重边组成的链。
举个实例:如下图,加粗的为重边,有红点的为重儿子。
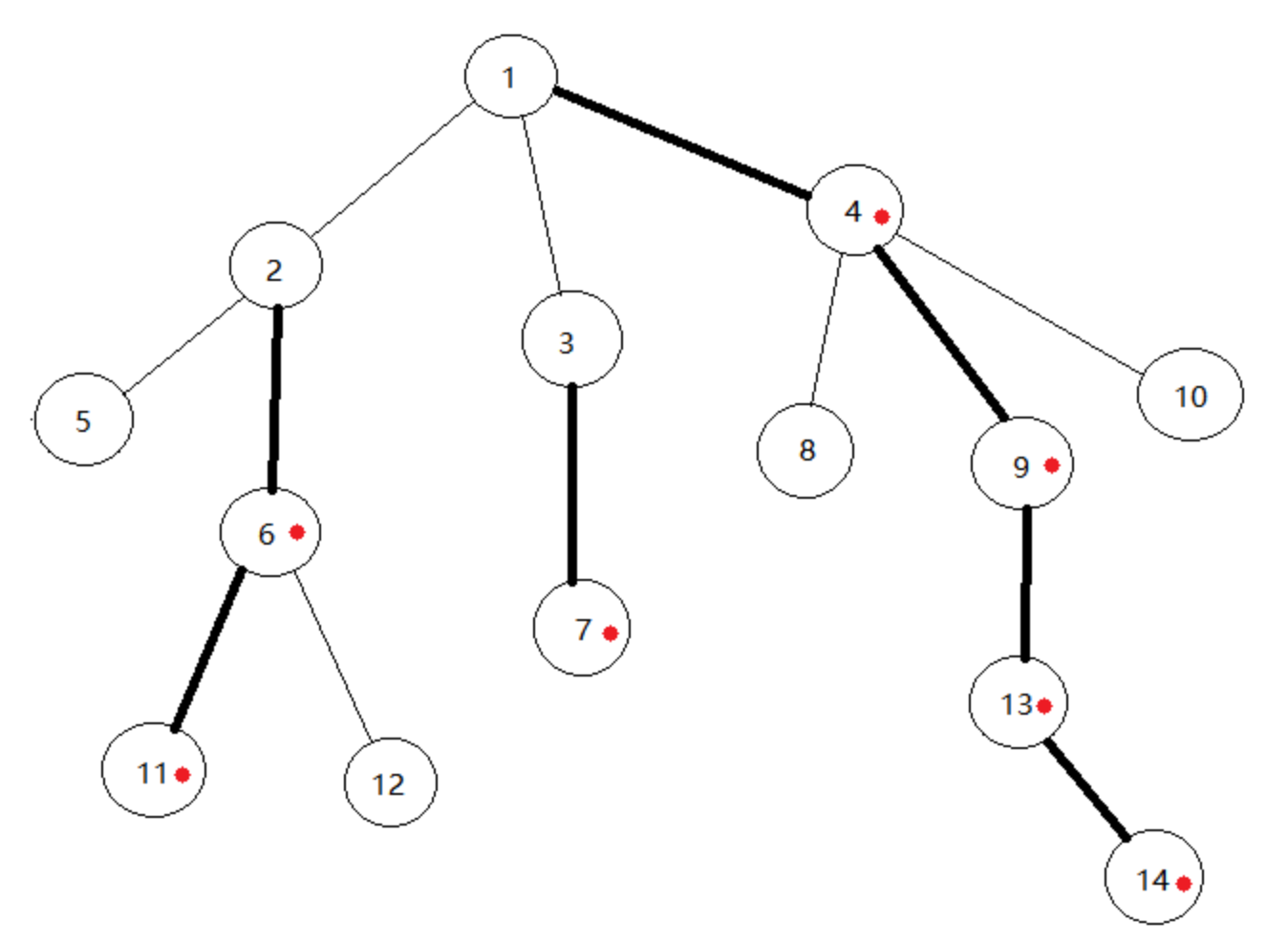
可以证明,重链的数目是(O(log n))级别的。这保证了轻重链剖分的时间复杂度。
有了重儿子有什么用?之前说过,轻重链剖分是用来优化dfs的顺序的。
在这里,我们通过优先dfs重儿子,将dfs序变得更加易处理。
但这样还不够,要支持以上的操作,我们需要记录:
- (fa[i]):(i)的父亲
- (dep[i]):(i)的深度(根节点深度为多少并不重要,不妨让根节点深度为1)
- (siz[i]):(i)的子树大小
- (son[i]):(i)的重儿子
- (top[i]):(i)所在的重链的深度最小的节点(之后简称链顶)
- (dfn[i]):(i)的dfs序
我们可以两遍dfs将这些全都求出来。第一遍dfs求出前四项,第二遍dfs求出后两项。
code:
void dfs1(int u,int f)//u为当前节点,f为u的父亲
{
fa[u]=f;siz[u]++;dep[u]=dep[f]+1;
int maxsiz=0;
for(int i=h[u];i;i=e[i].nxt)
{
int p=e[i].to;
if(p==f)continue;
dfs1(p,u);siz[u]+=siz[p];
if(maxsiz<siz[p]){maxsiz=siz[p];son[u]=p;}
}
}
void dfs2(int u,int f)//u为当前节点,f为u所在链的链顶(这与dfs1中的意义是不同的!)
{
top[u]=f;dfn[u]=++dfncnt;
if(!son[u])return;//叶节点的son[u]为0
dfs2(son[u],f);//优先dfs重儿子
for(int i=h[u];i;i=e[i].nxt)
{
int p=e[i].to;
if(p!=son[u]&&p!=fa[u])dfs2(p,p);
}
}
将结果放到刚刚的那棵树上:

可以看到,有一个很强的性质:重链上dfn连续,每一棵子树dfn连续。
这样我们就可以用线段树来维护链上和树上的加与和了。
具体操作:
子树:
void addtree(int u,int k){modify(1,dfn[u],dfn[u]+siz[u]-1,k%p);}//区间显然为[dfn[u],dfn[u]+siz[u]-1]
int querytree(int u){return query(1,dfn[u],dfn[u]+siz[u]-1);}
链:
作为引入,首先考虑如何利用轻重链剖分快速求LCA。
首先,当两个节点在一条重链上时(这个很好判断,就是看top是否相等),深度小的那个为LCA。
但要是不在一条链上呢?
每次取top的深度小的点,将这个点u跳到fa[top[u]]。
听上去比较抽象,但模拟一下就会明白。
还是刚才的图,求LCA(10,11)。
dep[top[10]]=dep[10]=3
dep[top[11]]=dep[2]=2<3
故10上跳到fa[top[10]],即4。
再次比较,dep[top[4]]=dep[1]=1<2
故11上跳到fa[top[11]],即1。
现在两点已经在同一条重链上,故LCA为深度小的,即1。
(蓝点为top,箭头表示上跳)

code:
int lca(int u,int v)
{
while(top[u]!=top[v])//重复上跳直到在同一条重链上
{
if(dep[top[u]]<dep[top[v]])swap(u,v);
u=fa[top[u]];//上跳操作
}
if(dep[u]>dep[v])swap(u,v);//已经在同一条重链上,深度小的为LCA
return u;
}
回到链上加、链上和操作。
其实和LCA一模一样,只不过要在上跳时顺便更新/统计链上的值罢了。(能这样操作得益于重链上dfn连续)
也可以看成,是将一条链拆分成了多条重链。
code:
void addpath(int u,int v,int k)
{
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])swap(u,v);
modify(1,dfn[top[u]],dfn[u],k%p);//显然top[u]的dfn更小,于是区间为[dfn[top[u]],dfn[u]]
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
modify(1,dfn[u],dfn[v],k);//最后别忘了还有一条重链
}
int querypath(int u,int v)//同上
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])swap(u,v);
ans+=query(1,dfn[top[u]],dfn[u]);ans%=p;
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
ans+=query(1,dfn[u],dfn[v]);ans%=p;
return ans;
}
这两个链上的操作因为跳链(O(log n)),线段树(O(log n)),
因此每次时间复杂度(O(log^2n)),是轻重链剖分的时间复杂度瓶颈
完整代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>
using namespace std;
const int maxn=100010;
int n,m,rt,p,cnt,dfncnt,a[maxn],w[maxn],h[maxn],dep[maxn],siz[maxn],son[maxn],fa[maxn],top[maxn],dfn[maxn];
inline int read()
{
int ret=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-f;ch=getchar();}
while(isdigit(ch)){ret=ret*10+ch-'0';ch=getchar();}
return ret*f;
}
struct node{int l,r,val,add;}tree[maxn<<2];
void pushup(int x)
{
int lson=x<<1,rson=lson|1;
tree[x].val=(tree[lson].val+tree[rson].val)%p;
}
void pushadd(int x,int k)
{
tree[x].val+=k%p*(tree[x].r-tree[x].l+1)%p;tree[x].val%=p;
tree[x].add+=k;tree[x].add%=p;
}
void pushdown(int x)
{
int lson=x<<1,rson=lson|1;
if(tree[x].l==tree[x].r)return;
if(tree[x].add!=0)
{
pushadd(lson,tree[x].add);
pushadd(rson,tree[x].add);
tree[x].add=0;
}
}
void build(int x,int l,int r)
{
tree[x]=(node){l,r,0,0};
if(l==r){tree[x].val=a[l]%p;return;}
int mid=(l+r)>>1,lson=x<<1,rson=lson|1;
build(lson,l,mid);build(rson,mid+1,r);
pushup(x);
}
void modify(int x,int l,int r,int k)
{
pushdown(x);
if(l<=tree[x].l&&r>=tree[x].r){pushadd(x,k);return;}
int mid=(tree[x].l+tree[x].r)>>1,lson=x<<1,rson=lson|1;
if(l<=mid)modify(lson,l,r,k);
if(r>mid)modify(rson,l,r,k);
pushup(x);
}
int query(int x,int l,int r)
{
pushdown(x);
if(l<=tree[x].l&&r>=tree[x].r)return tree[x].val%p;
int mid=(tree[x].l+tree[x].r)>>1,lson=x<<1,rson=lson|1,ans=0;
if(l<=mid){ans+=query(lson,l,r);ans%=p;}
if(r>mid){ans+=query(rson,l,r);ans%=p;}
return ans;
}
struct edge{int to,nxt;}e[maxn<<1];
void addedge(int u,int v){e[++cnt]=(edge){v,h[u]};h[u]=cnt;}
void add(int u,int v){addedge(u,v);addedge(v,u);}
void dfs1(int u,int f)
{
fa[u]=f;siz[u]++;dep[u]=dep[f]+1;
int maxsiz=0;
for(int i=h[u];i;i=e[i].nxt)
{
int p=e[i].to;
if(p==f)continue;
dfs1(p,u);siz[u]+=siz[p];
if(maxsiz<siz[p]){maxsiz=siz[p];son[u]=p;}
}
}
void dfs2(int u,int f)
{
top[u]=f;dfn[u]=++dfncnt;
if(w[u])modify(1,dfn[u],dfn[u],w[u]);//我个人的写法是在进行第二次dfs时处理好初始值
if(!son[u])return;
dfs2(son[u],f);
for(int i=h[u];i;i=e[i].nxt)
{
int p=e[i].to;
if(p!=son[u]&&p!=fa[u])dfs2(p,p);
}
}
int lca(int u,int v)
{
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])swap(u,v);
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
return u;
}
void addpath(int u,int v,int k)
{
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])swap(u,v);
modify(1,dfn[top[u]],dfn[u],k%p);
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
modify(1,dfn[u],dfn[v],k);
}
int querypath(int u,int v)
{
int ans=0;
while(top[u]!=top[v])
{
if(dep[top[u]]<dep[top[v]])swap(u,v);
ans+=query(1,dfn[top[u]],dfn[u]);ans%=p;
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
ans+=query(1,dfn[u],dfn[v]);ans%=p;
return ans;
}
void addtree(int u,int k){modify(1,dfn[u],dfn[u]+siz[u]-1,k%p);}
int querytree(int u){return query(1,dfn[u],dfn[u]+siz[u]-1);}
int main()
{
n=read();m=read();rt=read();p=read();
for(int i=1;i<=n;i++){int xx=read();w[i]=xx%p;}
for(int i=1;i<=n-1;i++){int uu=read(),vv=read();add(uu,vv);}
build(1,1,n);dfs1(rt,0);dfs2(rt,rt);//因为dfs2中的线段树操作,所以这里需要在dfs前先建好线段树
for(int i=1;i<=m;i++)
{
int opt=read(),x,y,z;
if(opt==1){x=read();y=read();z=read();addpath(x,y,z);}
if(opt==2){x=read();y=read();printf("%d
",querypath(x,y));}
if(opt==3){x=read();z=read();addtree(x,z);}
if(opt==4){x=read();printf("%d
",querytree(x));}
}
return 0;
}
简单的练习:
luoguP3384 【模板】轻重链剖分
luoguP4315 月下"毛景"树点权变成了边权,需要注意LCA处的处理