有向图的十字链表存储表示 以及相关操作（包括增加弧、删除弧、删除顶点等）

 

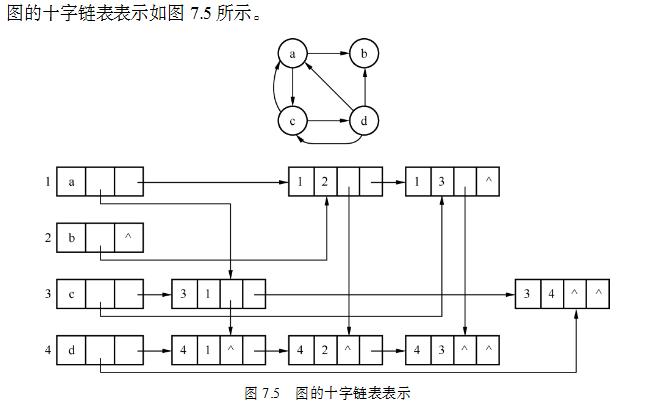
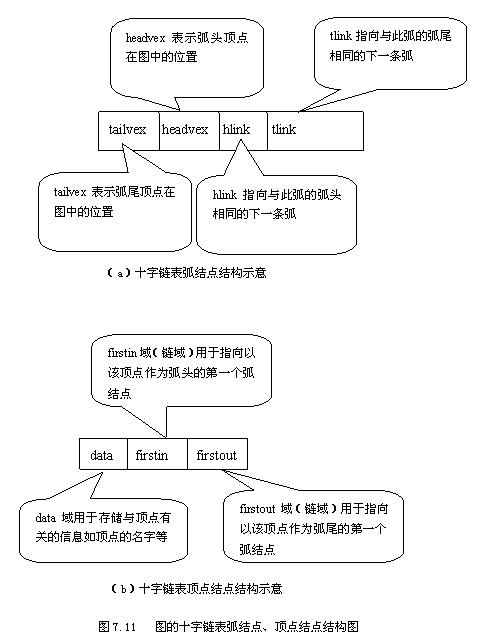
十字链表表示特点

 1.针对弧结点，增加入弧链表结构和出弧链表结构；

2.容易求得任意顶点的出度和入度，专用于有向图的操作；

3.结构实现比较复杂。

 

 

基本数据结构

 

1.弧的数据结构

typedef struct Arc
{
     int tailvex;
     int headvex;
     struct OLGArc *hlink;
     struct OLGArc *tlink;
}OLGArc;

 

2.顶点结构

typedef struct VexNode
{
     char data;
     OLGArc *firstin;
     OLGArc *firstout;
}OLGVNode;

 

3.图的十字链表表示

typedef struct
{
     OLGVNode xlist[MAX_VERTEX_NUM];
     int vexnum;
     int arcnum;
}OLGraph;

 

有向图的十字链表表示的相关操作

 

1.求图中某顶点在顶点数组中的下标

int LocateVex(OLGraph G,char x)
{
     int i;
     for(i=0;i<G.vexnum;++i)
          if(G.xlist[i].data==x)
               return i;
          return -1;
}

 

2.创建有向图的十字链表存储表示

void CreateOLGraph(OLGraph &G)
{
     int i,j,k;
     char u,v;      //printf("input vexnum of G ");
     scanf("%d",&G.vexnum);
     //printf("input arcnum of G ");
     scanf("%d",&G.arcnum);
     printf("input value of each vertex of G ");           // initial vertex array
    getchar();
     for(i=0;i<G.vexnum;++i)
     {
          scanf("%c",&G.xlist[i].data);     //such as A B C D ,There is a blank between two vertex when you input data
          if(i!=G.vexnum - 1)
               getchar();              //eat the blank
          G.xlist[i].firstin=NULL;
          G.xlist[i].firstout=NULL;
     }
     printf("input the information of arc of G ");
     for(k=0;k<G.arcnum;++k)
     {
          scanf("%c %c",&u,&v);          
          getchar();          //eat the
          i=LocateVex(G,u);
          j=LocateVex(G,v);
          OLGArc *p;
          p=(OLGArc*)malloc(sizeof(OLGArc));   // apply a new save space
          p->tailvex=i;
          p->headvex=j;
          p->hlink=G.xlist[j].firstin;
          p->tlink=G.xlist[i].firstout;
          G.xlist[i].firstout=p;
          G.xlist[j].firstin=p;
     }
}

 

3.十字链表存储表示的有向图的打印输出

void Display(OLGraph G)
{
     int i,j,k;
     OLGArc *p;
     for(i=0;i<G.vexnum;++i)
               printf("%c ",G.xlist[i].data);
     printf(" ");
     for(i=0;i<G.vexnum;++i)
     {
          for(p=G.xlist[i].firstout;p!=NULL;p=p->tlink)
               printf("%c--->%c ",G.xlist[i].data,G.xlist[p->headvex].data);
     }
     printf(" ");
}

 

4.在有向图中插入一条新的弧

void InsertArc(OLGraph &G,char u,char v)
{
     int i,j;
     OLGArc *p;
     i=LocateVex(G,u);
     j=LocateVex(G,v);
     p=(OLGArc*)malloc(sizeof(OLGArc));
     p->headvex=j;
     p->tailvex=i;
     p->hlink=G.xlist[j].firstin;
     p->tlink=G.xlist[i].firstout;
     G.xlist[i].firstout=p;
     G.xlist[j].firstin=p;
     G.arcnum++;
}

 

5.在有向图中删除一条弧

void DeleteArc(OLGraph &G,char u,char v)
{
     int i,j;
     OLGArc *p,*q;
     i=LocateVex(G,u);
     j=LocateVex(G,v);
     //修改u的出弧链表
     if(G.xlist[i].firstout->headvex==j)
     {
          q=G.xlist[i].firstout;
          G.xlist[i].firstout=q->tlink;
          G.arcnum--;
     }
     else
     {
          for(p=G.xlist[i].firstout;p&&(p->tlink!=NULL)&&(p->tlink->headvex!=j);p=p->tlink);
                    if(p&&p->tlink)       //之前没有加p->tlink!=NULL,若p->tlink==NULL，则q==NULL,q->tlink也就无意义了，同上差不多，会造成各种指针错误
                    {
                         q=p->tlink;
                         p->tlink=q->tlink;
                         G.arcnum--;
                    }
     }
     //修改v的入弧链表
     if(G.xlist[j].firstin->tailvex==i)
     {
          q=G.xlist[j].firstin;
          G.xlist[j].firstin=q->hlink;
            free(q);
     }
     else
     {
          for(p=G.xlist[j].firstin;p&&(p->hlink)&&(p->hlink->tailvex!=i);p=p->hlink);
          if(p&&p->hlink)
          {
             q=p->hlink;
             p->hlink=q->hlink;
             free(q);
          }
     }
}

6.删除有向图中的一个顶点

顶点删除分两步删除与v相关的弧

首先删除顶点v的所有入弧，这些弧结点分散于其他顶点的出弧链表中，同时也构成了顶点v的入弧链表。

在删除顶点v的入弧结点时不用维护顶点v入弧链表的连通性，但要维护该弧结点所在的其他顶点出弧链表的连通性。

void DeleteVex(OLGraph &G,char v)
{
     int k=LocateVex(G,v);
     int i,j;
     OLGArc* p=NULL;
     OLGArc* q=NULL;
     for(j=0;j<G.vexnum;j++)   //遍历所有结点的出弧链表，找到待删的弧结点(以v作为弧头结点的弧的结点)，修改每个结点的要修改处的指针，保持目标结点被删除后仍保持原有的连通性
     {
          if(G.xlist[j].firstout==NULL)  //该顶点没有出弧链表
               continue;
          else
          {
               if(G.xlist[j].firstout->headvex==k)    //出弧链表的第一个结点恰好是要删除的结点
               {
                    q=G.xlist[j].firstout;
                    G.xlist[j].firstout=q->tlink;
                    G.arcnum--;
               }
               else
               {   //遍历链表找到要删除的弧的结点，其中(p->tlink!=NULL)，之前没有加上，造成潜在隐患，若p->tlink==NULL，则p->tlink->headvex无效的引用
                    for(p=G.xlist[j].firstout;p&&(p->tlink!=NULL)&&(p->tlink->headvex!=k);p=p->tlink);
                    if(p&&p->tlink)       //之前没有加p->tlink!=NULL,若p->tlink==NULL，则q==NULL,q->tlink也就无意义了，同上差不多，会造成各种指针错误
                    {
                         q=p->tlink;
                         p->tlink=q->tlink;
                         G.arcnum--;
                    }
               }
          }
     }
  //删除v的出弧链表和入弧链表
   p=G.xlist[k].firstout;
   while(p)
   {
        q=p;
        p=p->tlink;
        free(q);
   }
     p=G.xlist[k].firstin;
   while(p)
   {
        q=p;
        p=p->hlink;
        free(q);
   }
   for(j=k+1;j<G.vexnum;j++)   //数组前移
        G.xlist[j-1]=G.xlist[j];
   G.vexnum--;    //顶点数减一
   for(j=0;j<G.vexnum;j++)
     {
          for(p=G.xlist[j].firstout;p;p=p->tlink)
          {
               if(p->tailvex>k)
                    p->tailvex--;
               if(p->headvex>k)
                    p->headvex--;
          }
     }
}

 

7.主函数

int main()
{
     OLGraph G;
     char u,v;
     CreateOLGraph(G);
     Display(G);
     printf("input newly inserted arc ");
     scanf("%c %c",&u,&v);
     InsertArc(G,u,v);
     Display(G);
     printf("input to be deleted vertex: ");
     getchar();
     scanf("%c",&u);
     DeleteVex(G,u);
     Display(G);
     printf("input to be deleted arc: ");
     getchar();
    scanf("%c %c",&u,&v);
     DeleteArc(G,u,v);
     Display(G);
     return 0;
}
//测试数据（创建有向图的十字链表）（测试数据对应于本文第一幅图）
/*
4
7
A B C D
A B
A C
C A
C D
D A
D B
D C
*/