KMP+Trie树(AC自动机将两者优点结合起来)
三者对比下:
KMP:处理1个模式串和1个文本串匹配问题(引入了一个kmp数组)
Trie树:查询n个前缀或者单词在一个字典【n个单词所组成的】里的出现问题 (引入一个特别的Trie树)
AC自动机:给定n个模式串和1个文本串,查询模式串在文本串里出现问题 (引入了在一个fail数组【即Trie树上的kmp数组】)
那么这个新引入的fail数组是什么:
看张动图就明白
摘自:大佬ppt
http://files.cnblogs.com/files/crazyacking/AC%E8%87%AA%E5%8A%A8%E6%9C%BA%E5%9F%BA%E7%A1%80%E5%85%A5%E9%97%A8.ppt
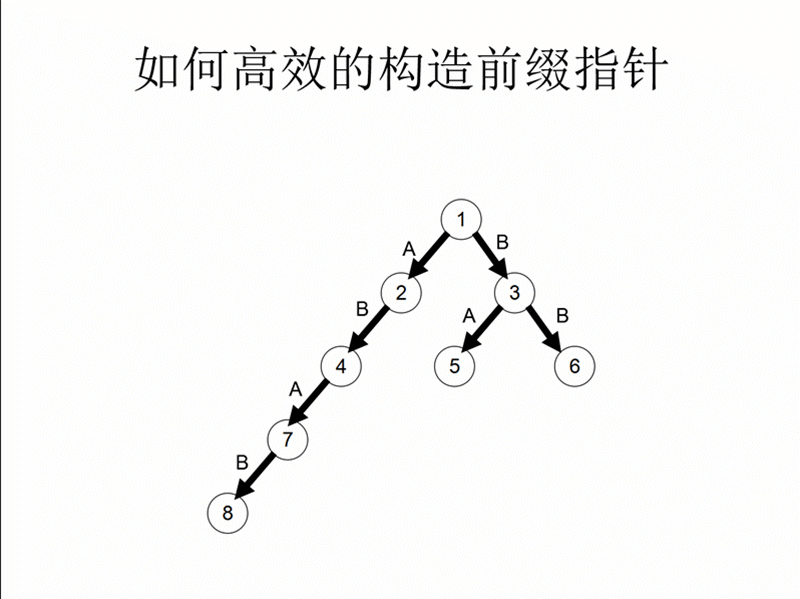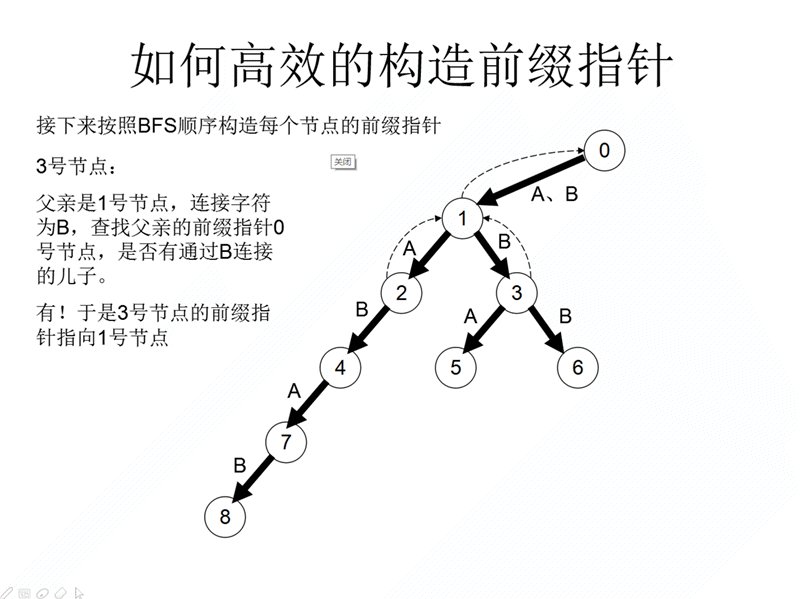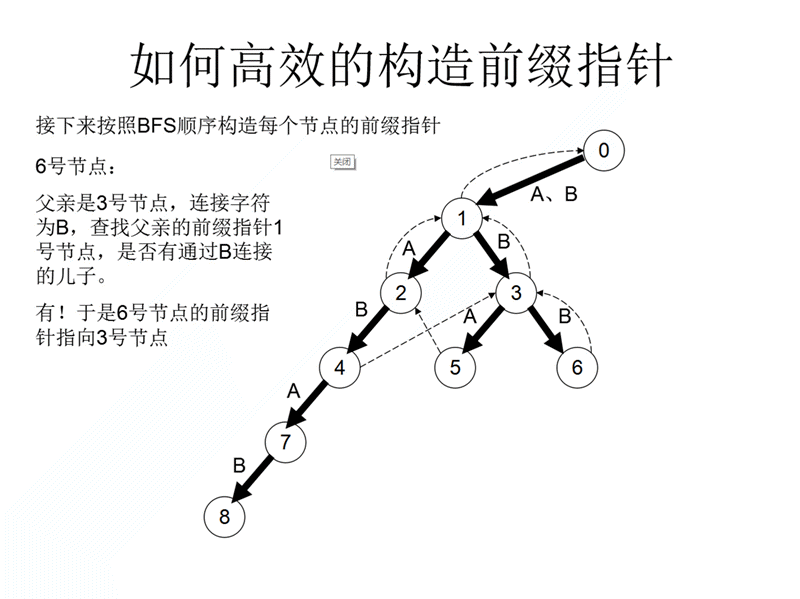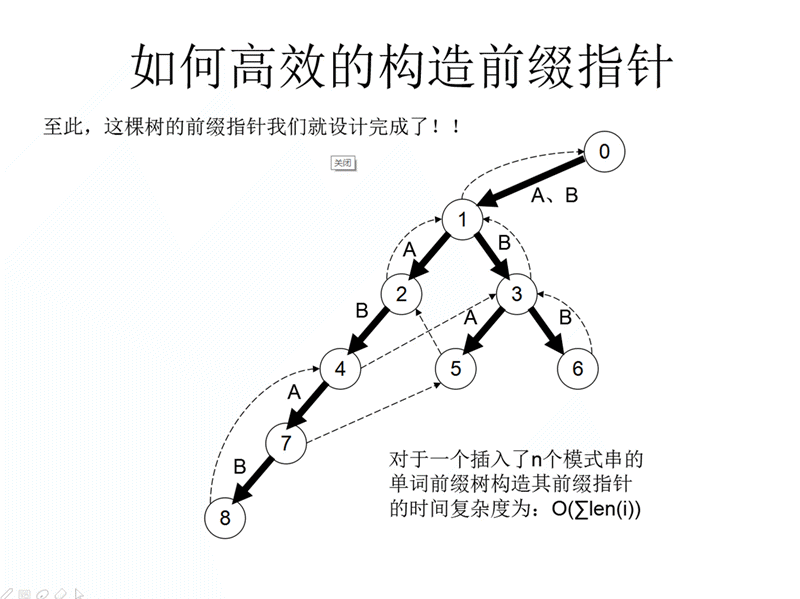
fail数组记录的是:(fa[i]是i的父节点)
假如第i号节点与fa[i]节点连边值为x,那么从fa[i]节点向上不断fa[i]=fail[fa[i]],直到发现j=fa[i]号节点存在一条与其儿子连边值为x为止,最后令fail[i]=j即可
但代码实现方式是个反的,也就是说研究对象是u=fa[i]如果发现trie[u][x]=0,那么直接赋值trie[u][x]=trie[fail[u]][x],提前上升为下面子节点服务,否则直接fail[trie[u][x]]=trie[fail[u][x]]赋值即可
AC自动机代码实现分三个部分:
void insert(char *s) //向Trie树中插入一个模式串
void build() //待所有模式串插入后,建立fail数组
int qry(char *s) //询问文本串在Trie的匹配
搬运大佬代码:
https://www.luogu.org/blog/zcysky/solution-p3808
queue<int>q; struct Tree{ int trie[N][26],sum[N],fail[N],tot=0; //插入一个模式串 void insert(char *s){ int len=strlen(s),now=0; For(i,0,len-1){ int id=s[i]-'a'; if(!trie[now][id])trie[now][id]=++tot; now=trie[now][id]; } sum[now]++; } //初始化fail数组 void build(){ For(i,0,25)if(trie[0][i])fail[trie[0][i]]=0,q.push(trie[0][i]); while(!q.empty()){ int u=q.front();q.pop(); For(i,0,25) if(trie[u][i])fail[trie[u][i]]=trie[fail[u][i]],q.push(trie[u][i]); else trie[u][i]=trie[fail[u]][i]; }} //查询 int qry(char *s){ int len=strlen(s),now=0,ans=0; For(i,0,len-1){ now=trie[now][s[i]-'a']; for(int t=now;t!=0&&~sum[t];t=fail[t]){ ans+=sum[t]; sum[t]=-1; } return ans; } }AC; main: For(i,1,n)cin>>str,AC.insert(str); AC.build(); cin>>str; cout<<AC.qry(str);