Manacher算法

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度.

摘自：

http://blog.csdn.net/dyx404514/article/details/42061017

先说一个O(n^2)复杂度解法：
根据长度奇偶性，找对称轴，奇数长度取节点，偶数取节点空隙，然后往左右两边延展匹配

Manacher算法：线性复杂度

1.为了不分奇偶两种情况，直接预处理将相邻节点间插一个"#"

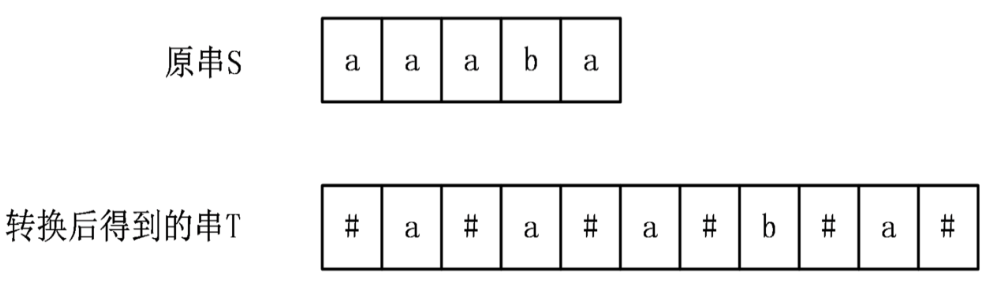
2.存一个len[i]（记录对称轴为i的向右最大长度）,那么最后要求的实际回文串长度为len[i]-1

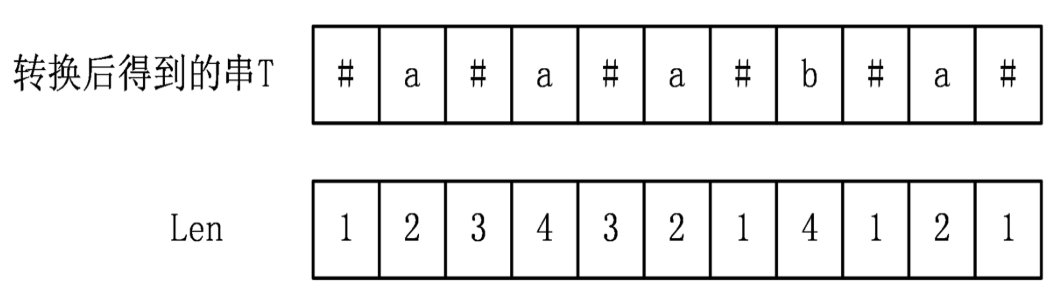
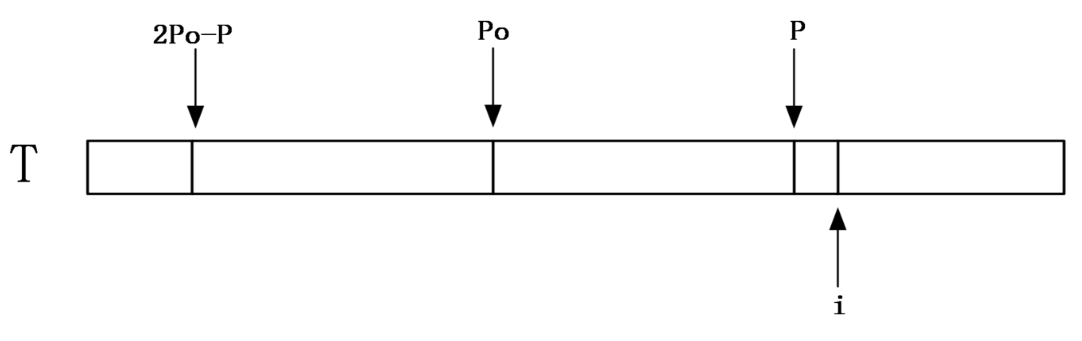
3.记忆化更新。设已处理完0 ~ i-1位置，前i个位置得出的最长回文串最右端边界位置为P，对称轴为P0。 且我们可以找到 i 关于P0 的对称点j （j<i , len[j]已知）
那么对于对称轴在i位置，分三种情况：

1. i<=P 且 i+len[j]-1<=P => len[i]=len[j]

 

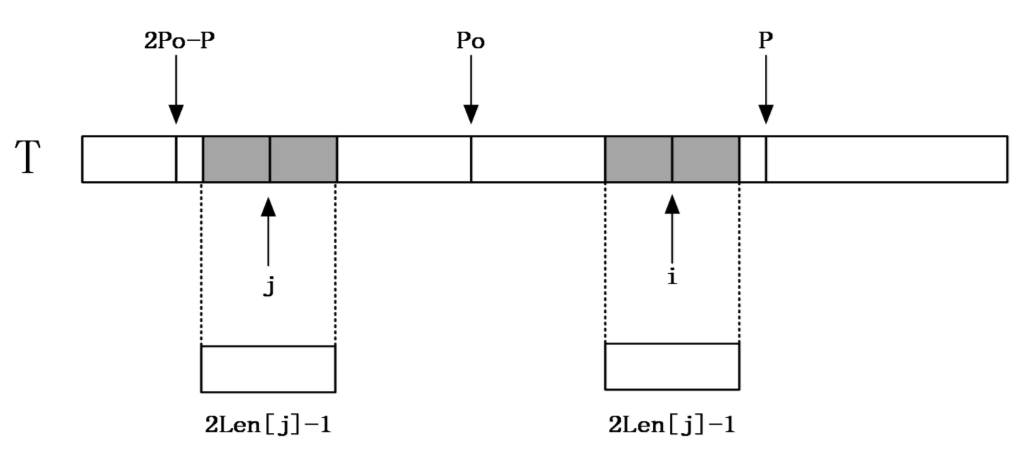
2. i<=P 且 i+len[j]-1>P => len[i]=len[j]+超出部分（手动匹配）

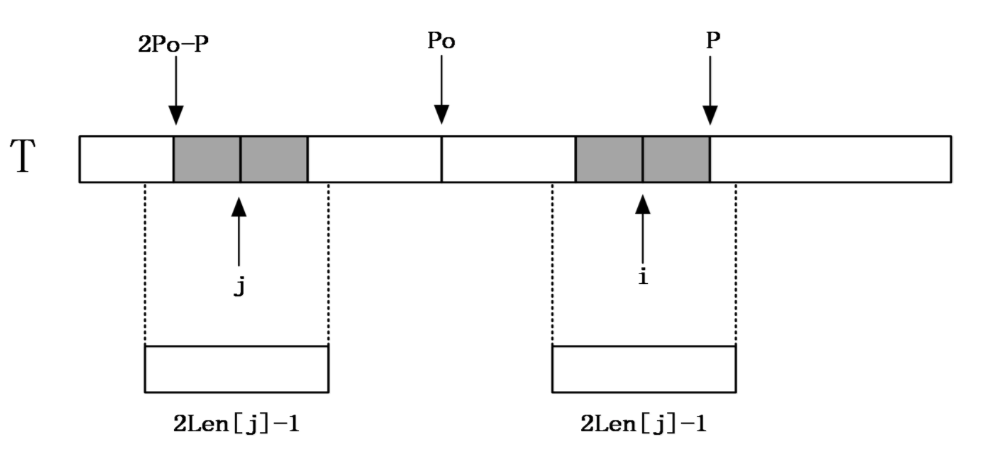
3. i>P => 完全手动匹配

 

上代码：

char str[N]; //原数组
char temp[N];//#转换后数组
int len[N];

//转换原始串
int init(char *s){
int len=strlen(s);
temp[0]='@';//防止越界
for(int i=1;i<=len*2;i+=2){
temp[i]='#';
temp[i+1]=s[i/2];
}
temp[2*len+1]='#';
temp[2*len+2]='@';//防越界
return 2*len+1;//返回转换长度
}

int manacher(char *s,int len){ //temp,2*len+1
int mx=0;//当前最大回文串右端边界位置
int ans=0,p0=0;
For(i,1,len){
int j=2*p0-i; //j关于i的对称点
if(i>mx)len[i]=1;
else len[i]=min(len[j],mx-i);
while(temp[i-len[i]]==temp[i+len[i]])len[i]++;
if(len[i]+i-1>=mx){ //记得实时更新p0,mx
mx=len[i]+i-1;
p0=i;
}
chkmax(ans,len[i]-1);
}
return ans;
}