如果两个点可以互相到达,则称为强连通。如果有向图G每个点都可以互相到达,则称为强连通图。其中G中的极大强连通子图,则称为强连通分量。
现求强连通分量是多少,且哪些点属于同一个强连通分量
tarjan由dfs,dfn[i],low[i],stack组成
dfs是遍历方式
dfn[i]:时间戳(客观上dfs遍历时每到达一个新节点序号就+1,覆盖一次就不变了)
low[i]:指原本时间戳被更小的时间戳覆盖
不多bb,看图说话:
摘自大佬博客:
https://www.cnblogs.com/shadowland/p/5872257.html
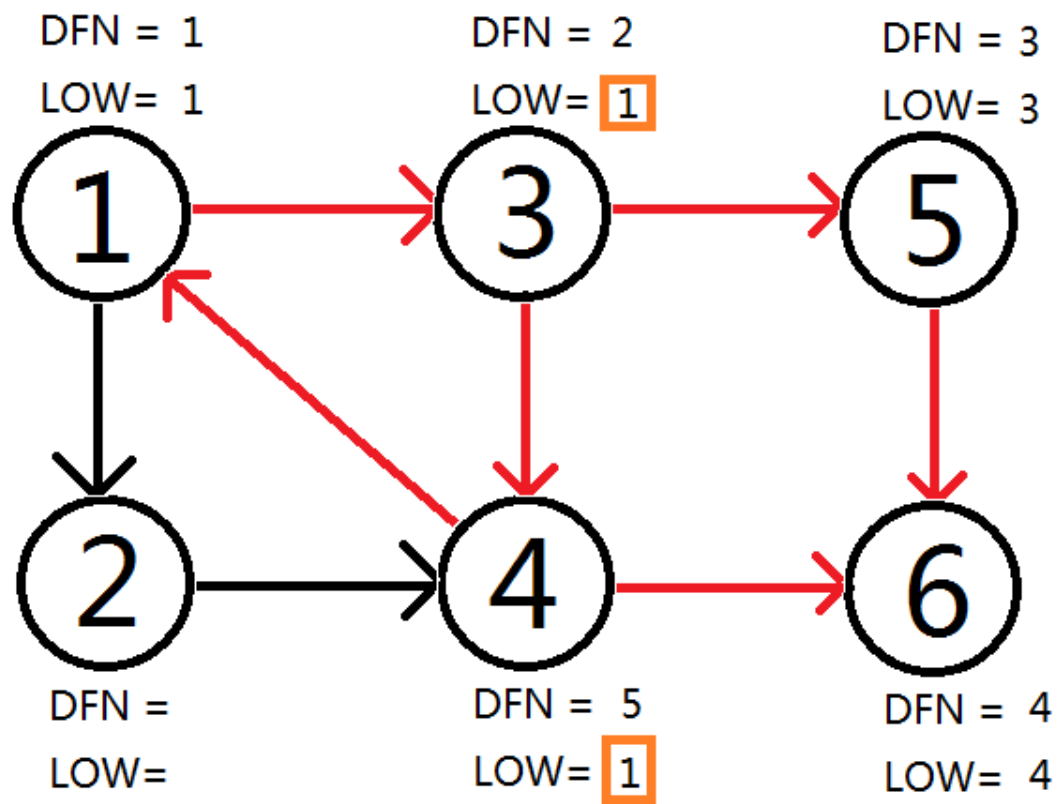
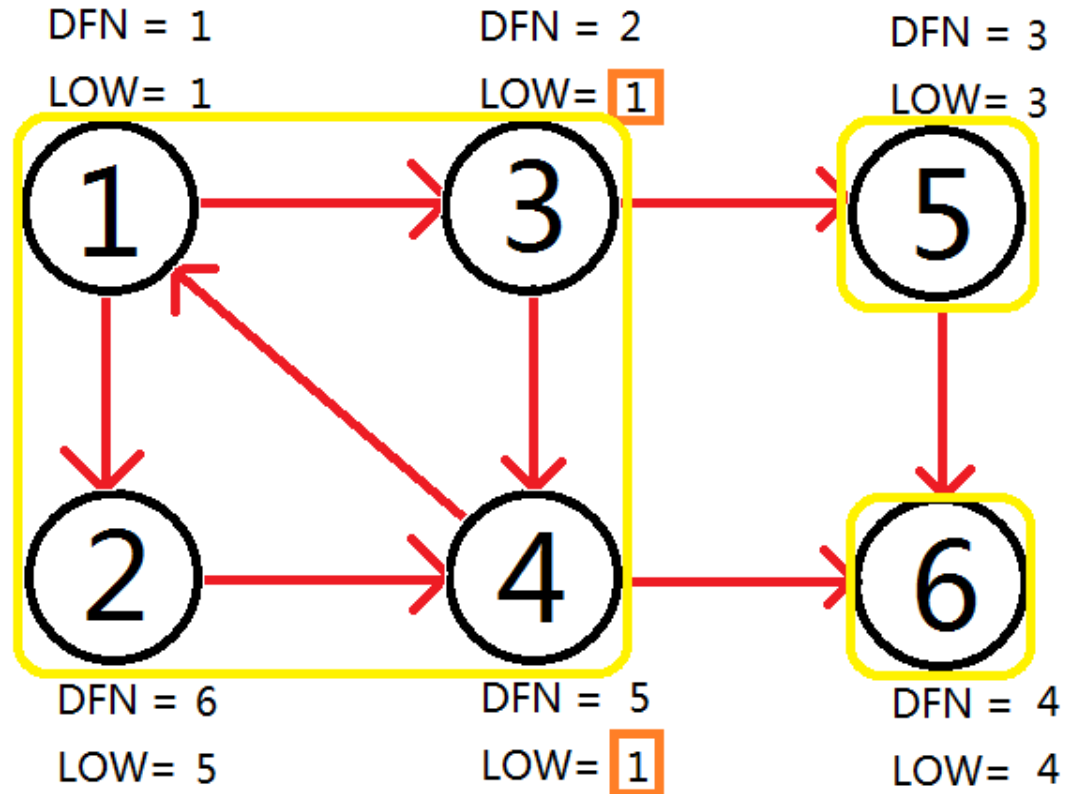
没错,若dfn[i]=low[i],那么i和i的子树(stack栈回溯实现)就构成一个强连通分量
上代码:
int idx=0;//总的dfn_num bool vis[N]; int ans=0;//总的强连通分量数 void tarjan(int u){ dfn[u]=low[u]=++tot; vis[u]=true; //判断是否在栈中 stack[++top]=x; for(i,fi[u],nx){ int v=e[i].to; if(!dfn[v])tarjan(v),chkmin(low[u],low[v]);//如果是个新节点,就dfs,回溯时记得更新low(因为是可能属于同一个强连通分量) else if(vis[v])chkmin(low[u],dfn[v]);//出现这个证明已经找到目标了,返回目标的时间戳dfn } if(dfn[u]==low[u]){//1.栈回溯,2.同一强连通分量染色,3.栈清空 ans++;
while(stack[top+1]!=u){
color[stack[top]]=ans;
vis[stack[top--]]=false; }}}
