- 对题目的思考
题目要求生成若干个已解的数独棋盘。首先想到的是遍历棋盘,找出符合数独规则的情况并。按照这种思路,从棋盘第二个空格开始,用数字1-9填充,分别判断九个数字是否满足规则(与横竖线上,九宫内的数字不重复),若满足便填入该空格并用1-9继续填充下一格,81格全部填完时输出该棋盘。可以等价为一棵除叶节点外每个节点有8个子节点的树,棋盘的每一个解都存在于一条根到叶的路径上,上述便是对该路径的遍历。 - 设计实现
依据前面的思考,构造三个主要函数:- nextSpace():跳转到下一格,调用fillSpace();
- fillSpace():调用judgement(),若满足条件便赋值给该格接着调用nextSpace();
- judgement():判断某各中某数字是否满足条件;
即递归调用上述函数实现对棋盘的遍历。
- 代码说明
void fillSpace(int r, int c)
{
for (int s = 1; s < 10; s++)//分别填入数字1-9
{
if (judgement(r, c, s))//判断是否满足条件
{
board[r][c] = s;//给该位置赋值
nextSpace(r, c);//准备填下一个位置
board[r][c] = 0;//初始化该位置
}
}
}
void nextSpace(int r, int c)
{
c++;
r += c / 9;
r = r % 9;
c = c % 9;//跳转到下一位置
fillSpace(r, c);
}
- 运行结果
部分运行结果。

结果明显的展示了这种遍历方法的结果非随机的特点。 - 性能分析
在下图性能分析的摘要信息中可以发现nextSpace这个函数运行时间很多。
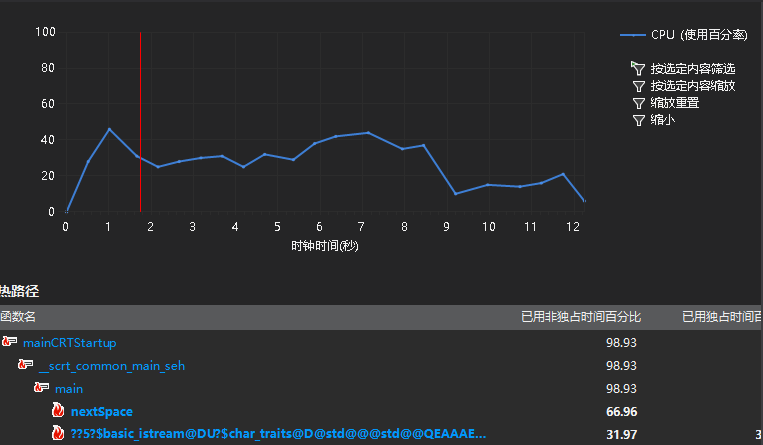
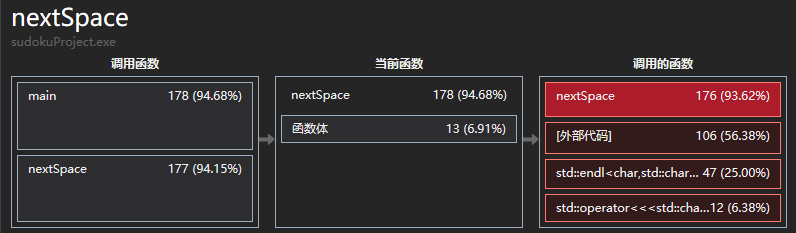
从下图调用关系树,可以发现这种算法的弊端,大规模的递归调用很占用资源并且速度很慢。
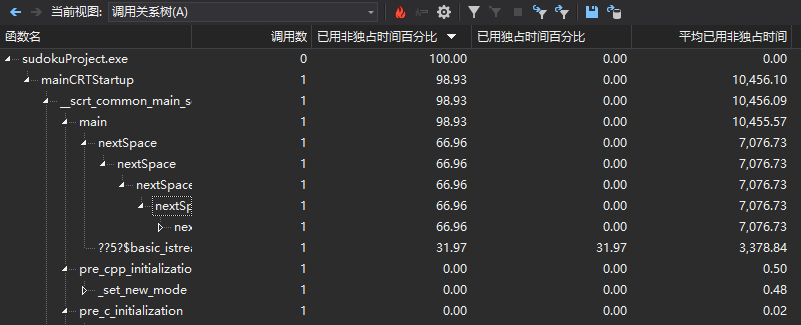
- 总结
可以看出这种利用递归遍历的方法虽然实现起来比较简单,但是效率很低。对程序的优化可以考虑利用非递归的方法实现遍利,以消除递归的弊端,目前正在思考中。
完成的任务的过程中,开始时总觉得时间很充裕,一直将任务延后,直到最后才发现时间真得很紧张,带来得后果便是完成质量的下降。我认为其原因便是没有自己的时间规划,不知不觉中时间就浪费了,觉得应该给自己规划一下。
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 690 | 810 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 300 | 200 |
| · Design Spec | · 生成设计文档 | 0 | 0 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0 | 0 |
| · Design | · 具体设计 | 60 | 80 |
| · Coding | · 具体编码 | 180 | 300 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 200 |
| Reporting | 报告 | 0 | 0 |
| · Test Report | · 测试报告 | 0 | 0 |
| · Size Measurement | · 计算工作量 | 0 | 0 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 0 | 0 |
| 合计 | 690 | 810 |