CodeForces 55D Beautiful numbers

题意：对于一个数n，如果它能被它各个数位上的除了0的数字整除，则是good number。给定区间[a, b]，问good number的数量。(a, b <= 9×10^18)

解法：首先很容易想到数位dp。至于能被一些数整除的问题，就考虑如果一个数能被a和b整除，则能被lcm(a, b)(最小公倍数)整除，而1~9的lcm为2520。然后，由于思维定势，这样之后我顺理成章地想到了用状态压缩的方法表示数x是否含有1~9，这样就妥妥地超时了....其实，最小公倍数不会超过50个，直接记录就好。于是乎，只需要一个d[20][50][2520]的数组即可。

　　　由于我第一次做数位dp的时候，看别人的题解错误理解了d数组的含义(现在很多题解都不写文字说明，在代码里稍微注释一下....真的容易理解偏差)，导致我一直以来写的非递归形式的数位dp都是效率比较低的.....而恰巧前面的几道题状态数都很少，所以就过了，而这道题如果用那种方法写出来极限数据大概要跑0.7+s，10组test就跪了......(用比较快的写法10组test最终跑出来为0.4+s)。

　　　我写的代码，定义的d[i][j][k]表示长度为i的数，它各数位的数字的最小公倍数为idx[j]，除以2520的余数是k的数一共有多少个，而速度较快的写法定义的d[i][j][k]做数位dp时扫描到第i位时，前面数字的最小公倍数为idx[j]，前面的数的余数为k时，要使最终形成的数满足题意，后面i位数总共有多少种可能。具体讲出来好像比较抽象，看代码把...我把错误代码贴出来贴在最后。

Ps:由于每次进位都会*10，所以其实可以只用保存mod 252的余数即可，具体怎么写我把NotOnlySuccess的代码贴出来。

PPs:虽然这道题浪费了很多时间....但是感觉对数位dp的理解更加到位了，也算是有所收获吧....

tag:数位dp, good

我的AC Code:

/*
 * Author:  Plumrain
 * Created Time:  
 * File Name: DP-CF-55D-2.cpp
 */
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<vector>
#include<cstdlib>
#include<sstream>
#include<fstream>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<cctype>
#include<ctime>
#include<utility>

using namespace std;

#define CLR(x) memset(x, 0, sizeof(x))
#define CLR1(x) memset(x, -1, sizeof(x))
#define PB push_back
#define SZ(v) ((int)(v).size())
#define INF 999999999999
#define zero(x) (((x)>0?(x):-(x))<eps)
#define out(x) cout<<#x<<":"<<(x)<<endl
#define tst(a) cout<<#a<<endl
#define CINBEQUICKER std::ios::sync_with_stdio(false)

const double eps = 1e-8;
const double PI = atan(1.0)*4;
const int maxint = 2147483647;
const int mod = 2520;

typedef vector<int> VI;
typedef vector<string> VS;
typedef vector<double> VD;
typedef pair<int, int> pii;
typedef long long int64;

inline int Mymod (int a, int b) {int x=a%b; if(x<0) x+=b; return x;}

int dit[20], idx[mod+5];
int64 d[20][50][mod];

inline int lcm(int a, int b)
{
    if (!a || !b) return max(a, b);
    return a / __gcd(a, b) * b;
}

int64 rec(int p, int sum, int cnt)
{
    if (p < 0) return sum % cnt == 0;
    
    int64& ret = d[p][idx[cnt]][sum];
    if (ret != -1) return ret;
    ret = 0;
    for (int i = 0; i < 10; ++ i)
        ret += rec (p-1, (sum*10+i)%mod, lcm(cnt, i));
    return ret;
}

int64 gao(int64 x)
{
    if (x < 10) return x;

    int len = 0;
    while (x){
        dit[len++] = x % 10;
        x /= 10;
    }

    int sum = 0, cnt = 1;
    int64 ret = 0;
    for (int i = len-1; i >= 0; -- i){
        for (int t = 0; t < dit[i]; ++ t)
            ret += rec(i-1, (sum*10+t)%mod, lcm(cnt,t));

        cnt = lcm(cnt, dit[i]);
        sum = (sum*10 + dit[i]) % mod;
    }
    return ret;
}

void init()
{
    CLR1 (d);
    int all = 0;
    for (int i = 1; i <= mod; ++ i)
        if (mod % i == 0) idx[i] = all++;
}

int main()
{
//    freopen("a.in","r",stdin);
//    freopen("a.out","w",stdout);
//    std::ios::sync_with_stdio(false);
    init();
    int T;
    scanf ("%d", &T);
    while (T--){
        int64 a, b;
        cin >> a >> b;
        cout << gao(b+1) - gao(a) << endl;
    }
    return 0;
}

NotOnluySuccess:

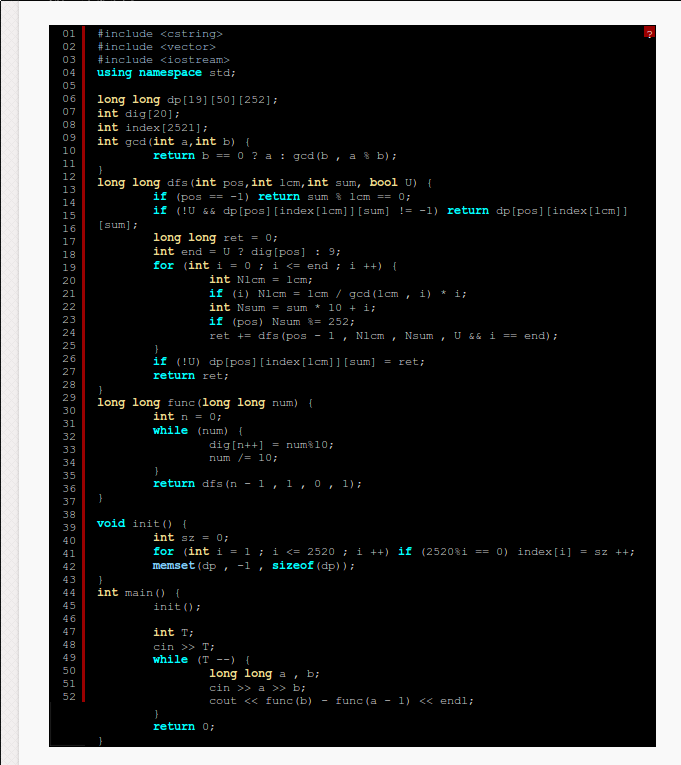
我的TLE代码(非递归)：

/*
 * Author:  Plumrain
 * Created Time:  2013-12-17 19:56
 * File Name: DP-CF-55D.cpp
 */
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstdlib>
#include <sstream>
#include <fstream>
#include <list>
#include <deque>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <bitset>
#include <cctype>
#include <ctime>
#include <utility>

using namespace std;

#define CLR(x) memset(x, 0, sizeof(x))
#define CLR1(x) memset(x, -1, sizeof(x))
#define PB push_back
#define SZ(v) ((int)(v).size())
#define ALL(t) t.begin(),t.end()
#define INF 999999999999
#define zero(x) (((x)>0?(x):-(x))<eps)
#define out(x) cout<<#x<<":"<<(x)<<endl
#define tst(a) cout<<#a<<endl
#define CINBEQUICKER std::ios::sync_with_stdio(false)

const double eps = 1e-8;
const double PI = atan(1.0)*4;
const int maxint = 2147483647;
const int N = 1 << 10;
const int mod = 2520;

typedef vector<int> VI;
typedef vector<string> VS;
typedef vector<double> VD;
typedef pair<int, int> pii;
typedef long long Int64;

inline int Mymod (int a, int b) {int x=a%b; if(x<0) x+=b; return x;}

Int64 dit[30];
Int64 ten[30], d[20][50][mod+5];
int idx[50], num[mod+1], all;

int lcm(int a, int b)
{
    if ((!a) || (!b)) return max(a, b);
    return a / __gcd(a, b) * b;
}

void init()
{
    ten[0] = 1;
    for (int i = 1; i < 19; ++ i)
        ten[i] = ten[i-1] * 10;

    CLR1 (num); CLR (idx);
    all = 0;
    for (int i = 1; i <= mod; ++ i) if (mod % i == 0){
        idx[all] = i; num[i] = all++;
    }

    CLR (d);
    d[1][0][0] = 1;
    for (int i = 1; i < 10; ++ i)
        d[1][num[i]][i] = 1;

    for (int i = 2; i < 19; ++ i){
        for (int j = 0; j < all; ++ j)
            for (int k = 0; k < mod; ++ k)
                for (int t = 0; t < 10; ++ t){
                    int tmp = lcm(t, idx[j]);
                    d[i][num[tmp]][(k*10+t)%mod] += d[i-1][j][k];
                }
    }
}

Int64 gao(Int64 x)
{
    if (x < 10) return x+1;

    int len = 0;
    while (x){
        dit[len++] = x % 10;
        x /= 10;
    }

    int flag = 0, cnt = 0;
    Int64 ret = 0;
    for (int i = len-1; i; -- i){
        for (int j = 0; j < all; ++ j)
            for (int k = 0; k < mod; ++ k)
                for (int t = 0; t < dit[i]; ++ t){
                    int tmp = lcm(t, lcm(flag, idx[j]));
                    if (((cnt + t*ten[i] + k) % tmp) == 0)
                        ret += d[i][j][k];
                }

        flag = lcm(flag, dit[i]);
        cnt = (cnt + dit[i]*ten[i]) % mod;
    }
    for (int i = 0; i <= dit[0]; ++ i)
        if (((i+cnt) % lcm(flag, i)) == 0)
            ++ ret;
    return ret;
}


int main()
{
    init();
    int T;
    scanf ("%d", &T);
    while (T--){
        Int64 a, b;
        cin >> a >> b;
        cout << gao(b) - gao(a-1) << endl;
    }
    return 0;
}