luogu P3959(2017noipTG D2T2
不知道为什么,这两天见了好多伪装成图的dp题,这道也是.
最短路只有40分,实际上可以从数据范围n<=12看出来是状压dp.
solution:
题意就是找到一种连接方法,使这些点在同一连通块中且代价最小.
因为n<=12,所以dfs+状压dp去做.
具体操作见注释.
AC码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,cnt,out[15],k,ans=1e9+7,E[15][15],dp[15][15][1<<15];
//dp[x][d][s] 点x在集合s中深度为d时的最小总代价
//目标状态为cnt==(1<<n)-1
//out[i]为层数
void work(int x,int sum,int deep)
{
//转移方程为dp[x][deep][1<<(x-1)]=min(dp[x][deep][1<<(x-1)],sum+out[i]*E[i][j])
//sum为上一层dp时的最优解,deep为层数,x为当前的集合
if(sum>=ans) return ;//剪 枝
if(x==cnt)
{
ans=sum;
return ;
}
for(int i=1;i<=n;i++)
{
if(!(1<<(i-1)&x)) continue ;
for(int j=1;j<=n;j++)
{
if(!((1<<(j-1))&x)&&E[i][j]<1e9+7)
{
if(dp[j][deep+1][1<<(j-1)|x]<=sum+out[i]*E[i][j]) continue;
dp[j][deep+1][1<<(j-1)|x]=sum+out[i]*E[i][j];
out[j]=out[i]+1;
work(1<<(j-1)|x,dp[j][deep+1][1<<(j-1)|x],deep+1);
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
cnt=(1<<n)-1;
memset(E,0x3f,sizeof(E));
while(m--)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
E[u][v]=E[v][u]=min(E[u][v],w);
// add(u,v,w);add(v,u,w);
// in[u]++;in[v]++;
// out[u]++;out[v]++;
// if(out[u]>out[v]&&out[u]>out[maxu]) maxu=u;
// if(out[v]>out[u]&&out[v]>out[maxu]) maxu=v;
// maxout=max(maxout,max(out[u],out[v]));
}
for(int i=1;i<=n;i++)
{
memset(out,0,sizeof(out));
memset(dp,0x3f,sizeof(dp));
out[i]=1;
//初始化
work(1<<(i-1),0,0);
}
printf("%d
",ans);
return 0;
}
状压dp复习:
个人认为状压最重要的就是位运算,通常情况下状压都是采用二进制压缩的(听说有三进制的,但是太菜不会)
一张关于位运算操作的图(网上找的
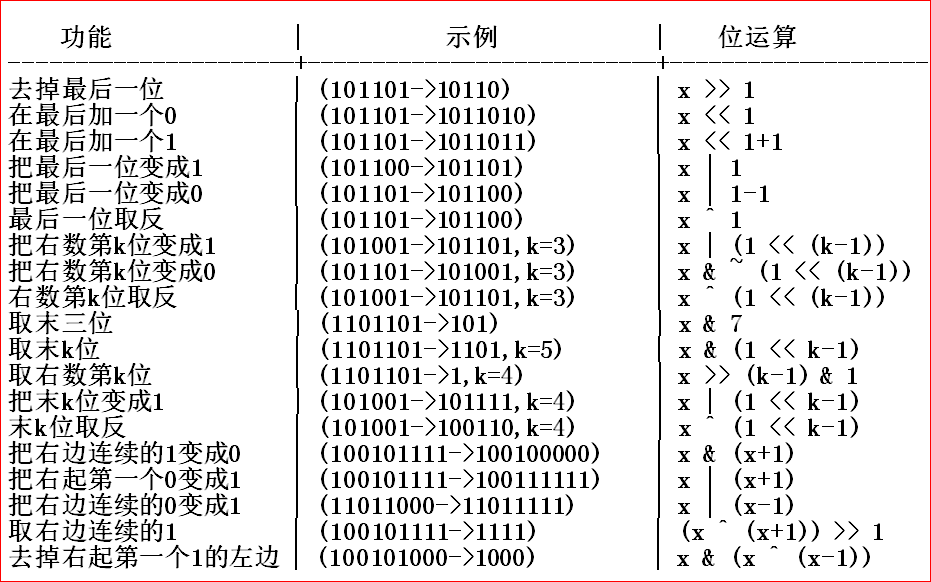
十分感谢 ___new2zy___dalao的博客,这是链接.
然后就想说一下如何选择状压dp的问题.(个人经验
通常情况下n不会超过64,一般对于每个点(步骤)存在两种情况,如:选or不选,输or赢.
其余的性质和普通dp一样(无后效性,最优,阶段)