平衡二叉树(Balanced Binary Tree)是二叉查找树的一个进化体,也是第一个引入平衡概念的二叉树。1962年,G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树,所以它又叫AVL树。平衡二叉树要求对于每一个节点来说,它的左右子树的高度之差不能超过1,如果插入或者删除一个节点使得高度之差大于1,就要进行节点之间的旋转,将二叉树重新维持在一个平衡状态。这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。

平衡二叉树实现的大部分过程和二叉查找树是一样的(学平衡二叉树之前一定要会二叉查找树),区别就在于插入和删除之后要写一个旋转算法去维持平衡,维持平衡需要借助一个节点高度的属性。
一、定义及原理
现在又a[10] = {3, 2, 1, 4, 5, 6, 7, 10, 9, 8}需要构建二叉排序树。在没有学习平衡二叉树之前,根据二叉排序树的特性,通常会将它构建成如下左图。虽然完全符合二叉排序树的定义,但是对这样高度达到8的二叉树来说,查找是非常不利的。因此,更加期望构建出如下右图的样子,高度为4的二叉排序树,这样才可以提供高效的查找效率。

平衡二叉树是一种二叉排序树,是一种高度平衡的二叉树,其中每个结点的左子树和右子树的高度至多等于1.意味着:要么是一棵空树,要么左右都是平衡二叉树,且左子树和右子树深度之绝对值不超过1. 将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF,那么平衡二叉树上的所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。
平衡二叉树的前提是它是一棵二叉排序树。
距离插入结点最近的,且平衡因子的绝对值大于1的结点为根的子树,称为最小不平衡子树。如下图所示,当插入结点37时,距离它最近的平衡因子的绝对值超过1的结点是58。

typedef struct BitNode { int data; int bf; struct BitNode *lchild, *rchild; }BitNode, *BiTree;
二、结点插入
1、插入原理
根据二叉平衡树的定义,一定保持左右子树深度绝对值小于1.在平衡二叉树插入工作一定考虑深度差,在AVL树进行插入工作时候,困难在于可能破坏AVL树的平衡属性。例如在下图
上图中插入一个节点6,那么如果不进行后续处理就会破坏树的平衡性。因为8的左子树深度为1,而右子树深度为-1.
针对此类问题,需要根据树的实际结构进行几种简单的旋转(rotation)操作就可以让树恢复AVL树的平衡性质
2.旋转问题
对于一个平衡的节点,由于任意节点最多有两个儿子,因此高度不平衡时,此节点的两颗子树的高度差2.容易看出,这种不平衡出现在下面四种情况:

1、6节点的左子树3节点高度比右子树7节点大2,左子树3节点的左子树1节点高度大于右子树4节点,这种情况成为左左。
2、6节点的左子树2节点高度比右子树7节点大2,左子树2节点的左子树1节点高度小于右子树4节点,这种情况成为左右。
3、2节点的左子树1节点高度比右子树5节点小2,右子树5节点的左子树3节点高度大于右子树6节点,这种情况成为右左。
4、2节点的左子树1节点高度比右子树4节点小2,右子树4节点的左子树3节点高度小于右子树6节点,这种情况成为右右。
从图2中可以可以看出,1和4两种情况是对称的,这两种情况的旋转算法是一致的,只需要经过一次旋转就可以达到目标,我们称之为单旋转。2和3两种情况也是对称的,这两种情况的旋转算法也是一致的,需要进行两次旋转,我们称之为双旋转。
3、旋转操作
单旋转是针对于左左和右右这两种情况的解决方案,这两种情况是对称的,只要解决了左左这种情况,右右就很好办了。图3是左左情况的解决方案,节点k2不满足平衡特性,因为它的左子树k1比右子树Z深2层,而且k1子树中,更深的一层的是k1的左子树X子树,所以属于左左情况。
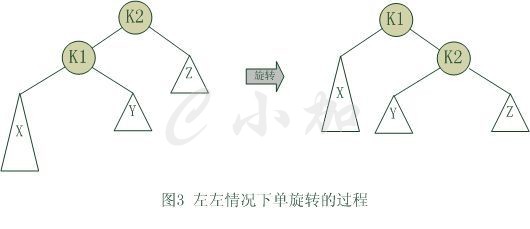
为使树恢复平衡,我们把k2变成这棵树的根节点,因为k2大于k1,把k2置于k1的右子树上,而原本在k1右子树的Y大于k1,小于k2,就把Y置于k2的左子树上,这样既满足了二叉查找树的性质,又满足了平衡二叉树的性质。
这样的操作只需要一部分指针改变,结果我们得到另外一颗二叉查找树,它是一棵AVL树,因为X向上一移动了一层,Y还停留在原来的层面上,Z向下移动了一层。整棵树的新高度和之前没有在左子树上插入的高度相同,插入操作使得X高度长高了。因此,由于这颗子树高度没有变化,所以通往根节点的路径就不需要继续旋转了。
右旋转代码
void R_rotate(BiTree *t) { BiTree s; s = (*t)->lchild; //s指向t的左子树根结点 (*t)->lchild = s->rchild; //s的右子树挂接为t的左子树 s->rchild = (*t); *t = s; //t指向新的根结点 }
右旋转原理:获取失去平衡结点以及左结点,为了让lchild作为根节点,将lchild的rchild挂接到之前左结点上,然后在挂接到s->rchild.
左旋转代码
void L_rotate(BiTree *t) { BiTree s; s = (*t)->rchild; //s指向t的右子树根结点 (*t)->rchild = s->lchild; //s的左子树挂接为t的右子树 s->lchild = (*t); *t = s; //t指向新的根结点 }
左旋转原理正好相反,让其右结点作为根节点
第六步:双旋转
对于左右和右左这两种情况,单旋转不能使它达到一个平衡状态,要经过两次旋转。双旋转是针对于这两种情况的解决方案,同样的,这样两种情况也是对称的,只要解决了左右这种情况,右左就很好办了。图4是左右情况的解决方案,节点k3不满足平衡特性,因为它的左子树k1比右子树Z深2层,而且k1子树中,更深的一层的是k1的右子树k2子树,所以属于左右情况。

为使树恢复平衡,我们需要进行两步,第一步,把k1作为根,进行一次z左旋转,旋转之后就变成了左左情况,所以第二步再进行一次右旋转,最后得到了一棵以k2为根的平衡二叉树树。
3、旋转代码分析
#define LH +1 /* 左高 */ #define EH 0 /* 等高 */ #define RH -1 /* 右高 */ /* 对以指针T所指结点为根的二叉树作左平衡旋转处理 */ /* 本算法结束时,指针T指向新的根结点 */ void LeftBalance(BiTree *T) { BiTree L,Lr; L = (*T)->lchild; /* L指向T的左子树根结点 */ switch(L->bf) { /* 检查T的左子树的平衡度,并作相应平衡处理 */ case LH: /* 新结点插入在T的左孩子的左子树上,要作单右旋处理 */ (*T)->bf=L->bf=EH; R_Rotate(T); break; case RH: /* 新结点插入在T的左孩子的右子树上,要作双旋处理 */ Lr=L->rchild; /* Lr指向T的左孩子的右子树根 */ switch(Lr->bf) { /* 修改T及其左孩子的平衡因子 */ case LH: (*T)->bf=RH; L->bf=EH; break; case EH: (*T)->bf=L->bf=EH; break; case RH: (*T)->bf=EH; L->bf=LH; break; } Lr->bf=EH; L_Rotate(&(*T)->lchild); /* 对T的左子树作左旋平衡处理 */ R_Rotate(T); /* 对T作右旋平衡处理 */ } }
首先,定义三个常数变量,分别代码1、0、-1。
(1)函数被调用,传入一个需调整平衡型的子树T,根节点为k3,由于LeftBalance函数被调用时,其实是已经确认当前子树是不平衡的状态,且左子树的高度大于右子树的高度。换句话说,此时T的根结点应该是平衡因子BF的值大于1的数。k3的BF为2
(2)将T的左孩子赋值给L。L指向K1.
(3)然后是分支判断。
(4)当L(k1)的平衡因子为LH,即为1时,表明它与根结点的BF值符号相同,因此,将它们的BF值都改为0,并进行右旋(顺时针)操作,是左左情况
(5)当L的平衡因子为RH时,即为-1时,表明它与根结点的BF值符号相反,此时需要做双旋操作。针对L的右孩子k2的BF作判断,修改结点T(k3)和L(k1)的BF值。将当前的Lr的BF改为0。从图中看到K2的左结点是连接到K1的右子树上,右结点连接到K3的左子树
其中当k2结点为RH,说明K2有右结点有,左结点无,k3为0((*T)->bf=EH; ),k1就没有右结点为LH。当为Lh看程序。
(6)对根结点的左子树进行左旋,以K1为根节点进行左旋转,形成左左情况。
(7)对根结点K3进行右旋,完成平衡操作。
三、总体代码
<strong>#include <stdio.h> #include <stdlib.h> #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 #define MAXSIZE 100 /* 存储空间初始分配量 */ typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */ /* 二叉树的二叉链表结点结构定义 */ typedef struct BitNode /* 结点结构 */ { int data; /* 结点数据 */ int bf; /* 结点的平衡因子 */ struct BitNode *lchild, *rchild; /* 左右孩子指针 */ } BitNode, *BiTree; /* 对以p为根的二叉排序树作右旋处理 */ /* 处理之后p指向新的树根结点,即旋转处理之前的左子树的根结点 */ //右旋-顺时针旋转(如LL型就得对根结点做该旋转) void R_Rotate(BiTree *P) { BiTree L; L=(*P)->lchild; /* L指向P的左子树根结点 */ (*P)->lchild=L->rchild; /* L的右子树挂接为P的左子树 */ L->rchild=(*P); *P=L; /* P指向新的根结点 */ } /* 对以P为根的二叉排序树作左旋处理, */ /* 处理之后P指向新的树根结点,即旋转处理之前的右子树的根结点0 */ //左旋-逆时针旋转(如RR型就得对根结点做该旋转) void L_Rotate(BiTree *P) { BiTree R; R = (*P)->rchild; /* R指向P的右子树根结点 */ (*P)->rchild = R->lchild; /* R的左子树挂接为P的右子树 */ R->lchild = (*P); *P = R; /* P指向新的根结点 */ } #define LH +1 /* 左高 */ #define EH 0 /* 等高 */ #define RH -1 /* 右高 */ /* 对以指针T所指结点为根的二叉树作左平衡旋转处理 */ /* 本算法结束时,指针T指向新的根结点 */ void LeftBalance(BiTree *T) { BiTree L,Lr; L = (*T)->lchild; /* L指向T的左子树根结点 */ switch(L->bf) { /* 检查T的左子树的平衡度,并作相应平衡处理 */ case LH: /* 新结点插入在T的左孩子的左子树上,要作单右旋处理 */ (*T)->bf=L->bf=EH; R_Rotate(T); break; case RH: /* 新结点插入在T的左孩子的右子树上,要作双旋处理 */ // Lr=L->rchild; /* Lr指向T的左孩子的右子树根 */ switch(Lr->bf) { /* 修改T及其左孩子的平衡因子 */ case LH: (*T)->bf=RH; L->bf=EH; break; case EH: (*T)->bf=L->bf=EH; break; case RH: (*T)->bf=EH; L->bf=LH; break; } Lr->bf=EH; L_Rotate(&(*T)->lchild); /* 对T的左子树作左旋平衡处理 */ R_Rotate(T); /* 对T作右旋平衡处理 */ } } /* 对以指针T所指结点为根的二叉树作右平衡旋转处理, */ /* 本算法结束时,指针T指向新的根结点 */ void RightBalance(BiTree *T) { BiTree R,Rl; R=(*T)->rchild; /* R指向T的右子树根结点 */ switch(R->bf) { /* 检查T的右子树的平衡度,并作相应平衡处理 */ case RH: /* 新结点插入在T的右孩子的右子树上,要作单左旋处理 */ (*T)->bf=R->bf=EH; L_Rotate(T); break; case LH: /* 新结点插入在T的右孩子的左子树上,要作双旋处理 */ //最小不平衡树的根结点为负,其右孩子为正 Rl=R->lchild; /* Rl指向T的右孩子的左子树根 */ switch(Rl->bf) { /* 修改T及其右孩子的平衡因子 */ case RH: (*T)->bf=LH; R->bf=EH; break; case EH: (*T)->bf=R->bf=EH; break; case LH: (*T)->bf=EH; R->bf=RH; break; } Rl->bf=EH; R_Rotate(&(*T)->rchild); /* 对T的右子树作右旋平衡处理 */ L_Rotate(T); /* 对T作左旋平衡处理 */ } } /* 若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个 */ /* 数据元素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树 */ /* 失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。 */ Status InsertAVL(BiTree *T,int e,Status *taller) { if(!*T) { /* 插入新结点,树“长高”,置taller为TRUE */ *T=(BiTree)malloc(sizeof(BitNode)); (*T)->data=e; (*T)->lchild=(*T)->rchild=NULL; (*T)->bf=EH; *taller=TRUE; } else { if (e==(*T)->data) { /* 树中已存在和e有相同关键字的结点则不再插入 */ *taller=FALSE; return FALSE; } if (e<(*T)->data) { /* 应继续在T的左子树中进行搜索 */ if(!InsertAVL(&(*T)->lchild, e, taller)) /* 未插入 */ return FALSE; if(*taller) /* 已插入到T的左子树中且左子树“长高” */ switch((*T)->bf) /* 检查T的平衡度 */ { case LH: /* 原本左子树比右子树高,需要作左平衡处理 */ LeftBalance(T); *taller=FALSE; break; case EH: /* 原本左、右子树等高,现因左子树增高而使树增高 */ (*T)->bf=LH; *taller=TRUE; break; case RH: /* 原本右子树比左子树高,现左、右子树等高 */ (*T)->bf=EH; *taller=FALSE; break; } } else { /* 应继续在T的右子树中进行搜索 */ if(!InsertAVL(&(*T)->rchild,e, taller)) /* 未插入 */ { return FALSE; } if(*taller) /* 已插入到T的右子树且右子树“长高” */ { switch((*T)->bf) /* 检查T的平衡度 */ { case LH: /* 原本左子树比右子树高,现左、右子树等高 */ (*T)->bf=EH; *taller=FALSE; break; case EH: /* 原本左、右子树等高,现因右子树增高而使树增高 */ (*T)->bf=RH; *taller=TRUE; break; case RH: /* 原本右子树比左子树高,需要作右平衡处理 */ RightBalance(T); *taller=FALSE; break; } } } } return TRUE; } /* 若在平衡的二叉排序树t中存在和e有相同关键字的结点,则删除之 并返回TRUE,否则返回FALSE。若因删除而使二叉排序树 失去平衡,则作平衡旋转处理,布尔变量shorter反映t变矮与否 */ int deleteAVL(BiTree *t, int key, int *shorter) { if(*t == NULL) //不存在该元素 { return FALSE; //删除失败 } else if(key == (*t)->data) //找到元素结点 { BitNode *q = NULL; if((*t)->lchild == NULL) //左子树为空 { q = (*t); (*t) = (*t)->rchild; free(q); *shorter = TRUE; } else if((*t)->rchild == NULL) //右子树为空 { q = (*t); (*t) = (*t)->lchild; free(q); *shorter = TRUE; } else //左右子树都存在, { q = (*t)->lchild; while(q->rchild) { q = q->rchild; } (*t)->data = q->data; deleteAVL(&(*t)->lchild, q->data, shorter); //在左子树中递归删除前驱结点 } } else if(key < (*t)->data) //左子树中继续查找 { if(!deleteAVL(&(*t)->lchild, key, shorter)) { return FALSE; } if(*shorter) { switch((*t)->bf) { case LH: (*t)->bf = EH; *shorter = TRUE; break; case EH: (*t)->bf = RH; *shorter = FALSE; break; case RH: RightBalance(&(*t)); //右平衡处理 if((*t)->rchild->bf == EH) //注意这里,画图思考一下 *shorter = FALSE; else *shorter = TRUE; break; } } } else //右子树中继续查找 { if(!deleteAVL(&(*t)->rchild, key, shorter)) { return FALSE; } if(shorter) { switch((*t)->bf) { case LH: LeftBalance(&(*t)); //左平衡处理 if((*t)->lchild->bf == EH) //注意这里,画图思考一下 *shorter = FALSE; else *shorter = TRUE; break; case EH: (*t)->bf = LH; *shorter = FALSE; break; case RH: (*t)->bf = EH; *shorter = TRUE; break; } } } return TRUE; } void InOrderTraverse(BiTree t) { if(t) { InOrderTraverse(t->lchild); printf("%d ", t->data); InOrderTraverse(t->rchild); } } int main(void) { int i; int a[10]={3,2,1,4,5,6,7,10,9,8}; BiTree T=NULL; Status taller; for(i=0;i<10;i++) { InsertAVL(&T,a[i],&taller); } printf("中序遍历二叉平衡树: "); InOrderTraverse(T); printf(" "); printf("删除结点元素5后中序遍历: "); int shorter; deleteAVL(&T, 5, &shorter); InOrderTraverse(T); printf(" "); return 0; }
